
Урок «Неравенства с двумя переменными»

Краткое описание документа:
Видеоурок «Неравенства с двумя переменными» предназначен для обучения алгебре по данной теме в 9 классе общеобразовательной школы. Видеоурок содержит описание теоретических основ решения неравенств, подробно описывает процесс решения неравенств графическим способом, его особенности, демонстрирует примеры решения заданий по теме. Задача данного видеоурока – при помощи наглядного представления информации облегчить понимание материала, способствовать формированию умений в решении задач с применением изученных математических методов.
Основными инструментами видеоурока являются использование анимации в представлении графиков и теоретических сведений, выделение понятий, особенностей, важных для понимания и запоминания материала, цветом и другими графическими способами, голосовое сопровождение объяснения с целью более легкого запоминания информации и формирования умения использования математического языка.

Видеоурок начинается и представления темы и примера, демонстрирующего понятие решения неравенства. Для формирования понимания смысла понятия решения представлено неравенство 3х2-у<10, в которое подставляется пара значений х=2 и у=6. Демонстрируется, как после подстановки данных значений неравенство становится верным. Понятие решения данного неравенства как пары значений (2;6) выведено на экран, подчеркивая его важность. Затем представляется определение рассмотренного понятия для запоминания его учениками или записи в тетрадь.
Важной частью умения решать неравенства является умение изобразить на координатной плоскости множество его решений. Формирование такого умения в данном уроке начинается с демонстрации нахождения множества решений линейных неравенств ax+by<c и ax+by>c. Отмечаются особенности задания неравенства – х и у являются переменными, a, b, c – некоторыми числами, среди которых a и b не равны нулю.
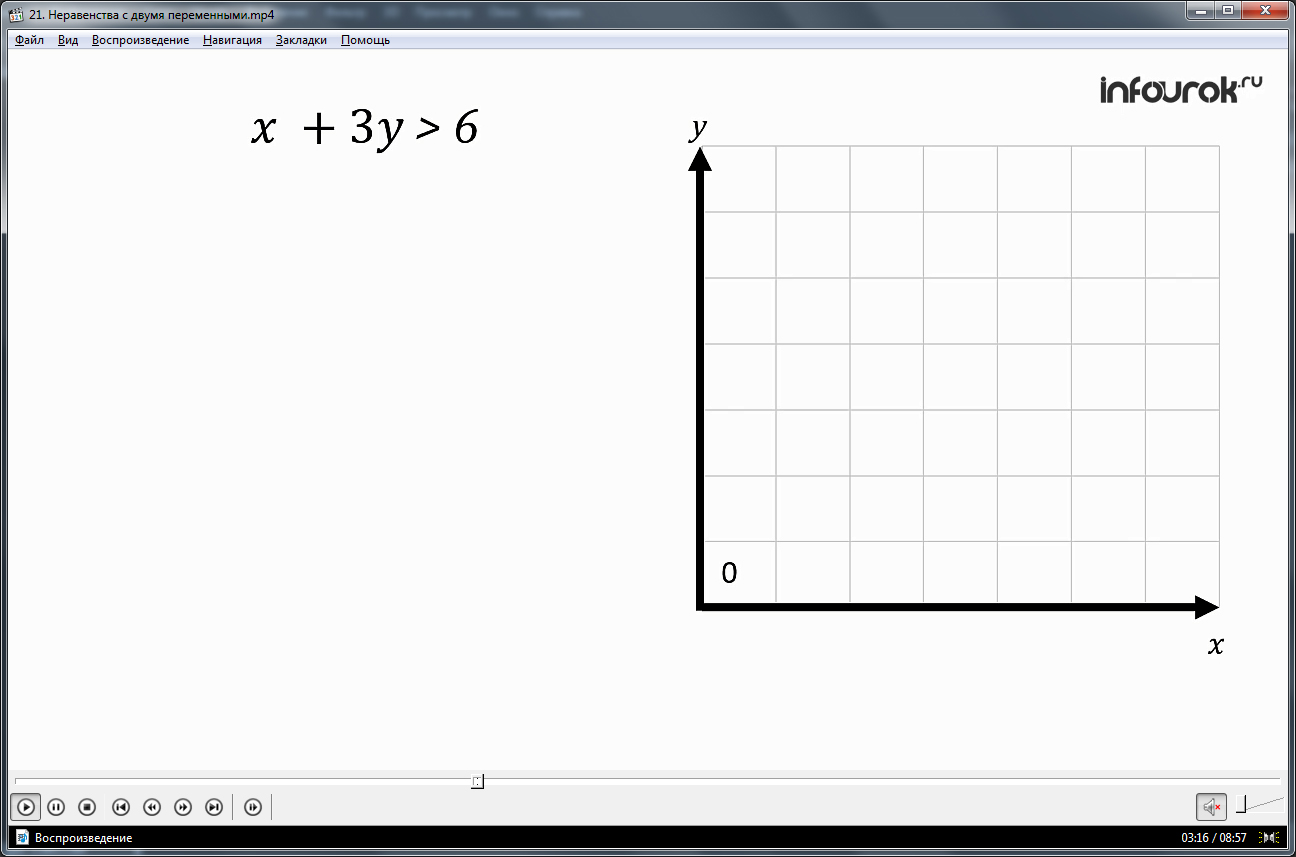
Примером такого неравенства является х+3у>6. Чтобы преобразовать неравенство в равносильное неравенство, отражающее зависимость значений у от значений х, обе части неравенства делятся на 3, у остается в одной части уравнения, а х переносится в другую. Произвольно выбирается значение х=3 для подстановки в неравенство. Отмечается, что данное значение х подставить в неравенство и заменить знак неравенства знаком равенства, можно найти соответствующее значение у=1. Пара (3;1) будет являться решением уравнения у=-(1/3)х+2. Если же подставлять любые значения у, большие 1, то неравенство с данным значением х будет верно: (3;2), (3;8) и др. Аналогично данному процессу нахождения решения рассматривается общий случай для поиска множества решений данного неравенства. Поиск множества решений неравенства начинается с подстановки некоторого значения х0. В правой части неравенства получается выражение –(1/3)х0+2. Некоторая пара чисел (х0;у0) является решением уравнения у=–(1/3)х+2. Соответственно решениями неравенства у>–(1/3)х0+2 будут соответствующие пары значений с х0, где у больше значений у0. То есть решениями этого неравенства будут пары значений (х0;у).
Чтобы найти на координатной плоскости множество решений неравенства х+3у>6, на ней демонстрируется построение прямой, соответствующей уравнению у=-(1/3)х+2. На данной прямой отмечается точка М с координатами (х0;у0). При этом отмечается, что все точки К(х0;у) с ординатами у>у0, то есть расположенные выше данной прямой, будут удовлетворять условиям неравенства у>-(1/3)х+2. Из анализа делается вывод о том, что данным неравенство задается множество точек, которые располагаются выше прямой у=-(1/3)х+2. Это множество точек составляют полуплоскость над данной прямой. Так как неравенство строгое, сама прямая не входит в число решений. На рисунке данный факт отмечен пунктирным обозначением.
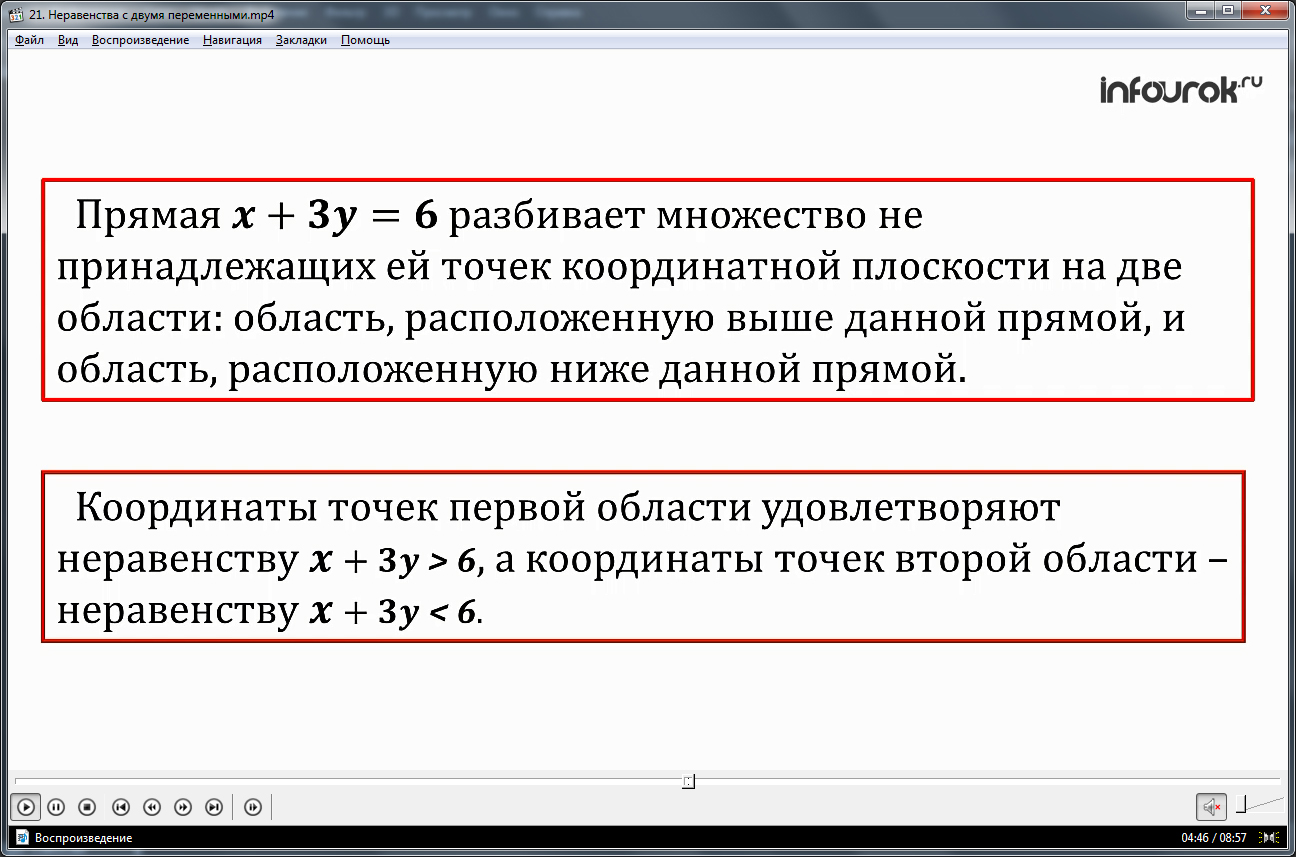
Обобщая данные, полученные в результате описания решения неравенства х+3у>6, можно говорить о том, что прямая х+3у=6 разбивается плоскость на две полуплоскости, при этом расположенная выше полуплоскость отражает множество значений удовлетворяющих неравенству х+3у>6, а распложенная ниже прямой – решение неравенства х+3у<6. Данный вывод является важным для понимания, каким образом решаются неравенства, поэтому выведен на экран отдельно в рамке.
Далее рассматривается пример решения нестрогого неравенства второй степени у>=(х-3)2. Для определения множества решений рядом на рисунке строится парабола у=(х-3)2. На параболе отмечается точка М(х0;у0), значения которой будут решениями уравнения у=(х-3)2. В данной точке строится перпендикуляр, на котором выше параболы отмечается точка К(х0;у), которая будет решением неравенства у>(х-3)2. Можно сделать вывод о том, что исходному неравенству удовлетворяют координаты точек, расположенных на данной параболе у=(х-3)2 и выше ее. На рисунке данную область решений отмечают штрихованием.
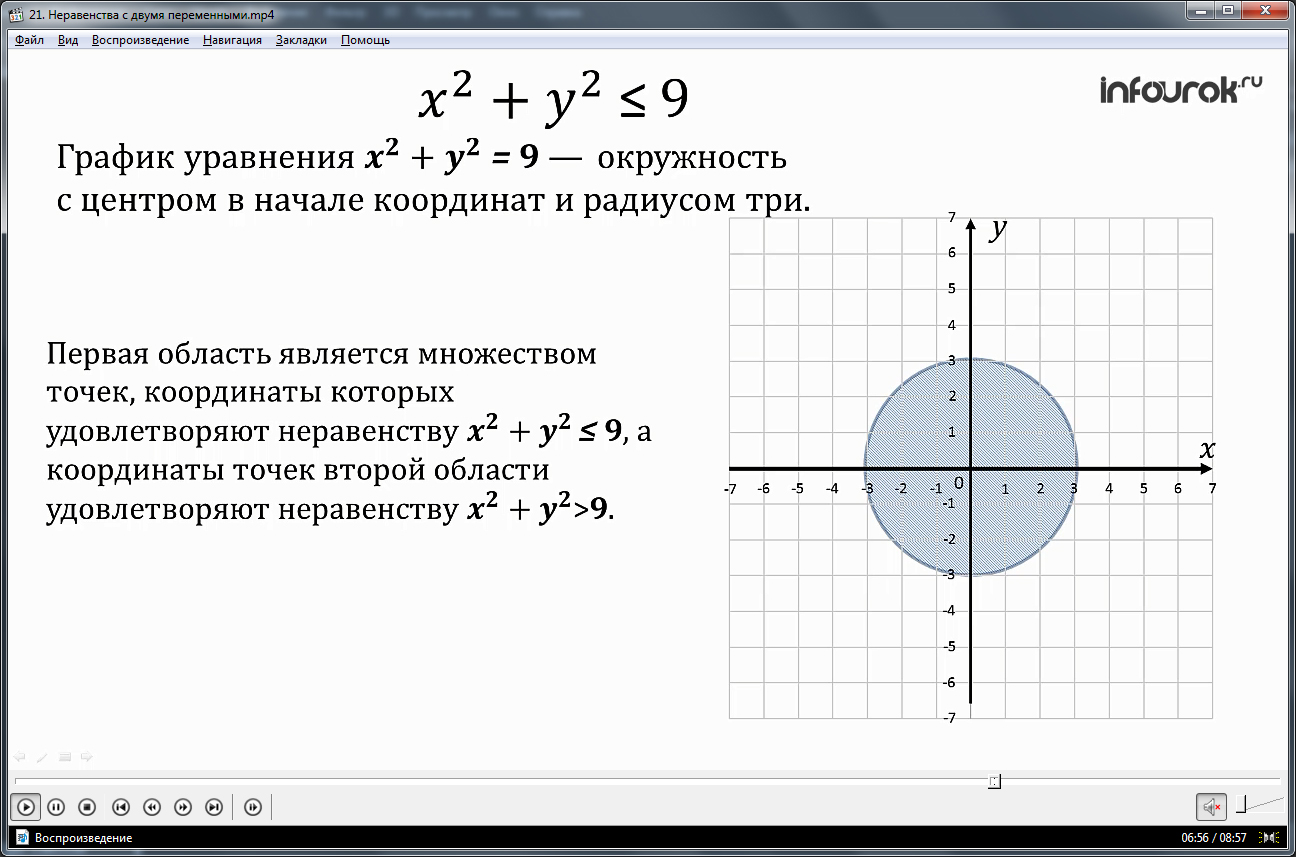
Следующим примером, демонстрирующим положение на плоскости точек, являющихся решением неравенства второй степени, является описание решения неравенства х2+у2<=9. На координатной плоскости строится окружность радиусом 3 с центром в начале координат. Отмечается, что решениями уравнения будут точки, сумма квадратов координат которых не превышает квадрата радиуса. Также отмечается, что окружность х2+у2=9 разбивает плоскость на области внутри окружности и вне круга. Очевидно, что множество точек внутренней части круга удовлетворяют неравенству х2+у2<9, а внешняя часть – неравенству х2+у2>9. Соответственно, решением исходного неравенства будет множество точек окружности и области внутри ее.
Далее рассматривается решение уравнения ху>8. На координатной плоскости рядом с заданием строится гипербола, удовлетворяющая уравнению ху=8. Отмечается точка М(х0;у0), принадлежащая гиперболе и К(х0;у) выше ее параллельно оси у. Очевидно, что координаты точки К соответствуют неравенству ху>8, так как произведение координат данной точки превосходит 8. Указывается, что таким же способом доказывается соответствие точек, принадлежащих области В, неравенству ху<8. Следовательно, решением неравенства ху>8 будет множество точек, лежащих в областях А и С.
Видеоурок «Неравенства с двумя переменными» может послужить наглядным пособием учителю на уроке. Также материал поможет ученику, самостоятельно осваивающему материал. Полезно использование видеоурока при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10325 |
| Номер материала | 665 |