
Урок «Неравенства с параметрами»

Краткое описание документа:
На этом уроке мы изучим алгоритм решения неравенств с параметрами и научимся применять его при решении такого типа заданий.
Определение первое.
Решить неравенство с параметром — значит для каждого значения параметра найти множество всех решений данного неравенства или доказать, что решений нет.
Рассмотрим линейные неравенства.
Определение второе.
Неравенства вида а икс плюс бэ больше нуля, больше либо равно нулю, меньше нуля, меньше либо равно нулю, где a и бэ — действительные числа, икс — переменная, называются неравенствами первой степени (линейными неравенствами).
Алгоритм решения линейного неравенства с параметром, например, неравенстваа икс плюс бэ больше нуля, где a и бэ — действительные числа, икс — переменная. Рассмотрим следующие случаи:
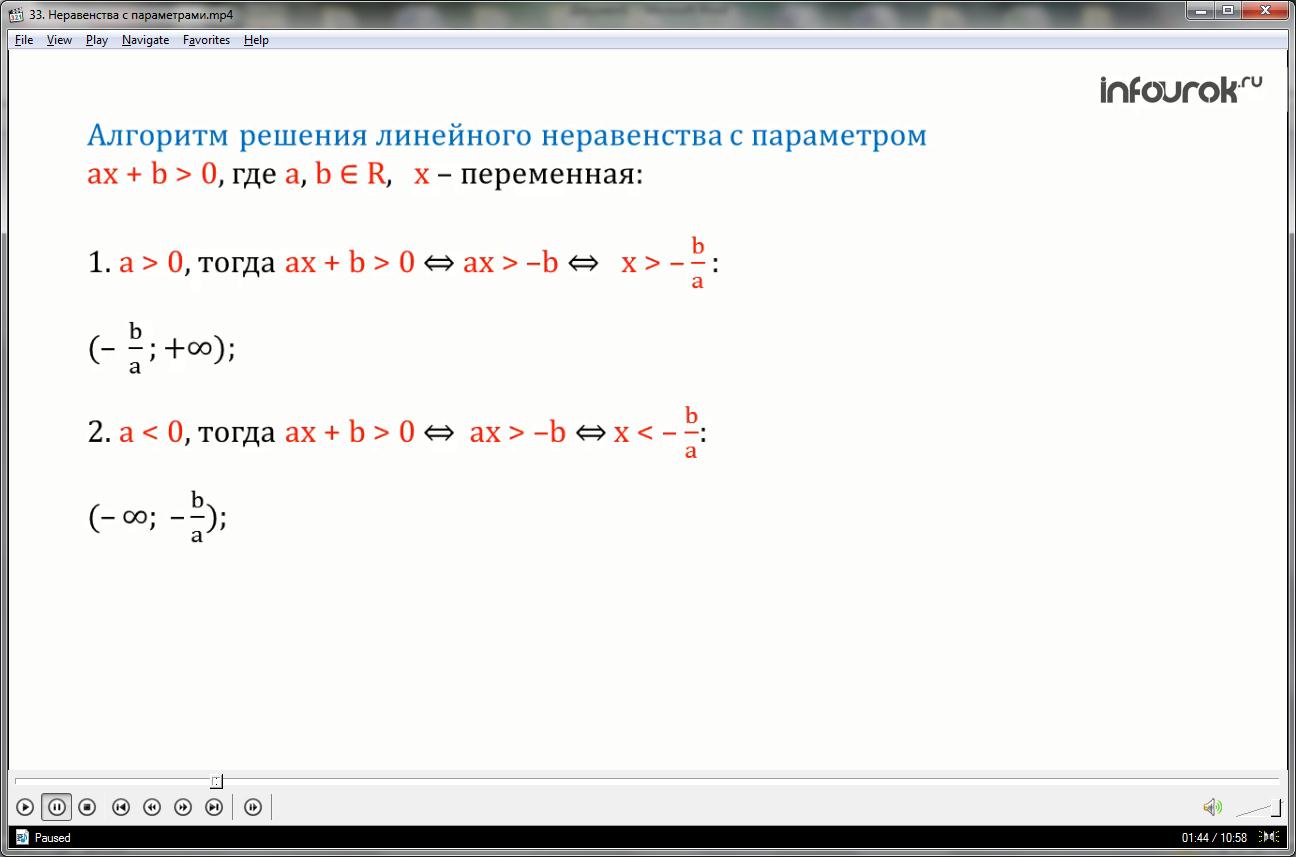
Первый случай: a больше нуля, тогда икс больше минус бэ деленное на а.
Следовательно, множество решений неравенства есть открытый числовой луч от минус бэ деленное на а до плюс бесконечности.
Второй случай: a меньше нуля, тогда икс меньше минус бэ деленное на а
и, следовательно, множество решений неравенства есть открытый числовой луч от минус бесконечности до минус бэ деленное на а.
Третий случай: a равно нулю, тогда неравенство примет вид: ноль умноженное на икс плюс бэ больше нуля и для бэ большенуля любое действительное число есть решение неравенства, а при бэ меньшем либо равным нулю неравенство не имеет решений.
Остальные неравенства решаются аналогично.
Рассмотрим примеры.
Задание 1
Решить неравенство а иксменьше либо равно единице.
Решение
В зависимости от знака a рассмотрим три случая.
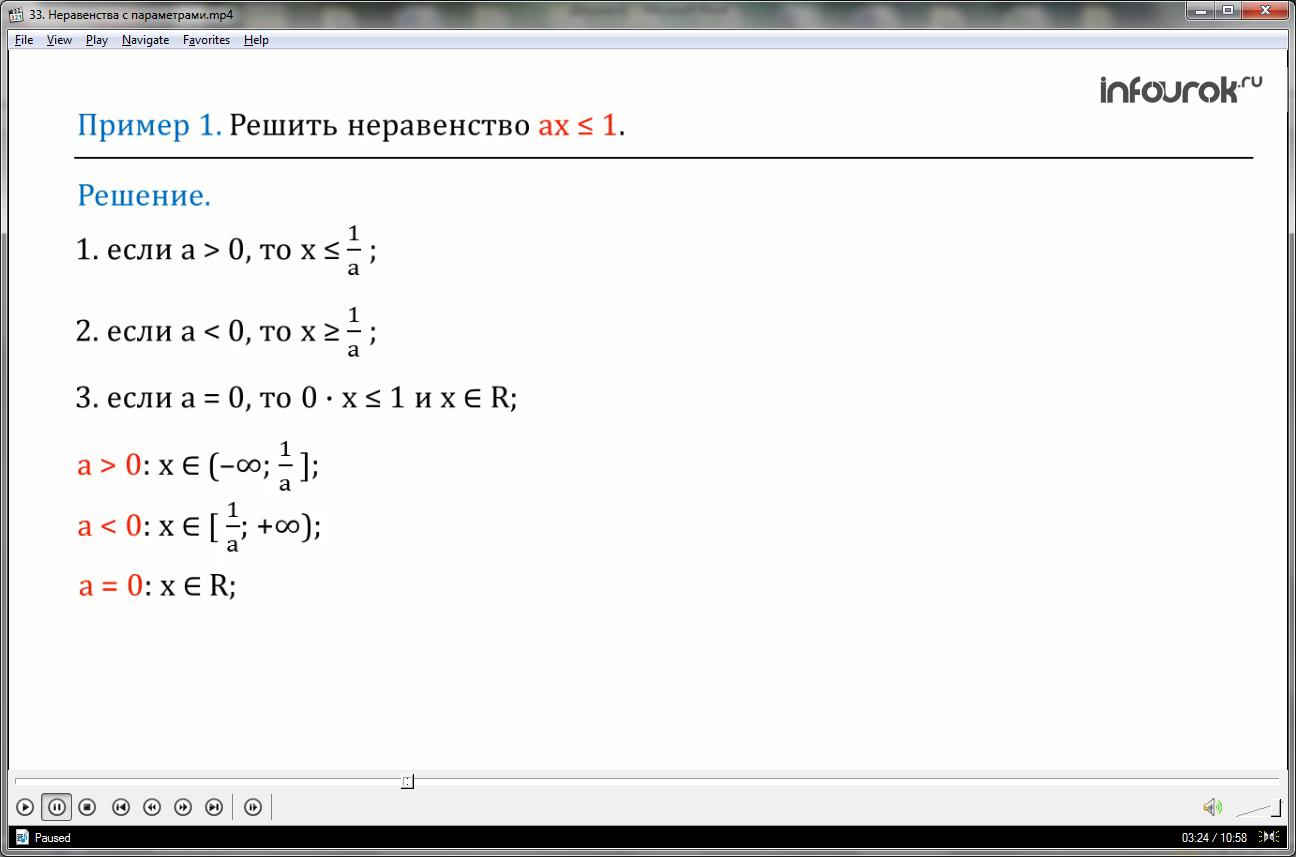
Первый случай: если a больше нуля, то икс меньше либо равно один деленное на а;
Второй случай: если a меньше нуля, то икс больше либо равно один деленное на а;
Третий случай: если a равно нулю, то неравенство примет вид: ноль умноженное на икс меньше, либо равно единице и, следовательно, любое действительное число является решением исходного неравенства.
Таким образом, если а больше нуля, то икс принадлежит лучу от минус бесконечности до единицы, деленной на а.
Если a меньше нуля, то икс принадлежит лучу от единицы, деленной на а, до плюс бесконечности, и если a равно нулю,
то x принадлежит множеству действительных чисел.
Ответ: если а больше нуля, то икс принадлежит лучу от минус бесконечности до единицы, деленной на а;
если a меньше нуля, то икс принадлежит лучу от единицы, деленной на а, до плюс бесконечности, и если a равно нулю,
то x икс принадлежит множеству действительных чисел.
Задание 2
Решить неравенство модуль икс минус два больше минус квадрата разности а и единицы.
Решение
Заметим, что модуль икс минус два больше либо равно нулю для любого действительного икс и минус квадрат разности а и единицы меньше либо равно нулю для любого значения параметра a. Следовательно, если a равно единице, то любое икс — действительное число, отличное от двух, является решением неравенства, а если a не равно одному, то любое действительное число является решением неравенства.
Ответ: если a равно одному, то икс принадлежит объединению двух открытых числовых лучей от минус бесконечности до двух и от двух до плюс бесконечности,
а если a принадлежит объединению двух открытых числовых лучей от минус бесконечности до единицы и от одного до плюс бесконечности, то икс принадлежит множеству действительных чисел.
Задание 3
Решить неравенство три умноженное на разность четырех а и икса меньше двух а икс плюс три.
Решение
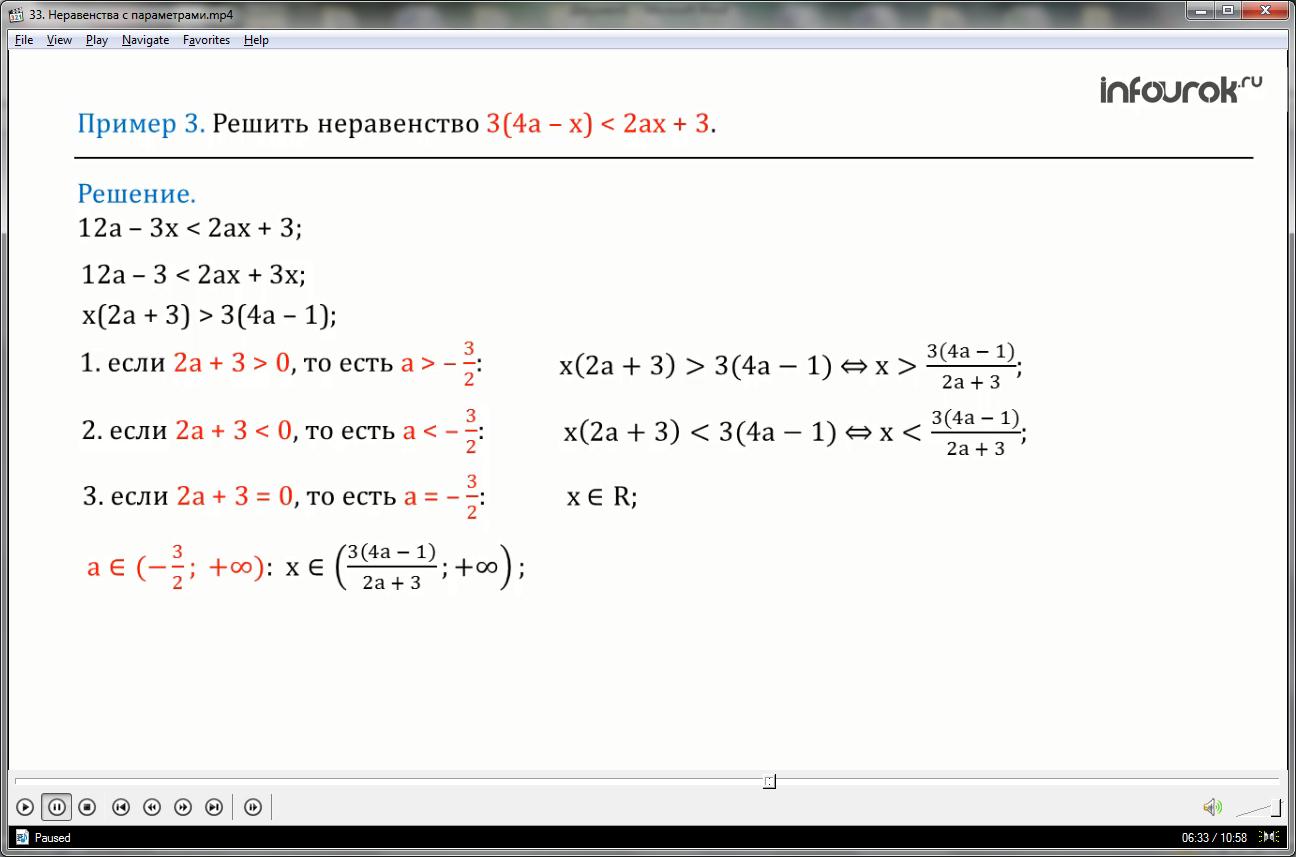
После элементарных преобразований данного неравенства, получим неравенство: икс умноженное на сумму двух а и трех больше три умноженное на разность четырех а и одного.
Далее рассмотрим три случая:
Первый случай: если два а плюс три больше нуля, то есть a больше минус трех вторых, то икс больше дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель — два а плюс три.
Второй случай: если два а плюс три меньше нуля, то есть a меньше минус трех вторых, то икс меньше дроби, числитель которой — три умноженное на разность четырех а и одного, а знаменатель два а плюс три.
Третий случай: если два а плюс три равно нулю, то есть a равно минус три вторых,
любое действительное число является решением исходного неравенства.
Следовательно, если а принадлежит окрытому числовому лучу от минус трех вторых до плюс бесконечности, то икс
принадлежит открытому числовому лучу от дроби, числитель которой — три умноженное на разность четырех а и одного, а знаменатель — два а плюс три, до плюс бесконечности.
Если а принадлежит открытому числовому лучу от минус бесконечности до минус трех вторых, то икс принадлежит открытому числовому лучу от минус бесконечности до дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель — два а плюс три;
если a равно минус трем вторых, то икс принадлежит множеству действительных чисел.
Ответ: если а принадлежит окрытому числовому лучу от минус трех вторых до плюс бесконечности, то икс
принадлежит открытому числовому лучу от дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель — два а плюс три до плюс бесконечности;
если а принадлежит открытому числовому лучу от минус бесконечности до минус трех вторых, то икс принадлежит открытому числовому лучу от минус бесконечности до дроби, числитель которой — три умноженное на разность четырех а и единицы, а знаменатель два а плюс три;
если a равно минус трем вторых, то икс принадлежит множеству действительных чисел.
Задание 4
Для всех допустимых значений параметра а решить неравенство квадратный корень из икс минус а плюс квадратный корень из двух а минус икс плюс квадратный корень из а минус один плюс квадратный корень из трех минус а больше нуля.
Решение
Найдем область определения параметра а. Она определяется системой неравенств, решив которую находим, что а принадлежит отрезку от одного до трех.
Данное неравенство равносильно системе неравенств, решая которую находим, что икс принадлежит отрезку от а до двух а.
Если а принадлежит отрезку от единицы до трех, то решением исходного неравенства является отрезок от а до двух а.
Ответ: если а принадлежит отрезку от одного до трех, тоикс принадлежит отрезку от а до двух а.
Задание 5
Найти все а, при которых неравенство
квадратный корень из икс в квадрате минус икс минус два плюс квадратный корень из дроби, числитель которой — два минус икс, а знаменатель — икс плюс четыре больше либо равно а икс плюс два минус квадратный корень из дроби, числитель которой — икс плюс один, а знаменатель — пять минус икс не имеет решения.
Решение
Первое. Вычислим область определения данного неравенства. Она определяется системой неравенств, решением которой являются два числа: икс равен минус единице и икс равен двум.
Второе. Найдем все значения а, при которых данное неравенство имеет решения. Для этого найдем все а, при которых икс равен минус единице и икс равен двум — это решение данного неравенства. Рассмотрим и решим совокупность двух систем. Решением является объединение двух числовых лучей от минус бесконечности до минус одной второй, и от единицы до плюс бесконечности.
Значит, данное неравенство имеет решение, если а принадлежит объединению двух числовых лучей от минус
бесконечности до минус одной второй, и от единицы до плюс бесконечности.
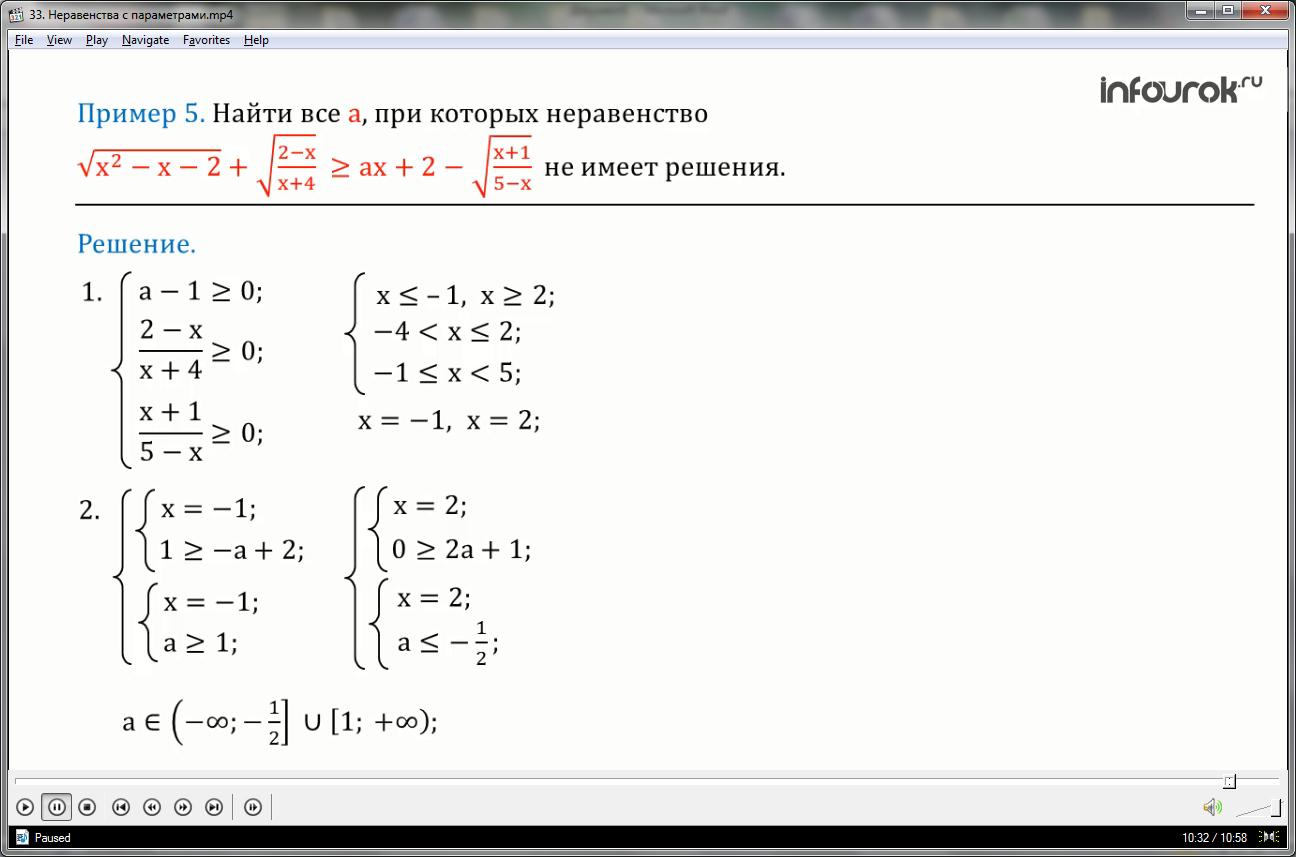
Третье. Следовательно, данное неравенство не имеет решения, если а принадлежит интервалу от минус одной второй до единицы.
Ответ: неравенство не имеет решения, если а принадлежит интервалу от минус одной второй до единицы.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10167 |
| Номер материала | 1082 |