
Урок "Область определения и область значений функции"

Краткое описание документа:
Урок по теме «Область определения и область значений функции» проводится в 10 классе в курсе алгебры и начал анализа. На объяснение материала по данной теме автор отводит 8:47 минут. этого времени достаточно для того, чтобы обучающиеся прослушали необходимую информацию, зафиксировали ее в своих тетрадях и поняли содержание материала. Примерно столько же времени затрачивает учитель на уроке при объяснении нового материала.
Автор позаботился об учителях, нагрузка которых итак достаточно велика, поэтому разработал данный видеоурок с учетом всех требований. То есть, урок соответствует возрасту обучающихся, их уровню образования и особенностей восприятия материала. Учителю останется лишь подобрать материал для закрепления новой информации, полученной из данного урока.
Урок начинается с информации о том, что функция задается вместе с областью определения. Далее автор определяет переменные xи y? как аргумент и значение функции соответственно. После этого вводятся определения понятий область определения функции и область значений функции.
Затем рассматривается пример, где функция задана графически, и необходимо определить ее область определения. Решение данного примера подробно расписывается на экране. Автор поясняет каждый момент, где обучающиеся могут допустить ошибки. Все объяснение сопровождается наглядной иллюстрацией на рисунке.
Далее автор переходит к пункту «Область определения рациональной функции». Для обучающихся говорится о том, что в область определения рациональных функций не входят те значения аргумента, которые обращают знаменатель в нуль. Это поясняется на случае общего написания рациональной функции.
Затем на этот случай рассматривается пример. Здесь необходимо найти область определения рациональной функции. Решение пример основано на той информации, которую только что автор поведал обучающимся. То есть, он находит все те значения, которые обращают знаменатель в нуль и исключает их из множества действительных чисел, получая, таким образом, область определения функции.
после этого предлагается рассмотреть еще один пример, где требуется найти область определения рациональной функции. Но здесь наблюдается следующая особенность: знаменатель дроби никогда не обращается в нуль. Поясняя это, автор делает вывод, что областью определения данной функции является множество действительных чисел. После этого примера предлагается запомнить закономерность, которая только что была использована в примере.
Далее автор переходит к пункту «Область определения иррациональной функции». Здесь важно запомнить то, что подкоренное выражение никогда не может быть отрицательным. Это подкрепляется математической интерпретацией на математической языке. Здесь же поясняется, что если иррациональное выражение в записи функции находится в знаменателе, то подкоренное выражение будет не просто неотрицательным, а строго положительным.
К этому материалу прилагается пример, где требуется найти область определения иррациональной функции. Решая неравенство: подкоренное выражение неотрицательно, автор получает значения аргумент, которые образуют область определения заданной функции.
Затем рассматривается область определения функции с натуральным логарифмом. Сначала дается теоретический экскурс по данному материалу, а затем приводится пример с подробным описанием каждого шага решения.
После всего теоретического материала автор предлагает рассмотреть три примера, где требуется найти область определения и область значений функции, заданной графически. Это можно использовать как небольшой элемент закрепления выданного только что материала.
Урок будет полезен не только учителям, но и обучающимся, которые занимаются самообразованием или пропустили урок по данной теме по определенным причинам. Из этого урока обучающиеся смогут почерпнуть не только теоретический материал, но и подкрепить полученные знания практическими упражнениями.
ТЕКСТОВАЯ РАСШИФРОВКА:
Область определения и область значений функции.
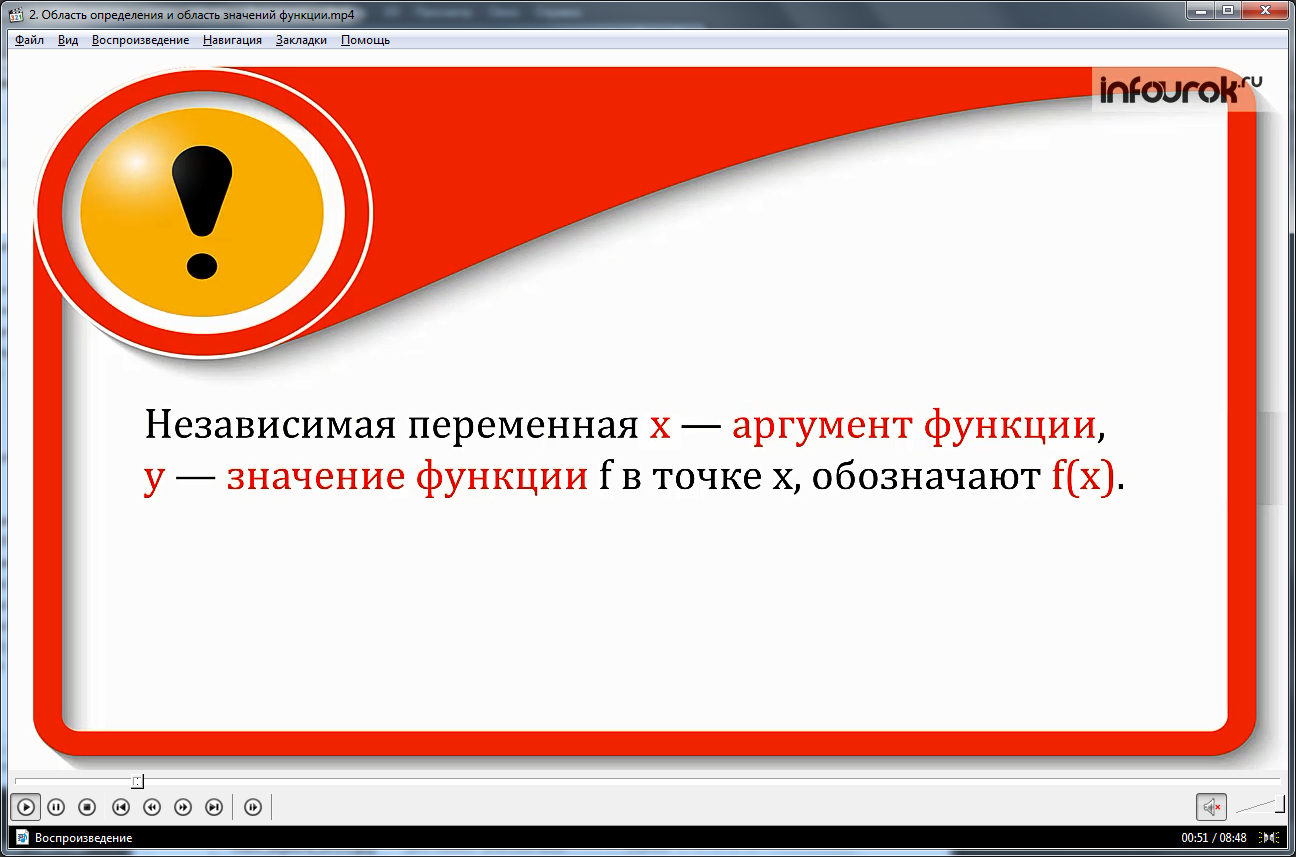
Из определения функции следует, что функция игрек равен эф от икс задается вместе с ее областью определения икс большое.
Для изучения этой темы нам необходимо вспомнить: как называется переменная икс? число у?
Независимую переменную икс называют аргументом функции, а число игрек, соответствующее числу икс, называют значением функции эф в точке икс и обозначают эф от икс
Какое множество называется областью определения функции?
Если нам дана функция у=f(х),то ее область определения – это множество значений «икс», для которых существуют значения «игрек»и обозначают дэ большое от эф.
Область значений функции – множество, состоящее из всех чисел эф от х, таких, что икс принадлежит икс большому и обозначают е большое от эф.
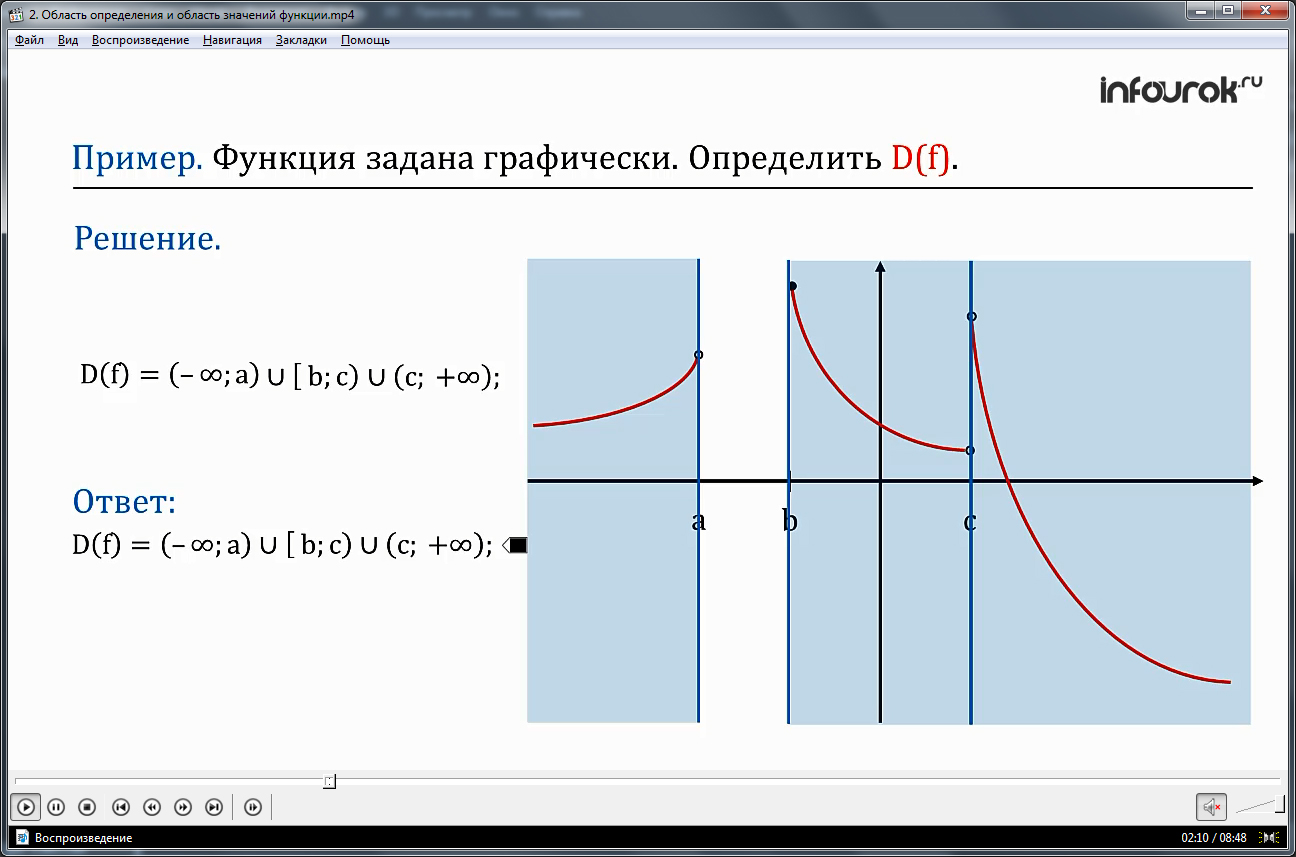
Рассмотрим пример. Функция задана графически. Определить дэ большое от эф.
Область определения данной функции представляет собой объединение промежутков:
интервал от минус бесконечности до а, луч от вэ до цэ и интервал от цэ до плюс бесконечности. Действительно так, если взять любое значение «икс» из интервала от минус бесконечности до а, или из полуинтервала от вэ до цэ, или из интервала от цэ до плюс бесконечности, то для каждого такого «икс» будет существовать значение «игрек».
Как найти область определения функции?
Рассмотрим примеры.
Первое.
Область определения рациональной функции, т.е. аргумент у которой есть в содержится в знаменателе.
Запомните:
значения аргумента, которые обращают знаменатель в ноль – не входят в область определения данной функции.
Предположим, дана функция, содержащая некоторую дробь единица, деленная на альфа от ихс. Как вы знаете, на ноль делить нельзя: поэтому альфа от икс не равно нулю
Найти область определения функции
эф от икс равен дроби, числитель которой икс плюс два, а знаменатель – икс квадрат минус три. Данная функция задана аналитически.
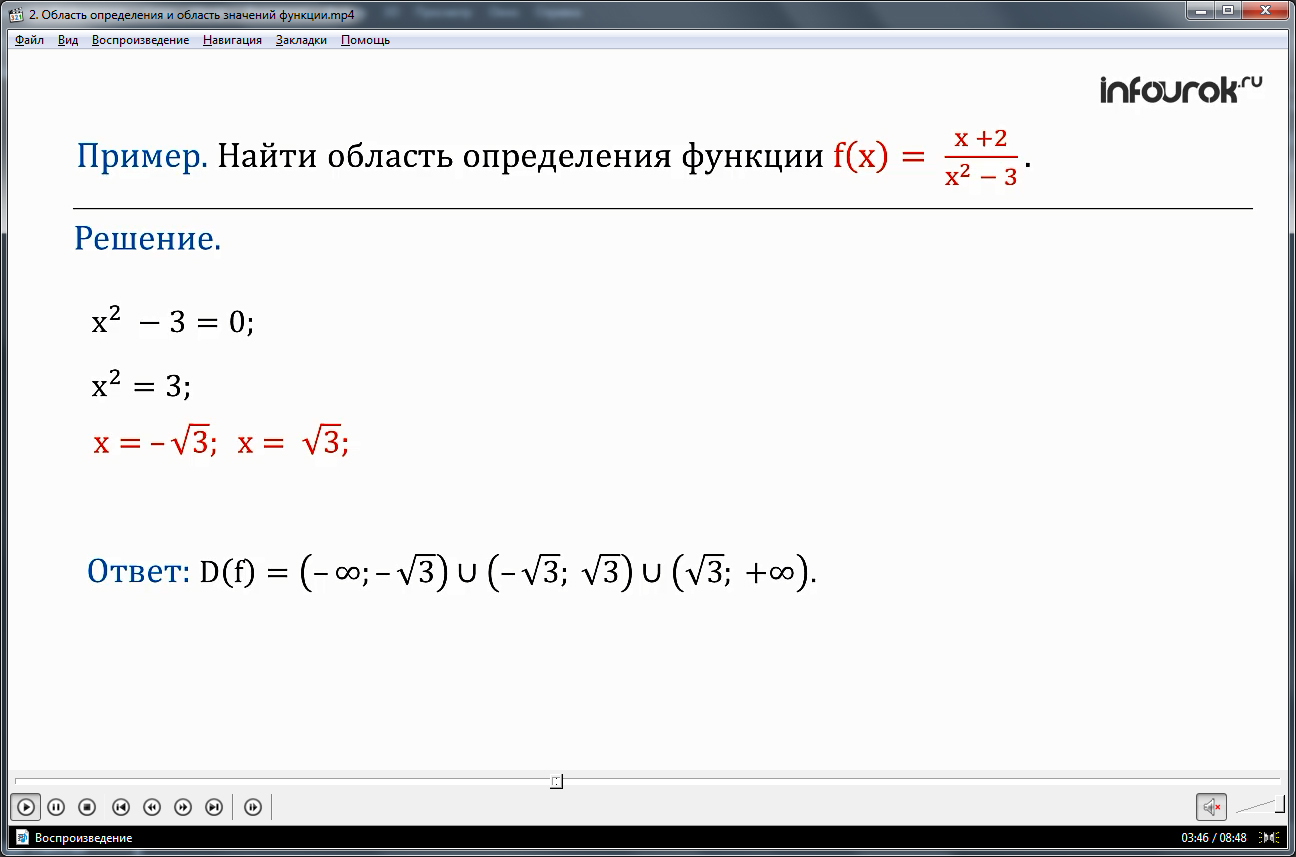
Решение: обращаем внимание на знаменатель, он должен быть не нулевым. Приравняем его к нулю и найдем значение аргумента которые обращают знаменатель функции в ноль:
икс квадрат минус триравно нулю.
икс квадрат равно трем.
Полученное уравнение имеет два корня:
минус квадратный корень из трех, квадратный корень из трех.
Данные значения не входят в область определения функции, так как при этих значениях знаменатель дроби обращается в ноль.
Ответ: дэ большое от эф равен объединению промежутков:интервал от минус бесконечности до квадратного корня из трех,интервал от минус квадратного корня из трех до квадратного кореня из трех.
и интервал от квадратного кореня из трех
до плюс бесконечности.
Рассмотрим еще пример.
Найти область определения функции
эф от икс равен дроби, числитель которой единица, а знаменатель – икс квадрат плюс один.
Решение
Рассмотрим выражение стоящее в знаменателе: к квадрату числа икс прибавляют единицу он всегда положительно т.е. какое бы значение «икс» мы не взяли, знаменатель не обратится в ноль, более того, будет всегда положителен, значит область определения функции, дэ большое от эф равено множеству всех действительных чисел.
определена на всей числовой оси.
Запомните!
при любом значении «икс» и положительной константе ка:
икс квадрат плюс ка больше нуля.
Второе.
Область определения иррациональной функции ( содержащий радикал или корень).
Запомни.
подкоренное выражение неотрицательно
Функция вида игрек равен квадратный корень из альфа от икс определена только при тех значениях икс из области определения дэ от альфа, когда альфа от икс не отрицательно, т.е. больше или равна нулю. Если функция содержащая радикал в знаменателе дроби, то альфа от х строго больше нуля.
Найти область определения функции
эф от икс равен квадратный корень из трех минус два икс.
Решение: подкоренное выражение должно быть неотрицательным:
три минус два икс больше или равно нулю
минус два икс больше или равно минус трем
два икс меньше или равно трем
икс меньше или равнотрем вторым
Ответ: дэ большое от эф равен полуинтервалу от минус бесконечности до трех вторых.
Третье.
Область определения функций с натуральным логарифмом.
Запомни.
Пусть функция содержит натуральный логарифм альфа от икс., то в её область определения входят только те значения икс, удовлетворяющие неравенству альфа от икс строго больше нуля.
Если логарифм находится в знаменателе: то дополнительно накладывается условие альфа от икс не равно единице, (так как натуральный логарифм единицы равен нулю).
Найти область определения функции
эф от икс равен дроби числитель равен единице, а знаменатель – натуральный логарифм из выражения икс плюс три.

Решение: в соответствии с вышесказанным составим и решим систему:
икс плюс три больше нуля
и икс плюс три не равно единице
отсюда,
икс больше минус трех и икс не равно минус двум.
Изобразим множество решений системы на прямой и сделаем вывод.
Ответ: дэ большое от эф равно объединению промежутков: интервалам от минус трех до минус двух и от минус двух до плюс бесконечности.
Найтиобласть определения и область значений функции.
Дэ большое от эф равен отрезку от минус четырех до двух;
Е большое от эф равно отрезку от минус одного до двух;
Найтиобласть определения и область значений функции.
Дэ большое от эф равен интервалу от минус двух до пяти;
Е большое от эф равно отрезку от минус двух до трех;
Найтиобласть определения и область значений функции.
Дэ большое от эф равен отрезку от минус четырех до трех;
Е большое от эф равно отрезку от минус пяти до нуля;
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7595 |
| Номер материала | 825 |