
Урок «Обобщение понятия о показателе степени»

Краткое описание документа:
Вы уже знакомы со способами вычисления значения степени с целым показателем, применяя следующие свойства:
1. если n=1, то а1=а
2. если n =0, при этом а≠0, то а0=1
3. если n N, n≥2, то аn=а*а*а*а…( n множителей).
(Если а принадлежит множеству натуральных чисел и а больше или равно двум, то можно записать: а в степени эн равно а*а*а*а…( n множителей).
4. если n=1, 2, 3, …и а≠0, то а- n=
(Если эн равно 1, 2, 3, и так далее и а не равно нулю, то а в степени минус эн можно представить как один деленное на а в степени эн).
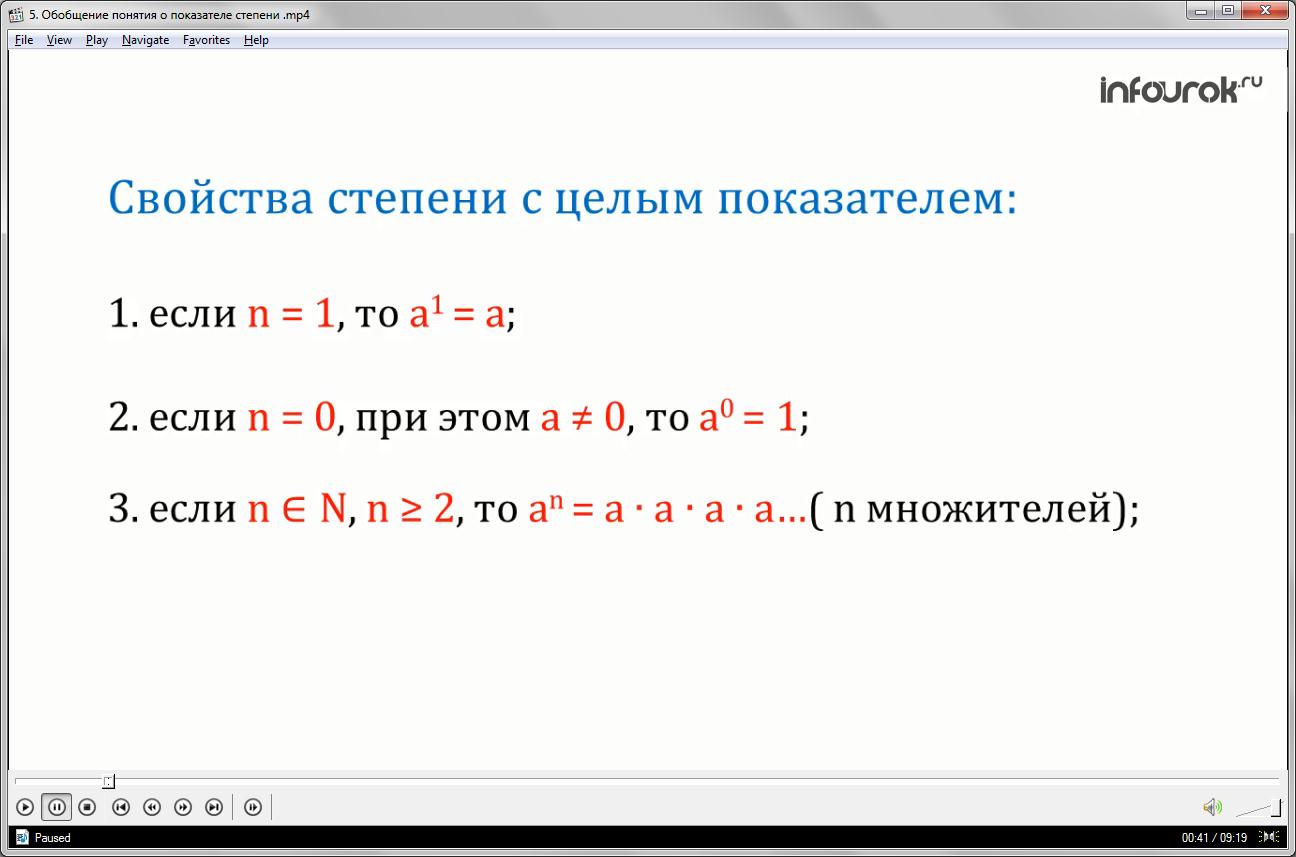
Свойства степени с целым показателем:
1. если n=1, то а1=а
2.если n =0, при этом а≠0, то а0=1
3.если n N, n≥2, то аn=а*а*а*а…( n множителей).
4.если n=1, 2, 3, …и а≠0, то а- n=
Например:
1. 51=5 (пять в первой степени равно пяти)
2. С0 =1, кроме 00 – не определено
(любая переменная или постоянная в нулевой степени всегда даёт единицу, кроме нуль в нулевой не определено),
3. 138=13*13*13…*13 (8 множителей)
4. 4*16-1=4* = =0,25 (4 умножить на 16 в минус первой степени равно 4 умножить на одну шестнадцатую, сокращаем 4 и 16 на 4, получим одну четвёртую или ноль целых 25 сотых).
1. 51=5
2. С0=1, кроме 00–не определено
3. 138=13*13*13…*13(8 множителей)
4. 4*16-1=4* = =0,25
Но в математике показателем степени может быть не только целое число, но и положительное рациональное (дробное) число.
К примеру: 40,4 (4 в степени ноль целых четыре десятых)
или (одна целая три десятых в степени три седьмых). Пример добей с рациональным положительным показателем:
40,4 ;
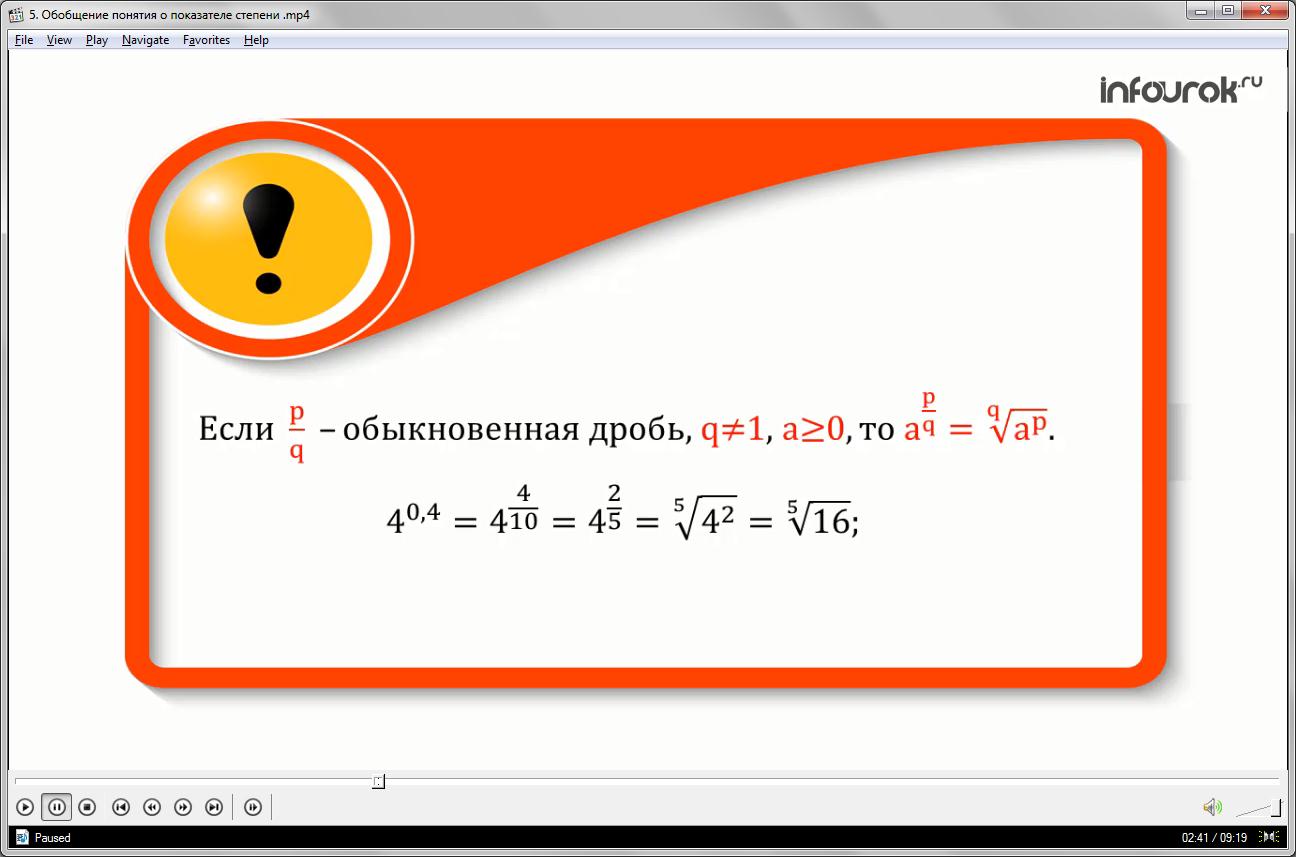
Итак, если - обыкновенная дробь, причём ку не равно единице и а больше или равно нулю, то под выражением а в степени пэ делённое на ку понимают корень степени ку из а в степени пэ.
Таким образом, 4 в степени ноль целых четыре десятых можно записать в виде: 4 в степени четыре десятых, сократим показатель степени на 2, получим 4 в степени две пятых, по определению степени с рациональным показателем, получим корень пятой степени из четырёх в квадрате или корень пятой степени из шестнадцати:
40,4= = = =
Аналогично можно записать и число одна целая три десятых в степени три седьмых:
Получим корень седьмой степени из числа одна целая три десятых в кубе.
Помимо определения степени с положительным рациональным показателем, существует так же определение степени с отрицательным рациональным показателем.
Итак, если - обыкновенная дробь, причём ку не равно единице и а строго больше ноля, то под выражением а в степени минус пэ делённое на ку понимают один делённое на а в степени пэ делённое на ку или один делённое на корень степени ку из а в степени пэ.
Например, три в степени минус две третьих по определению запишется как — один делённое на три в степени две третьих или один делённое на корень кубический из трёх в квадрате, три в квадрате – это 9 таким образом, мы получили, что три в степени минус две третьих — это один делённое на корень кубический из девяти.
В случае степени с любым рациональным показателем выполнимы все свойства степени с целым показателем (будем считать, что а>0, b>0, m и n-любые рациональные числа):
1) am*an=am+n
2) am:an=am-n
3) (am)n=amn
4) (ab)m=am*bm
5) =
Свойства степени с любым рациональным показателем
(а>0, b>0, m и n- любые рациональные числа):
1). am*an=am+n
2). am:an=am-n
3). (am)n=amn
4). (ab)m=am*bm
5). =
Рассмотрим применение изученных свойств на конкретных примерах:
Пример 1.
Вычислить:
а) 64 в степени одна шестая;
б) 27 в степени две третьих;
в) 0 в степени пятьдесят одна четвёртая;
г) минус восемь в степени одна третья.
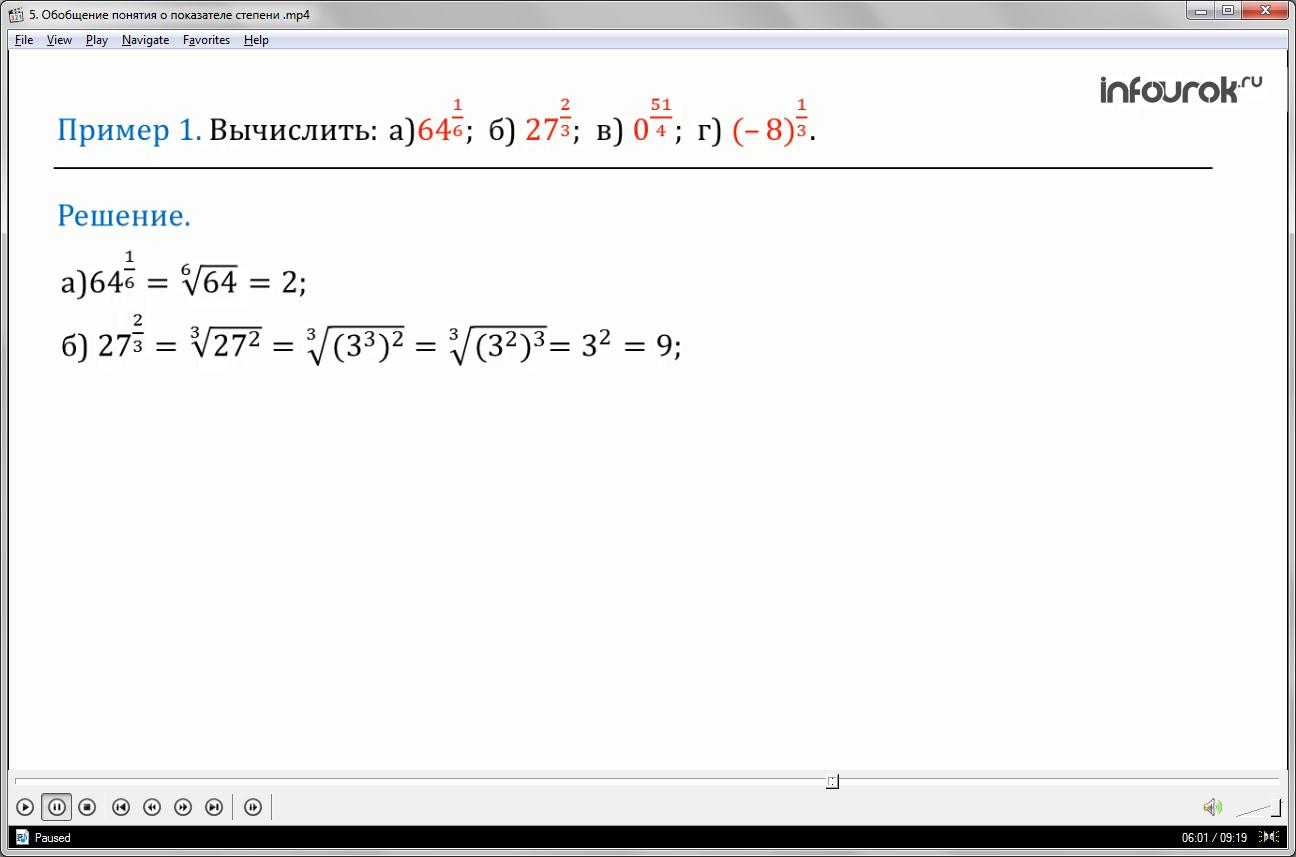
Решение:
а) Воспользуемся определением степени с рациональным показателем:
64 в степени одна шестая равно корень шестой степени из шестидесяти четырёх, а это 2.
б) Аналогично можно записать, что 27 в степени две третьих — это кубический корень из двадцати семи в квадрате, 27 можно представить в виде три в кубе, получим — корень кубический из трёх в кубе и в квадрате, по свойству три меняем местами множители в степени получаем корень кубический из трех в квадрате и кубе. Таким образом, извлекая кубический корень из трёх в квадрате и в кубе и возводя три в квадрат, получим 9.
в) Очевидно, что число 0 в любой степени всегда даёт ноль, итак, 0 в степени пятьдесят одна четвёртая — это ноль.
г) Определения степени с дробным показателем для случая отрицательного основания не существует, таким образом, запись минус восемь в степени одна третья не имеет смысла. Пример 1.
Пример 2.
Упростить выражение:
Решение:
1) Упростим выражение икс в степени одна третья плюс игрек в степени одна третья всё это в квадрате, применяя формулу квадрата суммы , получим икс в степени одна третья и в квадрате плюс удвоенное произведение икса в степени одна третья и игрека в степени одна третья плюс игрек в степени одна третья и в квадрате. По свойству возведения степени в степень (am)n=amn раскроем скобки, возводя последовательно икс в степени одна третья в квадрат и игрек в степени одна третья в квадрат.
Получим, икс в степени две третьих плюс удвоенное произведение икса в степени одна третья и игрека в степени одна третья плюс игрек в степени две третьих.
2) Упростим выражение два умноженное на корень кубический из икса и игрека. Последовательно применяя определение степени с рациональным показателем = , а так же свойство возведения произведения в степень (ab)m=am*bm представим выражение в виде: два умноженное на икс в степени одна третья и игрек в степени одна третья.
3) Преобразуем выражение один деленное на корень кубический из игрек в минус второй степени, применяя определение степени с целым отрицательным показателем и степени с рациональным показателем = , а также свойство возведения степени в степень (am)n=amn получим игрек в степени две третьих.
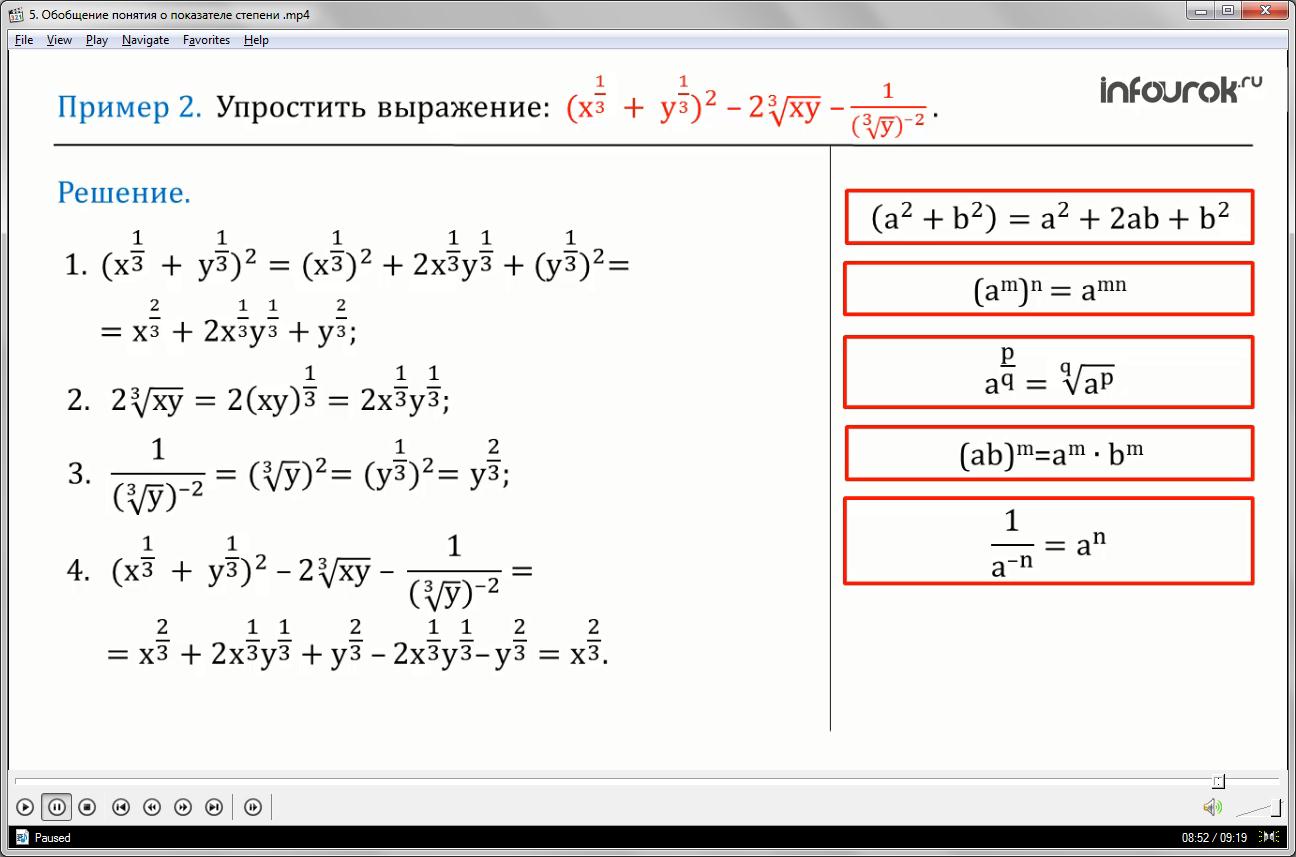
4) Подставим полученные после упрощения выражения в искомое, получим
икс в степени две третьих плюс удвоенное произведение икса в степени одна третья и игрека в степени одна третья плюс игрек в степени две третьих, минус два умноженное на икс в степени одна третья и игрек в степени одна третья и минус игрек в степени две третьих.
Приведём подобные слагаемые, в результате получим ответ: икс в степени две третьих. Пример 2.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6332 |
| Номер материала | 1054 |