
Урок "Однородные тригонометрические уравнения"

Краткое описание документа:
С помощью этого видеоурока учащиеся смогут изучить тему однородных тригонометрических уравнений.
Дадим определения:
1) однородное тригонометрическое уравнение первой степени выглядит как a sin x + b cos x = 0;
2) однородное тригонометрическое уравнение второй степени выглядит как a sin2 x + b sin x cos x + c cos2 x = 0.
Рассмотрим уравнение a sin x + b cos x = 0. Если а будет равно нулю, то уравнение будет выглядеть как b cos x = 0; если b равно нулю, то уравнение будет выглядеть как a sin x = 0. Это уравнения, которые мы называли простейшими и решали ранее в предыдущих темах.
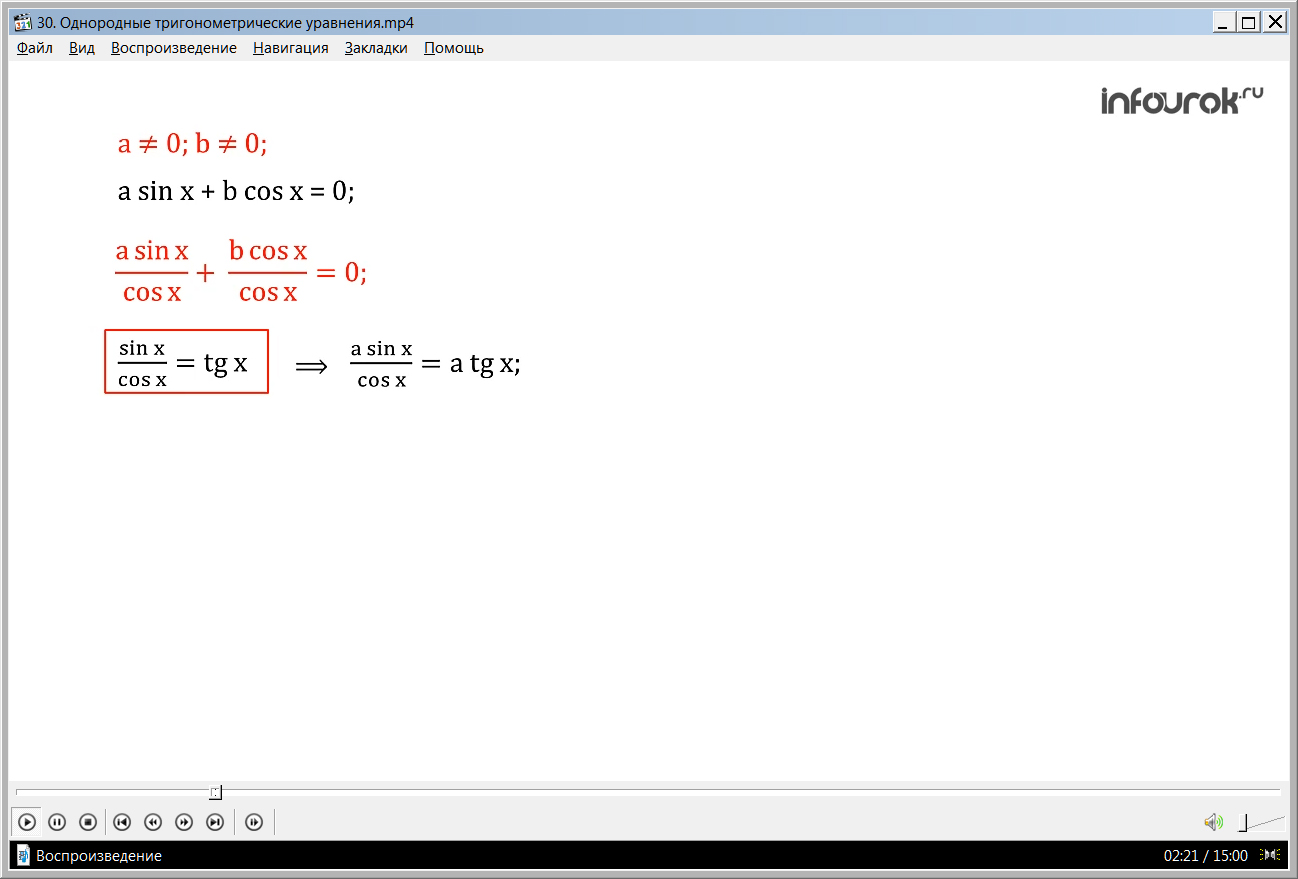
Сейчас рассмотрим вариант, когда a и b не равны нулю. С помощью деления частей уравнения на косинус x и осуществим преобразование. Получим a tg x + b = 0, тогда tg x будет равен – b/а.
Из вышеизложенного следует вывод, что уравнение a sin mx + b cos mx = 0 является однородным тригонометрическим уравнением I степени. Чтобы решить уравнение, его части делят на cos mx.
Разберем пример 1. Решить 7 sin (x/2) – 5 cos (x/2) = 0. Сначала части уравнения делим на косинус(x/2). Зная, что синус, деленный на косинус, это тангенс, получим 7 tg (x/2) – 5 = 0. Преобразовывая выражение, найдем, что значение тангенса (x/2)равно 5/7. Решение данного уравнения имеет вид х = arctg a + πn, в нашем случае х = 2 arctg (5/7) + 2πn.
Рассмотрим уравнение a sin2 x + b sin x cos x + c cos2 x = 0:
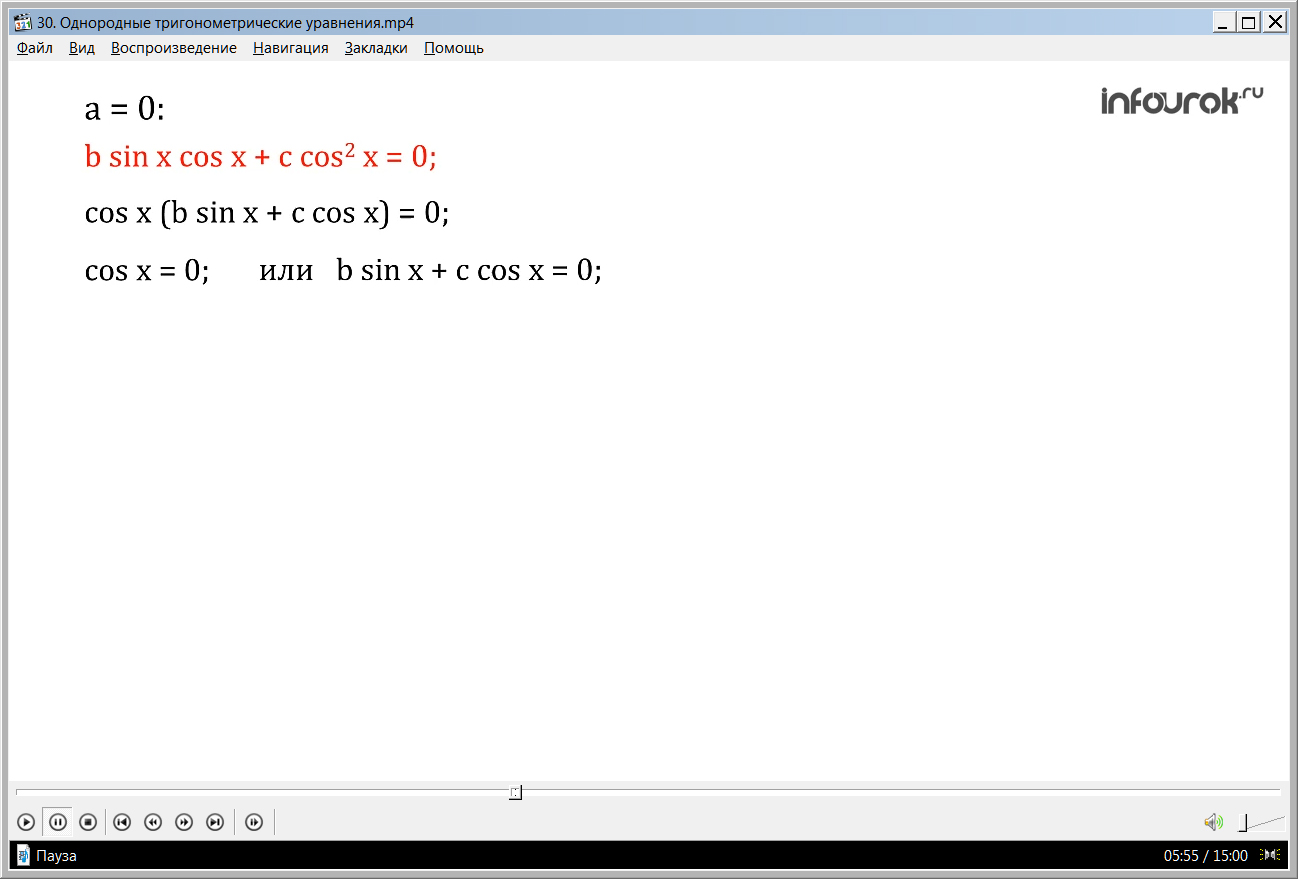
1) при а равном нулю уравнение будет выглядеть как b sin x cos x + c cos2 x = 0. Преобразуя, получим выражение cos x (b sin x + c cos x) = 0 и перейдем к решению двух уравнений. После деления частей уравнения на косинус x, получим b tg x + c = 0, а значит tg x = – c/b. Зная, что х = arctg a + πn, то решением в данном случае будет х = arctg (– с/b) + πn.
2) если а не равно нулю, то, путем деления частей уравнения на косинус в квадрате, получим уравнение, содержащее тангенс, которое будет квадратным. Это уравнение можно решить путем ввода новой переменной.
3) при с равном нулю уравнение примет вид a sin2 x + b sin x cos x = 0. Это уравнение можно решить, если вынести синус x за скобку.
Далее автор акцентирует внимание на том, что при решении уравнения a sin2 x + b sin x cos x + c cos2 x = 0 можно использовать следующие шаги:
1. посмотреть, есть ли в уравнении a sin2 x;
2. если в уравнении член a sin2 x содержится, то решить уравнение можно путем деления обеих частей на косинус в квадрате и последующим введением новой переменной.
3. если в уравнении a sin2 x не содержится, то решить уравнение можно с помощью выноса за скобки cosx.
Рассмотрим пример 2. Вынесем за скобки косинус и получим два уравнения. Корень первого уравнения x = π/2 + πn. Для решения второго уравнения разделим части этого уравнения на косинус x, путем преобразований получим х = π/3 + πn. Ответ: x = π/2 + πn и х = π/3 + πn.
Решим пример 3, уравнение вида 3 sin2 2x – 2 sin 2x cos 2x + 3 cos2 2x = 2 и найдем его корни, которые принадлежат отрезку от – π до π. Т.к. это уравнение неоднородное, необходимо привести его к однородному виду. Используя формулу sin2 x + cos2 x = 1, получим уравнение sin22x – 2 sin 2x cos 2x + cos2 2x = 0. Разделив все части уравнения на cos2 x, получим tg2 2x + 2tg 2x + 1 = 0. Используя ввод новой переменной z = tg 2x, решим уравнение, корнем которого будет z = 1. Тогда tg 2x = 1, откуда следует, что x = π/8 + (πn)/2. Т.к. по условию задачи нужно найти корни, которые принадлежат отрезку от – π до π, решение будет иметь вид – π< x <π. Подставляя найденное значение x в данное выражение и преобразовывая его, получим – 2,25 < n < 1,75. Т.к. n - это целые числа, то решению уравнения удовлетворяют значения n: – 2; – 1; 0; 1. При этих значениях n получим корни решения исходного уравнения: x = (– 7π)/8, x = (– 3π)/8, x =π/8, x = 5π/8.
ТЕКСТОВАЯ РАСШИФРОВКА:
Однородные тригонометрические уравнения
Сегодня мы разберем, как решаются «Однородные тригонометрические уравнения». Это уравнения специального вида.
Познакомимся с определением.
Уравнение вида а sin x+bcosx = 0(а синус икс плюс бэ косинус икс равно нулю) называют однородным тригонометрическим уравнением первой степени;
уравнение вида а sin2 x+b sin x cosx +с cos2x= 0 (а синус квадрат икс плюс бэ синус икс косинус икс плюс сэ косинус квадрат икс равно нулю) называют однородным тригонометрическим уравнением второй степени.
Если а=0, то уравнение примет вид bcosx = 0.
Еслиb = 0, то получим а sin x= 0.
Данные уравнения являются элементарными тригонометрическими, и их решение мы рассматривали на прошлых наших темах
Рассмотрим тот случай, когда оба коэффициента не равны нулю. Разделим обе части уравнения а sinx+bcosx = 0 почленно на cosx.
Это мы можем сделать, так как косинус икс отличен от нуля. Ведь, если cosx = 0, то уравнение а sinx+bcosx = 0 примет вид а sinx = 0, а ≠ 0, следовательно sinx = 0. Что невозможно, ведь по основному тригонометрическому тождеству sin2 x+ cos2x=1.
Разделив обе части уравнения а sinx+bcosx = 0 почленно на cosx, получим: + =0
Осуществим преобразования:
1. Так как = tg x, то = а tg x
2 сокращаем на cosx, тогда
Таким образом получим следующее выражение а tg x + b =0.
Осуществим преобразование:
1.перенесем b в правую часть выражения с противоположным знаком
а tg x =- b
2. Избавимся от множителя а разделив обе части уравнения на а
tg x= - .
Вывод: Уравнение вида а sin mx+bcosmx = 0 (а синус эм икс плюс бэ косинус эм икс равно нулю) тоже называют однородным тригонометрическим уравнением первой степени. Чтобы решить его, делят обе части на cosmx.
ПРИМЕР 1. Решить уравнение 7 sin - 5 cos = 0 (семь синус икс на два минус пять косинус икс на два равно нулю)
Решение. Разделим обе части уравнения почленно на cos, получим
1. = 7 tg (так как соотношение синуса к косинусу – это тангенс, то семь синус икс на два деленное на косинус икс на два, равно 7 тангенс икс на два)
2. -5 = -5 (при сокращении cos )
3. =0
Таки образом получили уравнение
7tg - 5 = 0, Преобразуем выражение, перенесем минус пять в правую часть, изменив знак.
7 tg 5
tg = ,
Мы привели уравнение к виду tg t = a, где t=, a =. А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид
х = arctg a + πn, то решение нашего уравнения будет иметь вид:
= arctg + πn, найдем х
х=2 arctg + 2πn.
Ответ: х=2 arctg + 2πn.
Перейдем к однородному тригонометрическому уравнению второй степени
а sin2 x+b sin x cos x +сcos2 x= 0.
Рассмотрим несколько случаев.
I. Если а=0, то уравнение примет вид bsinxcosx +с cos2x= 0.
При решении это уравнения используем метод разложения на множители. Вынесем cosx за скобку и получим: cosx(bsinx +с cosx)= 0. Откуда cosx= 0 или
b sin x +сcos x= 0.А эти уравнения мы уже умеем решать.
Разделим обе части уравнения почленно на cosх, получим
1 (так как соотношение синуса к косинусу – это тангенс).
2.
Таким образом получаем уравнение: btg х+с=0
Мы привели уравнение к виду tg t = a, где t= х, a =. А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид
х = arctg a + πn, то решение нашего уравнения будет:
х = arctg + πn, .
II. Если а≠0, то обе части уравнения почленно разделим на cos2x.
(Рассуждая аналогично, как и в случае с однородным тригонометрическим уравнением первой степени, косинус икс не может обратится в ноль).
III. Если с=0, то уравнение примет вид а sin2x+bsinxcosx= 0. Это уравнение решается методом разложения на множители (вынесем sinxза скобку).
Значит, при решении уравнения а sin2x+bsinxcosx +с cos2x= 0 можно действовать по алгоритму:
ПРИМЕР 2. Решить уравнение sinxcosx - cos2x= 0 (синус икс, умноженный на косинус икс минус корень из трех, умноженный на косинус квадрат икс равно нулю).
Решение. Разложим на множители (вынесем за скобку cosx). Получим
cos x(sin x - cos x)= 0, т.е. cos x=0 илиsin x - cos x= 0.
Ответ: х =+ πn, х= + πn.
ПРИМЕР 3. Решить уравнение 3sin2 2x - 2 sin2xcos2 x +3cos2 2x= 2 (три синус квадрат двух икс минус удвоенное произведение синуса двух икс на косинус двух икс плюс три косинус квадрат двух икс) и найти его корни, принадлежащие промежутку ( - π; π).
Решение. Это уравнение не однородное, поэтому проведем преобразования. Число 2, содержащееся в правой части уравнения, заменим произведением 2·1
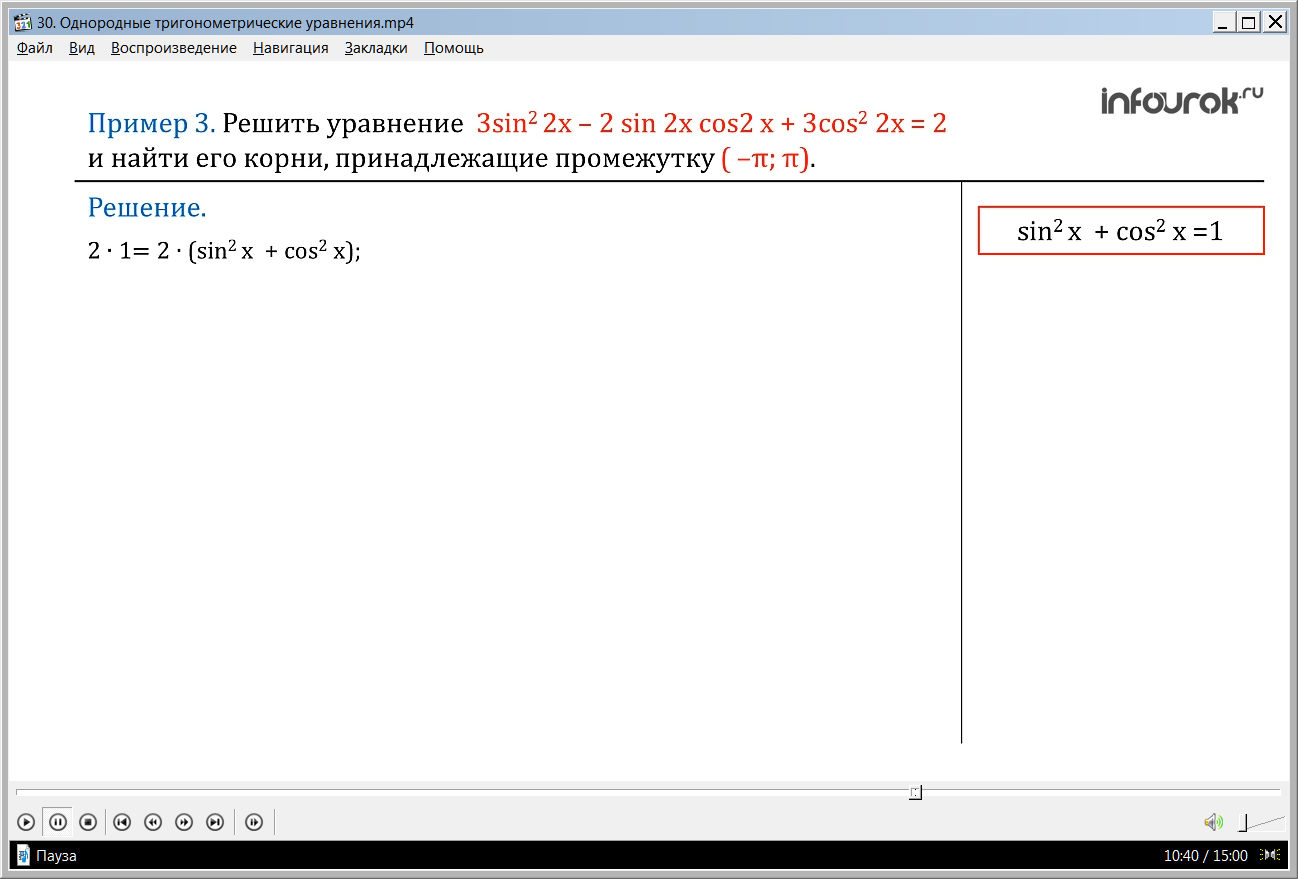
Так как по основному тригонометрическому тождеству sin2 x + cos2x =1, то
2 ∙ 1= 2 ∙ (sin2 x + cos2x) = раскрыв скобки получим: 2 sin2 x + 2 cos2x.
2 ∙ 1= 2 ∙ (sin2 x + cos2 x) =2 sin2 x + 2 cos2 x
Значит уравнение 3sin2 2x - 2 sin2xcos2 x +3cos2 2x= 2 примет вид:
3sin2 2x - 2 sin 2x cos2 x +3cos2 2x = 2 sin2 x + 2 cos2 x.
Далее все перенесем в левую часть и приведем подобные слагаемые:
3sin2 2x - 2 sin 2x cos2 x +3cos2 2x - 2 sin2 x - 2 cos2 x=0,
sin2 2x - 2 sin 2x cos2 x +cos2 2x =0.
Получили однородное тригонометрическое уравнение второй степени. Применим способ почленного деления на cos2 2x :
tg22x – 2tg 2x + 1 = 0.
Введем новую переменную z= tg2х.
Имеем z2 - 2 z + 1 = 0. Это квадратное уравнение. Заметив в левой части формулу сокращенного умножения - квадрат разности ( ), получим (z – 1)2 = 0, т.е. z = 1. Вернемся к обратной замене:
tg2х= 1,
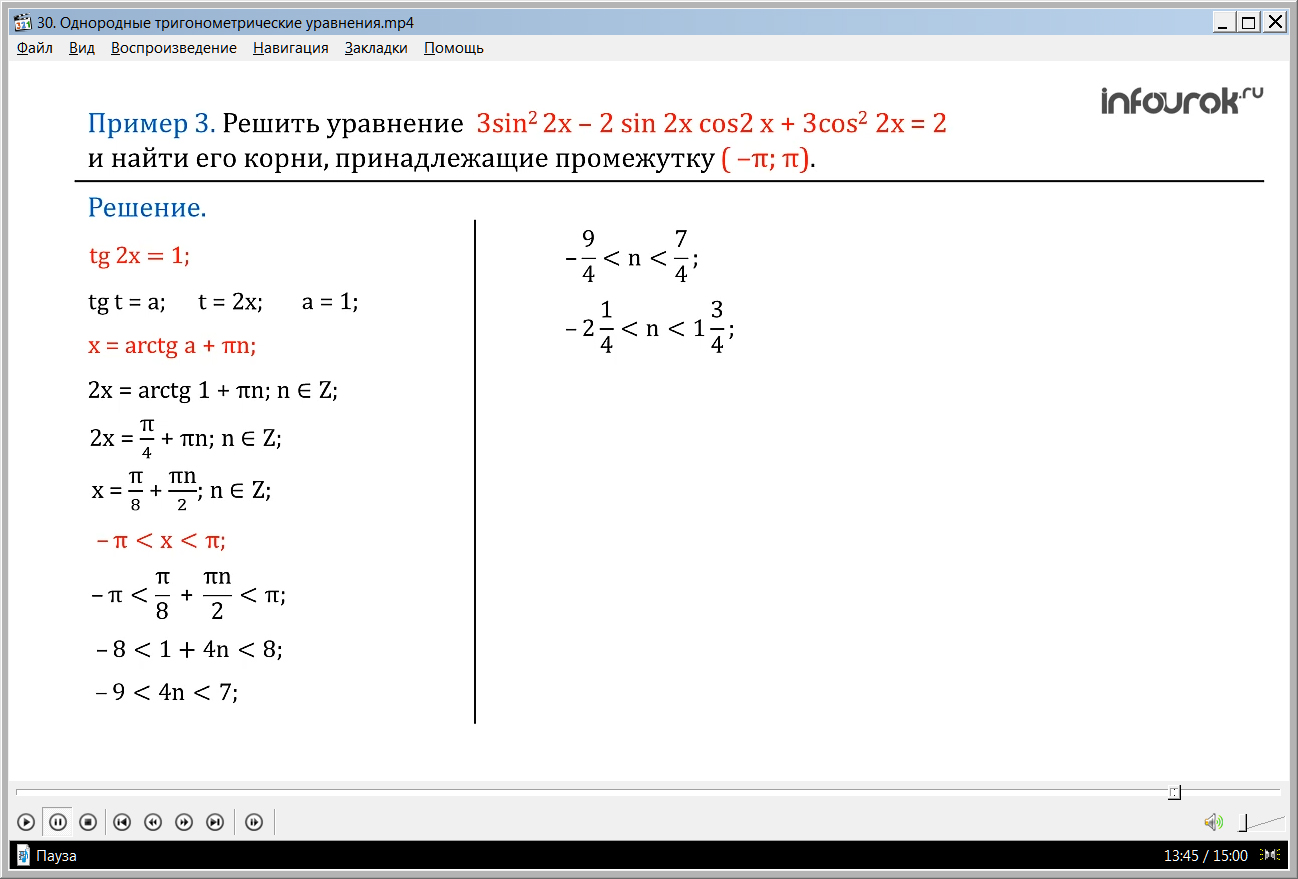
Мы привели уравнение к виду tg t = a, где t= 2х, a =1 . А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид
х = arctg x a + πn, то решение нашего уравнения будет:
2х= arctg1 + πn,
2х= + πn ,
х= + , ( икс равно сумме пи на восемь и пи эн на два).
Нам осталось найти такие значения х, которые содержатся в интервале
( - π; π), т.е. удовлетворяют двойному неравенству - π х π. Так как
х= + , то - π + π. Разделим все части этого неравенства на π и умножим на 8, получим
-8 1 + 4n 8,
перенесем единицу в право и в лево, поменяв знак на минус один
-9 4n7,
разделим на четыре получим,
для удобства в дробях выделим целые части
– <n< , так как n(эн) целые числа, то
Этому неравенству удовлетворяют следующие целочисленные n: -2, -1, 0, 1
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10574 |
| Номер материала | 858 |