
Урок "Окружность, описанная около правильного многоугольника"

Краткое описание документа:
Видеоурок «Окружность, описанная около правильного многоугольника» представляет наглядный учебный материал по данной теме. Рассматривается формулировка теоремы о возможности описания многоугольника окружностью, а также доказательство данной теоремы. Задачей данного видеоурока является понятное удобное представления теоремы и доказательства, чтобы облегчить усвоение материала учениками при изучении темы. При помощи данного видеоурока учитель имеет возможность освободить время урока для улучшения индивидуальной работы. Видеоурок помогает более быстрому достижению учебных задач, повышает эффективность урока.
В ходе видеоурока используются приемы, которые дают возможность влиять на запоминание материала учениками, удерживать внимание на предмете изучения. При помощи анимации произведенные построения приближены к традиционной демонстрации на доске, однако при этом хорошо видны с любой парты, четкие, понятные, не требуют вспомогательных инструментов.
Начинается видеоурок с представления темы. На момент изучения темы ученики уже знакомы с понятием окружности, которая описывает многоугольник. Диктор напоминает ученикам, что она является окружностью, на которой лежат вершины многоугольника. Далее демонстрируется доказательство теоремы об описанной окружности правильного многоугольника. Выводится формулировка теоремы о возможности описать такую окружность, и только одну.
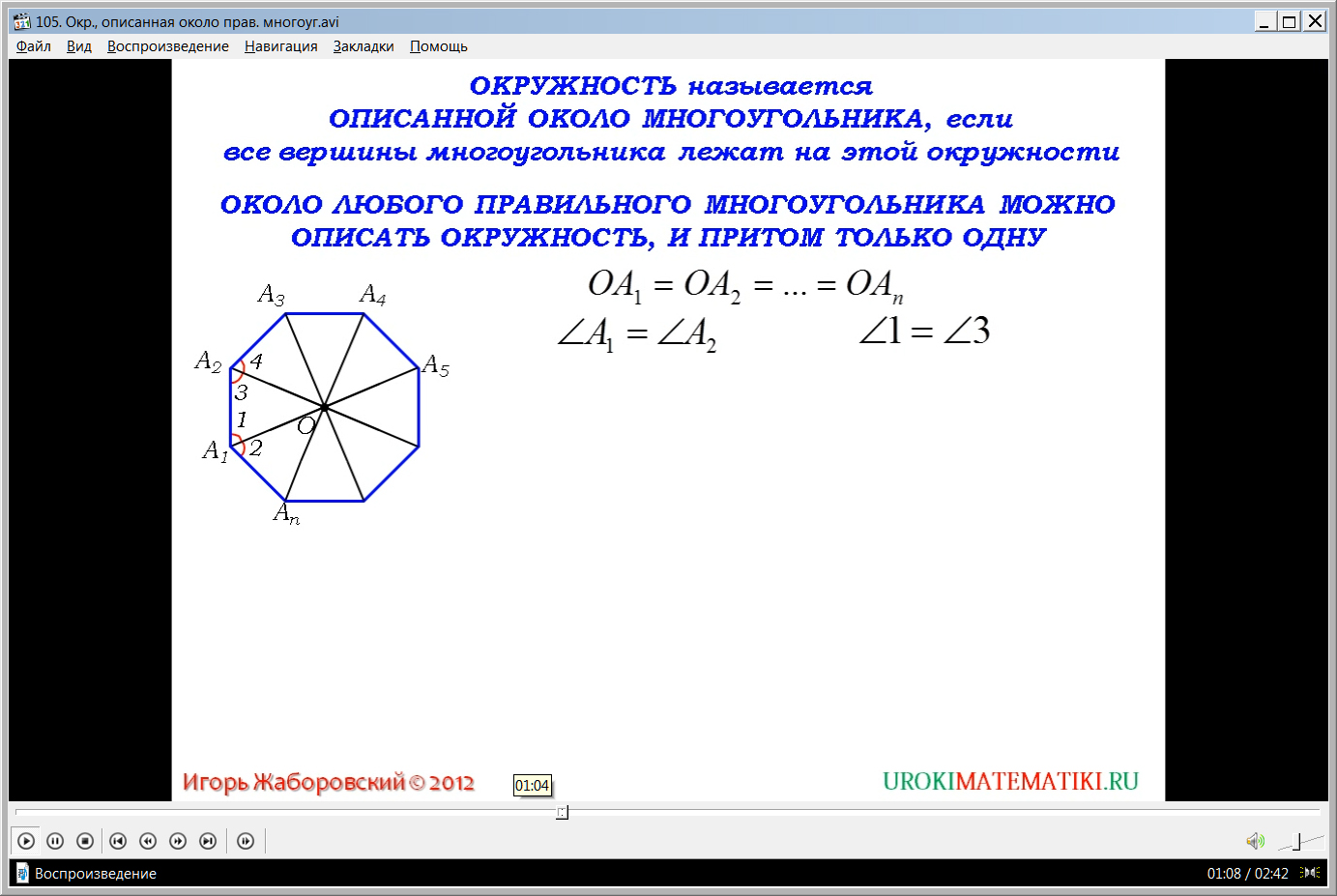
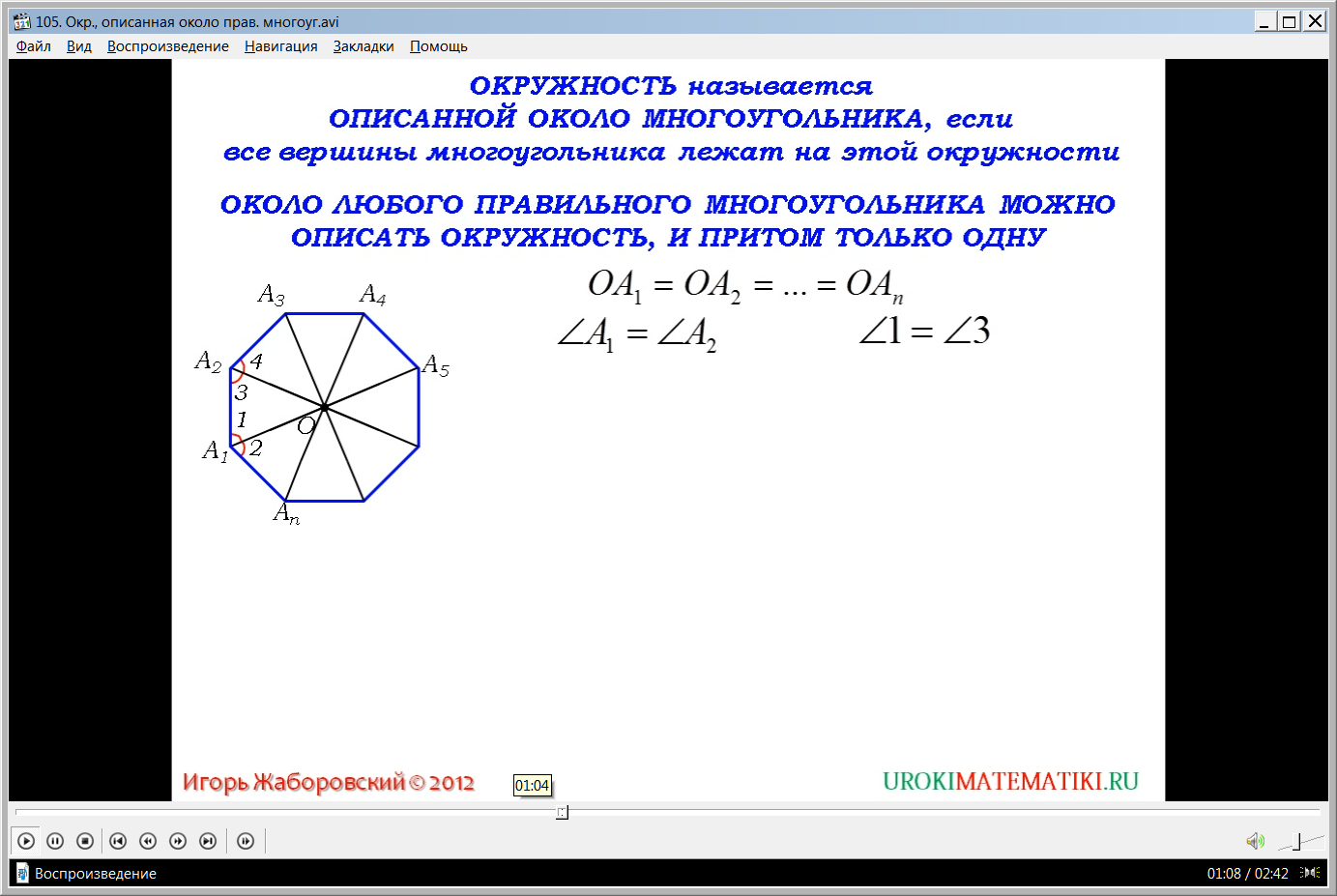
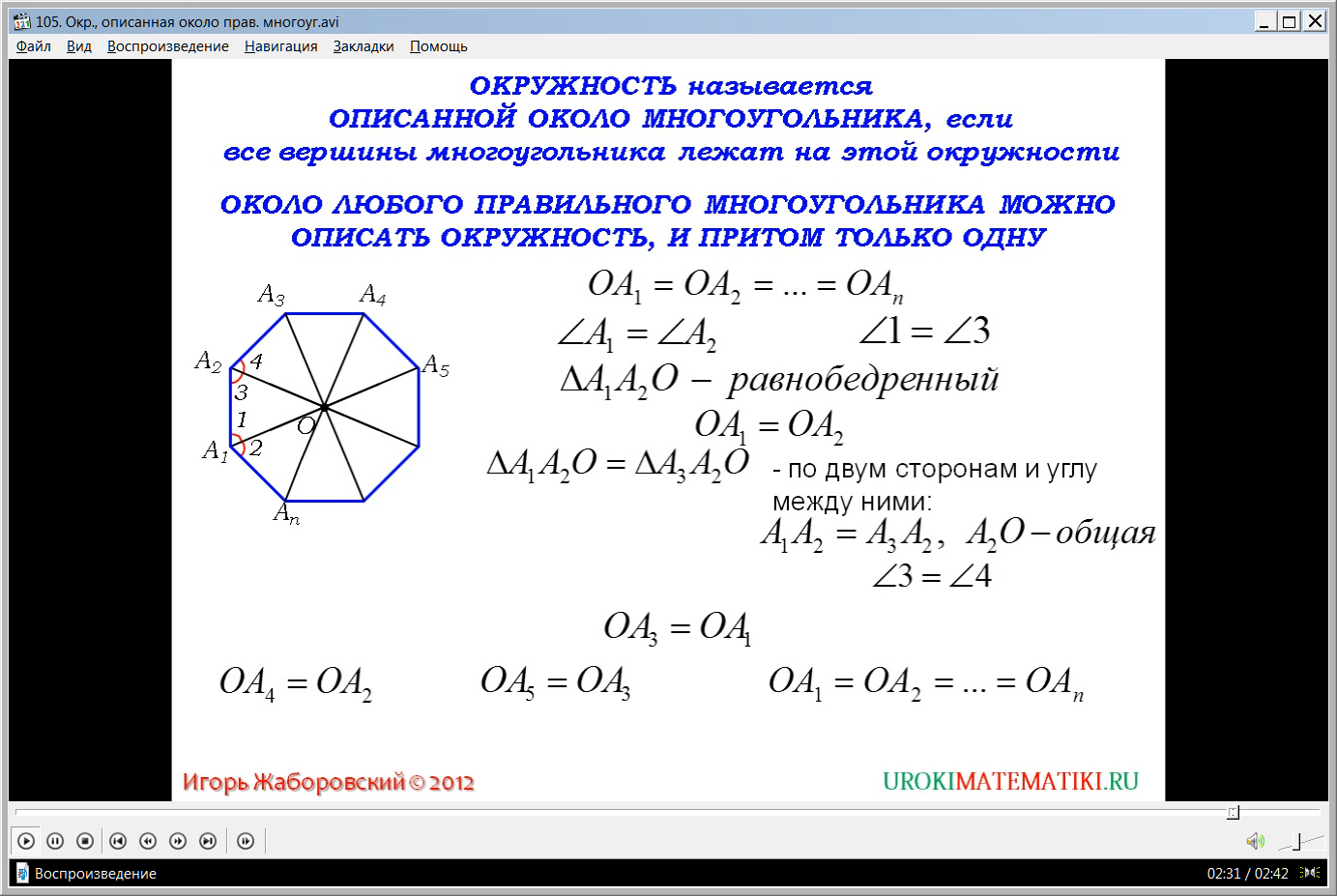
Описываемое доказательство начинается с построения многоугольника. На экране изображается правильный восьмиугольник, из двух вершин которого А1 и А2 проводятся биссектрисы углов. Отмечается точка пересечения биссектрис. От образованной таким образом точки О проводятся к другим вершинам ОА3, ОА4 и т.д. Необходимо доказать равенство ОА1= ОА2=…= ОАn. Из определения правильного многоугольника следует, что углы А1 и А2 равны. Это означает, что и углы, на которые их делит биссектриса, также равны. Поэтому отмеченные на рисунке углы 1 и 3, образованные биссектрисами, равны. Это говорит о том, что образованный в результате построения треугольник А1ОА2, является равнобедренным, а это значит, что ОА1=ОА2. Образованный таким образом треугольник А2ОА3 равен треугольнику А1ОА2 по углу и двум сторонам. Это следует из того, что ОА2 является общей стороной, А1А2 = А2А3 равны (из определения правильного n-угольника), образованные биссектрисами углы 3 и 4 также равны согласно построению. Из равенства рассматриваемых треугольников следует равенство сторон ОА1= ОА2. Аналогично рассуждая, можно доказать равенство остальных сторон треугольников , а это значит ОА1= ОА2=…= ОАn. Доказано, что точка О является равноудаленной от точек, являющихся вершинами многоугольника. Это значит, что можно построить описанную окружность правильного n-угольника.
Вторая часть доказательства – необходимо доказать единственность описанной окружности. Для этого предлагается описать три вершины – к примеру, А1, А2, А3. Отмечается, что через эти вершины строится единственная окружность. Следовательно, и через все вершины произвольного n-угольника описывается единственная окружность.
Видеоурок «Окружность, описанная около правильного многоугольника» рекомендуется использовать в качестве наглядного пособия или части урока на традиционных занятиях в школе. Также данное пособие рекомендуется ученикам, которые решили освоить тему самостоятельно или требуют более глубокого понимания предмета. Видеоурок может стать эффективным инструментом учителя, проводящего дистанционное обучение.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6884 |
| Номер материала | 755 |