
Урок "Описанная окружность"

Краткое описание документа:
Окружность является одной из наиболее востребованных геометрических фигур. Она широко используется в ряде математических задач различного характера и направления. В частности, целый раздел геометрии посвящен описанным окружностям. В представленном видео уроке будет проведен тщательный анализ свойств данного геометрического объекта.
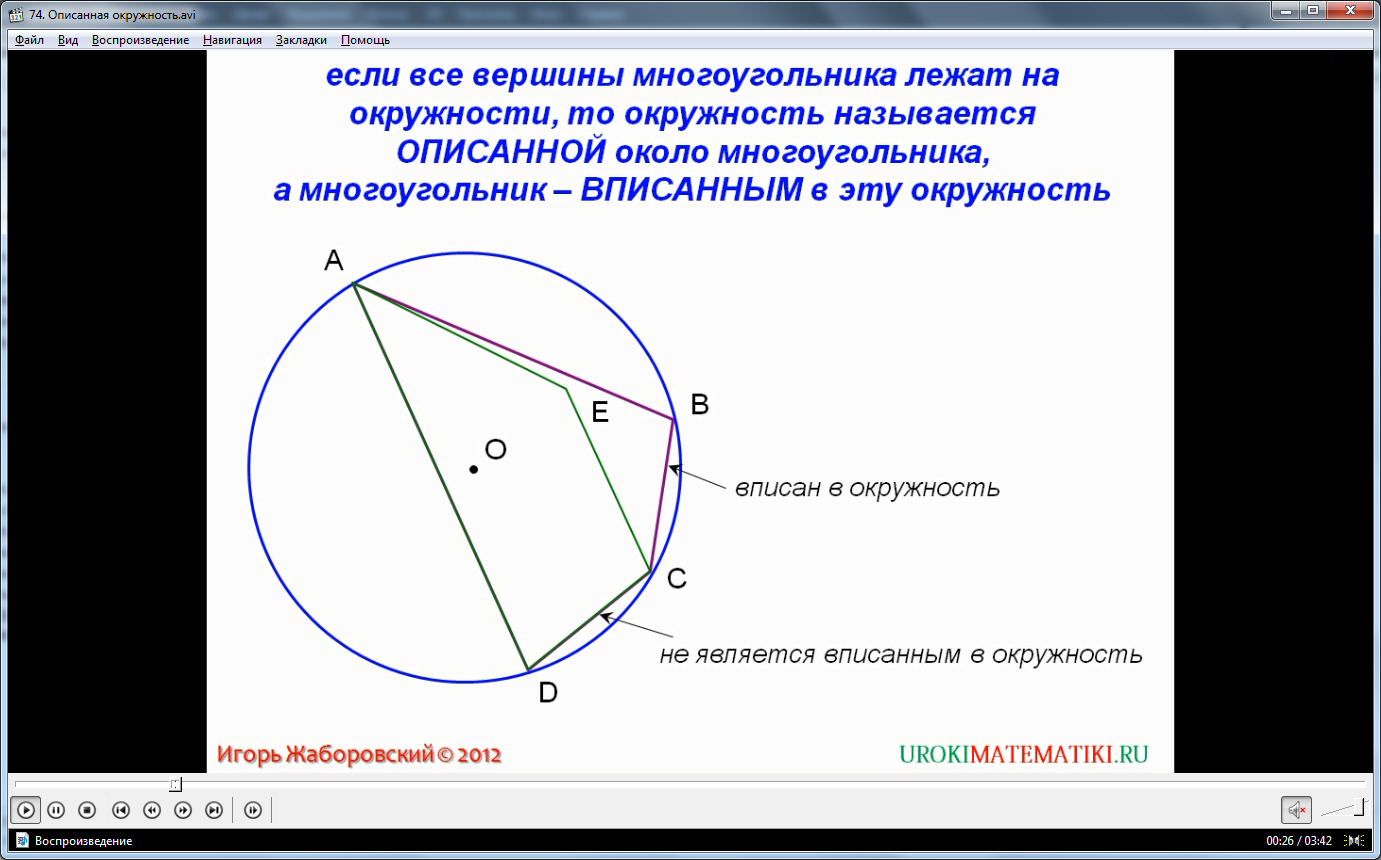
Описанная окружность – это некая окружность, содержащая все вершины определенного выпуклого многоугольника. Стоит отметить, что некоторые экзотические невыпуклые правильные фигуры, например, звезда, тоже могут быть описаны окружностью, но, при этом, будут затронуты далеко не все вершины звезды.
Видео прекрасно иллюстрирует различные виды многоугольников, описанных окружностью. Этот элементарный процесс имеет свои правила и некоторые свойства, на которых стоит остановиться подробнее.
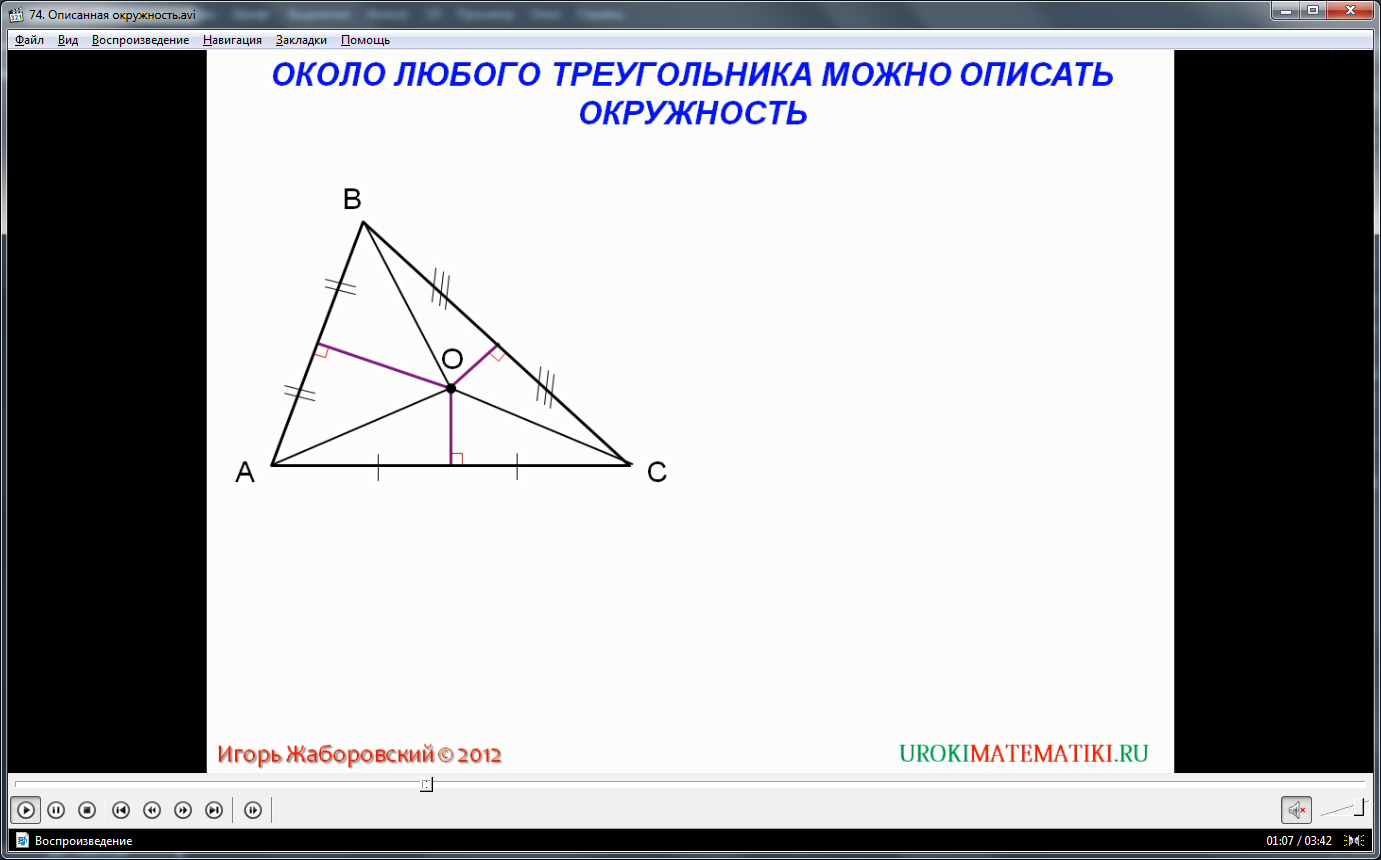
Первый закон описанной окружности гласит, что её центр, точка пересечения любых диаметров, является также центром пересечения всех срединных перпендикуляров многоугольника. Напомним, что срединный перпендикуляр – это линия, проведенная под прямым углом из геометрического центра какой-либо стороны фигуры.
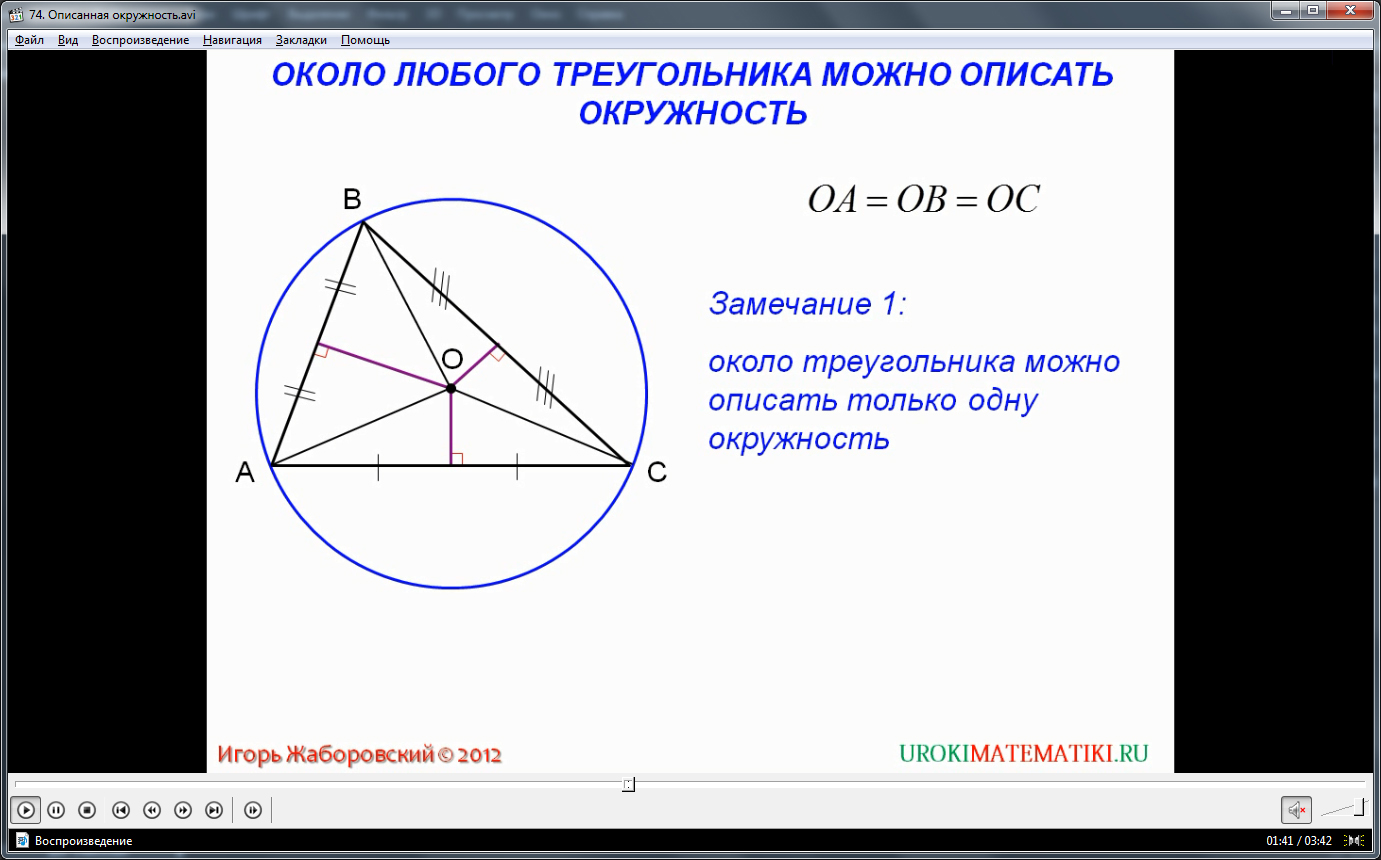
Возможность описания фигуры окружностью зависит от многих факторов. Например, описать можно абсолютно любой треугольник. Кроме того, описываются все правильные многоугольники, у которых равны стороны и углы, при этом вариант пролегания окружности для них исключительно один.
Для описанных треугольников существуют определенные свойства, характеризующие зависимости от величины углов фигуры. Например, у тупоугольного треугольника центр окружности лежит за пределами самой фигуры. У остроугольного – на площади фигуры. А у прямоугольного треугольника центр описанной окружности располагается строго посередине гипотенузы.
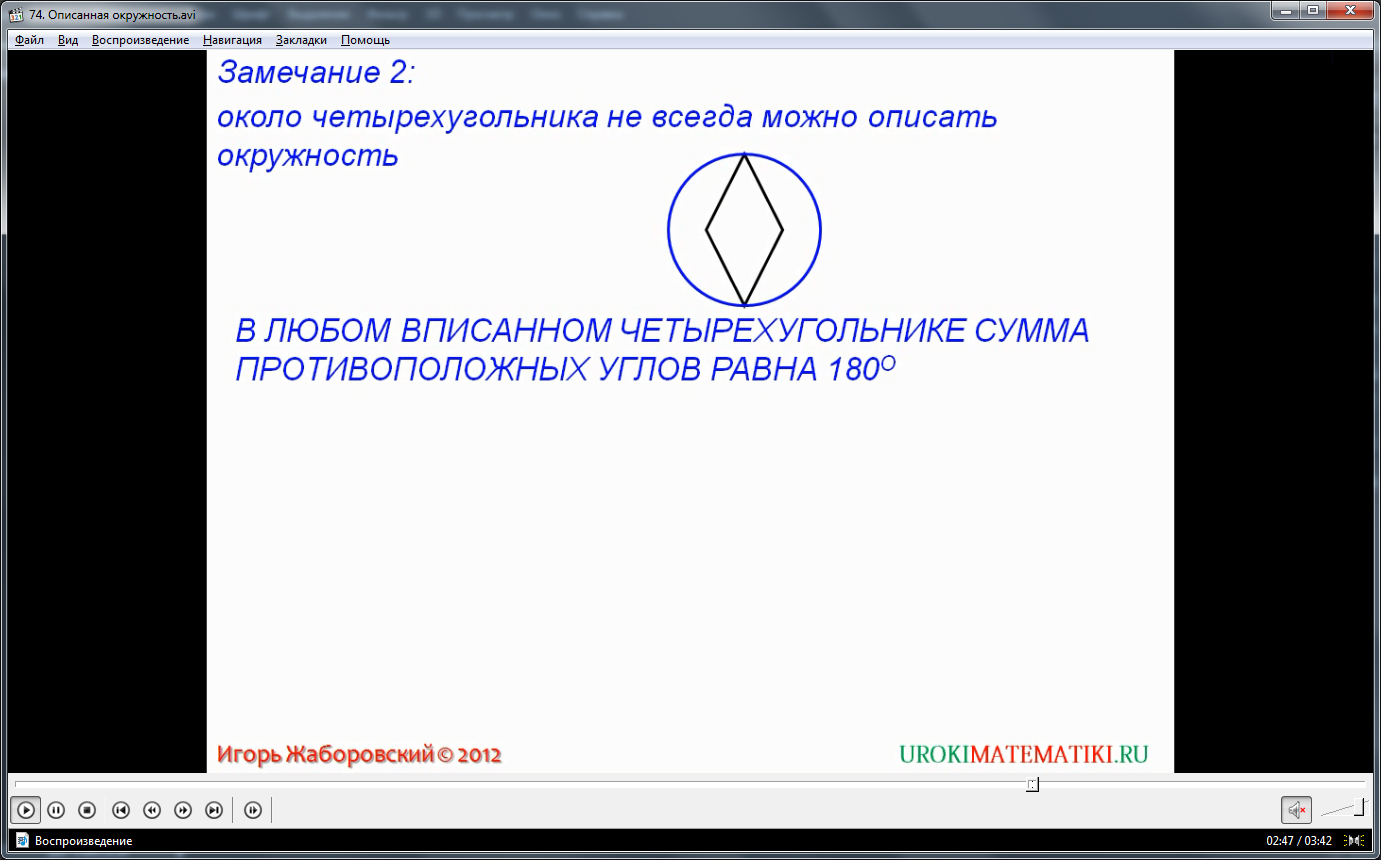
Для любого вписанного четырехугольника верно правило: противоположные углы фигуры равны в сумме 180 градусам. Иначе фигуру с четырьмя углами невозможно описать окружностью. Для многоугольников с большим количеством углов, суммы углов могут быть и больше. На практике, чаще всего пользуются обратным следствием из этого правила – а именно, подтверждают, или опровергают возможность описания четырехугольника, путем вычисления его противоположных углов и анализа их сумм.
Для любых многоугольников, как подтверждает нам наглядная видео иллюстрация, работают следующие правила:
- Если из произвольного количества отрезков произвольной длины, реально существующих в эвклидовом пространстве, составить многоугольник максимально возможной площади, то его можно легко описать окружностью.
- Если рассмотреть некую точку, равноудаленную от вершин, лежащую внутри многоугольника, то она будет точно совпадать с центром описанной окружности.
Данные правила имеют достаточно сложные доказательства, растущие из определений и основных законов окружности. Поэтому мы не будем их доказывать, просто воспользуемся ими для решения практических задач.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5123 |
| Номер материала | 612 |