
Урок «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии»

Краткое описание документа:
Видеоурок «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии» является наглядным пособием для ведения урока алгебры по данной теме. Видеоматериал вводит понятие арифметической прогрессии, учит отличать арифметическую прогрессию в ряде различных последовательностей чисел, дает представление об основных формулах, которые задают член арифметической прогрессии, учит применять их для решения задач, связанных с арифметической прогрессией. Задача данного видеоурока – облегчить усвоение материала, помочь ученикам запомнить основные формулы, необходимые для решения задач, формировать умение применять полученные знания в решении задач.
Основными инструментами видеоурока являются анимационные эффекты, различные приемы выделения понятий, голосовое объяснение материала. При помощи анимационных эффектов удерживается внимание учеников на изучении материала, наглядные материалы структурируются, подаются в удобном виде. При помощи выделения облегчается запоминание и усвоение учебного материала.
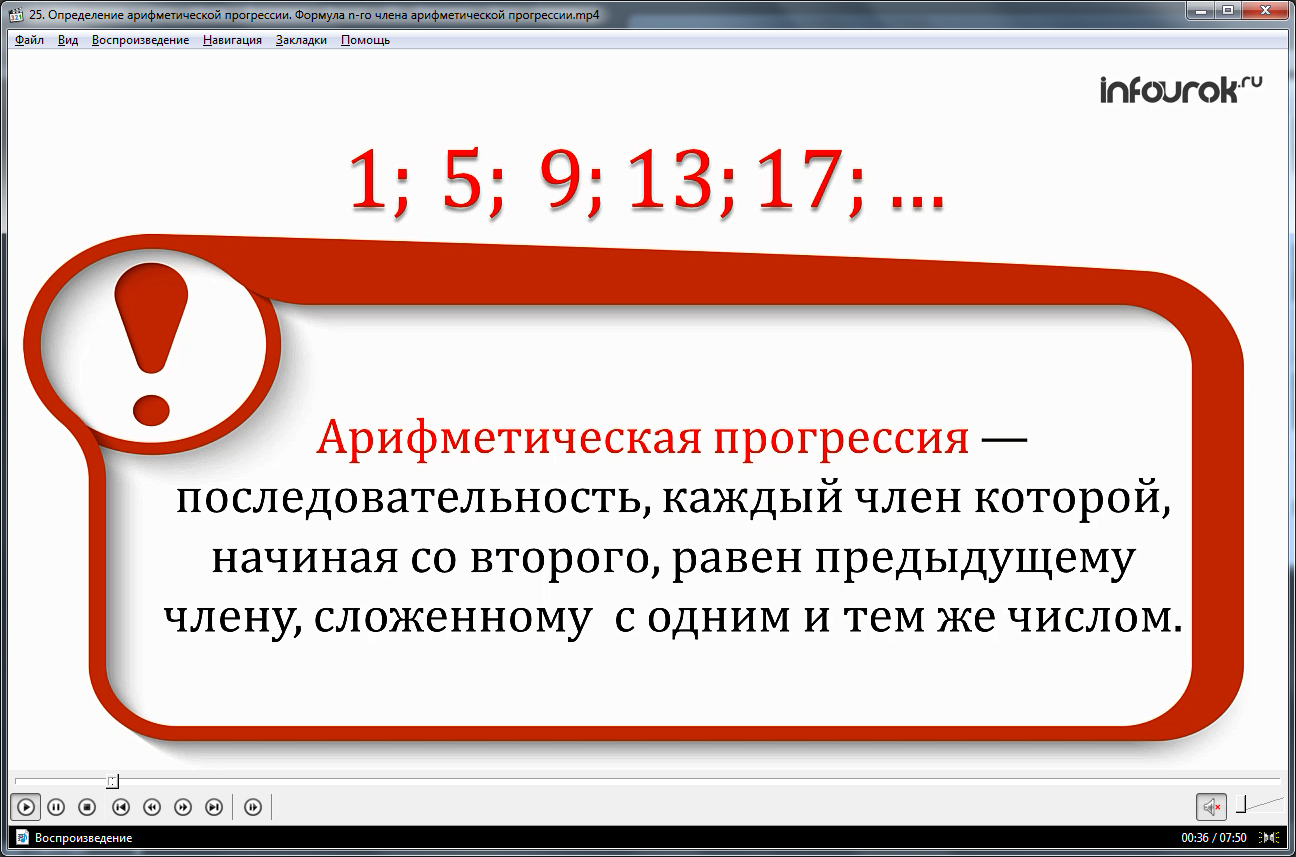
Вначале представляется тема видеоурока. Приводится пример последовательности некоторых чисел 1, 5, 9, 13, 17, …, указывая на то, что любой ее член, больший первого, равняется предыдущему, сложенному с 4. Отмечается, что подобные последовательности, всякий член которых образуется сложением с некоторым числом, являются арифметической прогрессией.
Далее демонстрируется математическая запись основного условия, определяющего арифметическую прогрессию. Она указывает, что (an) будет арифметической прогрессией, когда для всякого натурального n выполняются условия, описанные в формуле ее члена: an+1= an+d с некоторым числом d. Вводится понятие разности арифметической прогрессии, являющейся разностью между любым членом и предыдущим перед ним. Это некоторое число, одинаковое для всякой разности рядом стоящих членов последовательности: an+1-an=d.
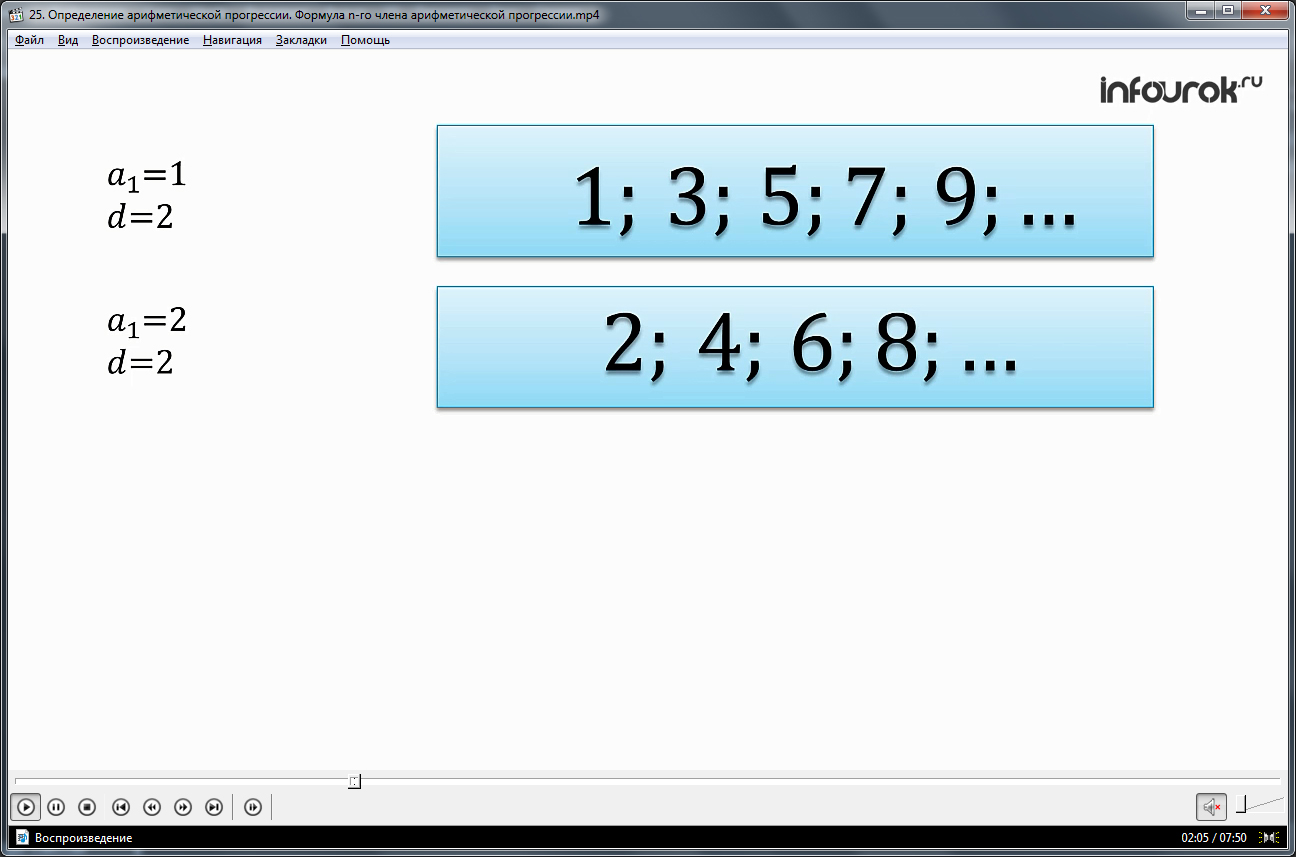
Описываются примеры арифметической прогрессии, определенной первым членом, а также разностью. Отмечается, что арифметическая прогрессия для а1=1 и d=2 будет 1, 3, 5 ...; арифметическая прогрессия, где а1=2 и d=2 представляет собой последовательность чисел 2, 4, 6 и т.д. Пример прогрессии с разностью d= -1 и а1=-1 будет -1, -2, -3 и т.д. Для прогрессии с первым членом 5, разностью 0 она будет рядом одинаковых чисел 5, 5 и т.д. Отмечается, что таким образом можно найти всякий член арифметической прогрессии, однако такой способ вычисления неудобный. Есть более эффективный метод нахождения члена арифметической прогрессии.
Описание формулы n-ного члена начинается с ее выведения. Для этого второй член прогрессии представляется как а2=а1+d, третий – а3=а2+d=(а1+d)+d=а1+2d, а4=(а1+2d)+d=а1+3d и т.д. Соответственно, найти значение некоторого n-ного члена указанной арифметической прогрессии можно, применяя формулу an=a1+d(n-1). Она выведена в рамку для запоминания и записи в тетради.
Разбирается пример вычисления члена последовательности – самое простое задание. Дана последовательность (cn), которая задана первым членом c1=0,2 и разностью d=0,4. Используем для нахождения 40-го члена последовательности известную формулу: c40=0,2+0,4(40-1)=15,8.
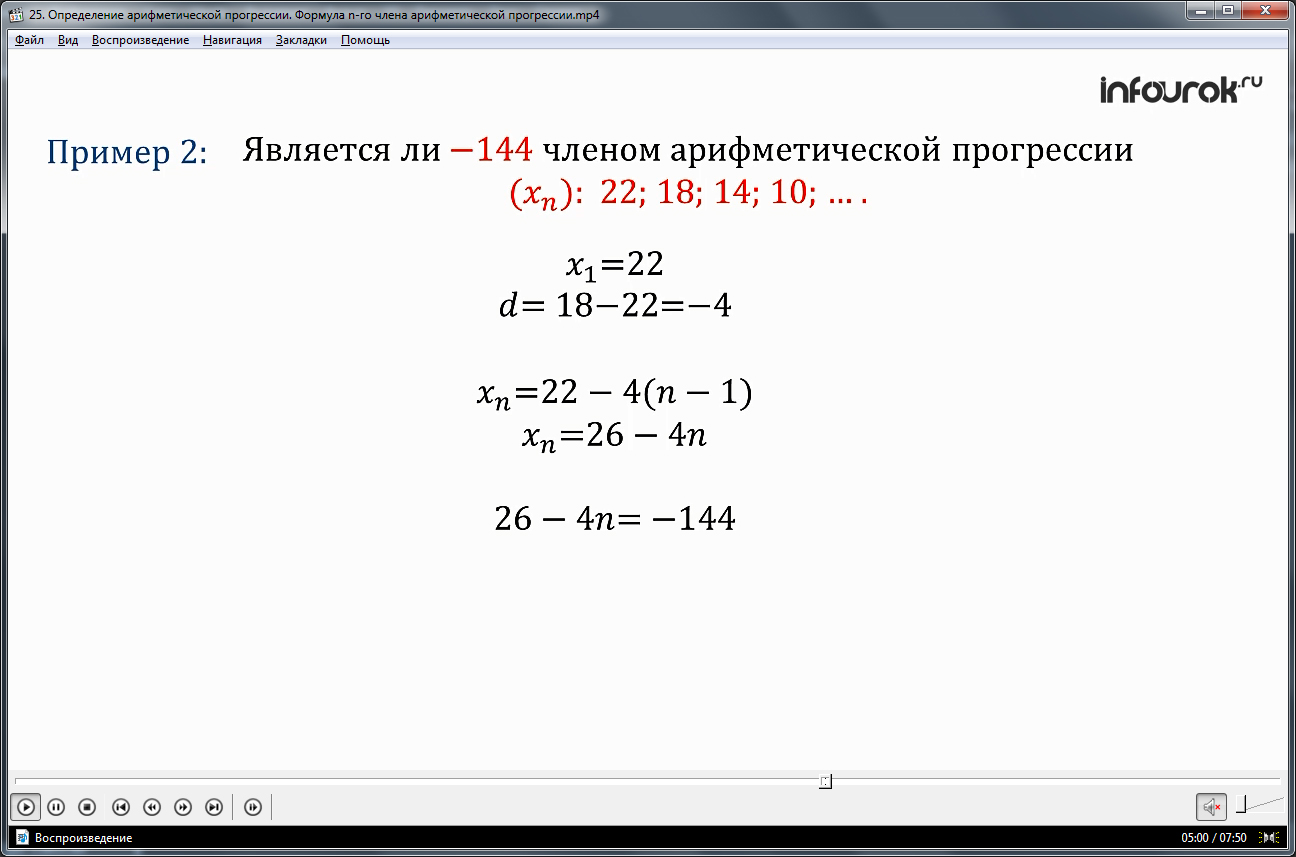
При решении следующего примера рассматривается более сложное задание – выяснить, является ли указанное число членом прогрессии. Арифметическая прогрессия (xn) задается последовательностью чисел 22, 18, 14, 10,…Определяем, что первым членом является xn=22, а разностью d=18-22=-4. Поэтому формула, определяющая некоторый член прогрессии, формулируется так: xn=22-4(n-1). Иначе xn=26-4n. Чтобы -144 было часть. Данной последовательности, необходимо, чтобы оно удовлетворяло условию: 26-4n=-144. Решив данное уравнение, обнаруживается, что n=42,5, то есть оно не является натуральным числом. А значит, число -144 не является членом прогрессии.
Рассматривается еще одна закономерность, которая важна при решении задач, связанных с арифметическими прогрессиями. Всякий член некоторой арифметической прогрессии, больший первого, можно вычислить как среднее арифметическое от предыдущего и последующего. Оно доказывается просто, что и демонстрируется на экране. Для арифметической прогрессии an, вычисленная разность члена с предыдущим равна разности последующего с данным членом: an- an-1= an+1- an. После перегруппировки членов равенства получаем 2an= an-1+ an+1. Иначе это можно записать an=( an-1+ an+1)/2, что подтверждает утверждение.
Также доказывается справедливость обратного утверждения о том, что равенство каждого члена среднему арифметическому предыдущего и последующего членов означает, что она – арифметическая прогрессия. Преобразуя формулу n-го члена an=(an-1+ an+1)/2 с n>=2, получаем 2an= an-1+ an+1, или an- an-1= an+1- an, что доказывает утверждение.
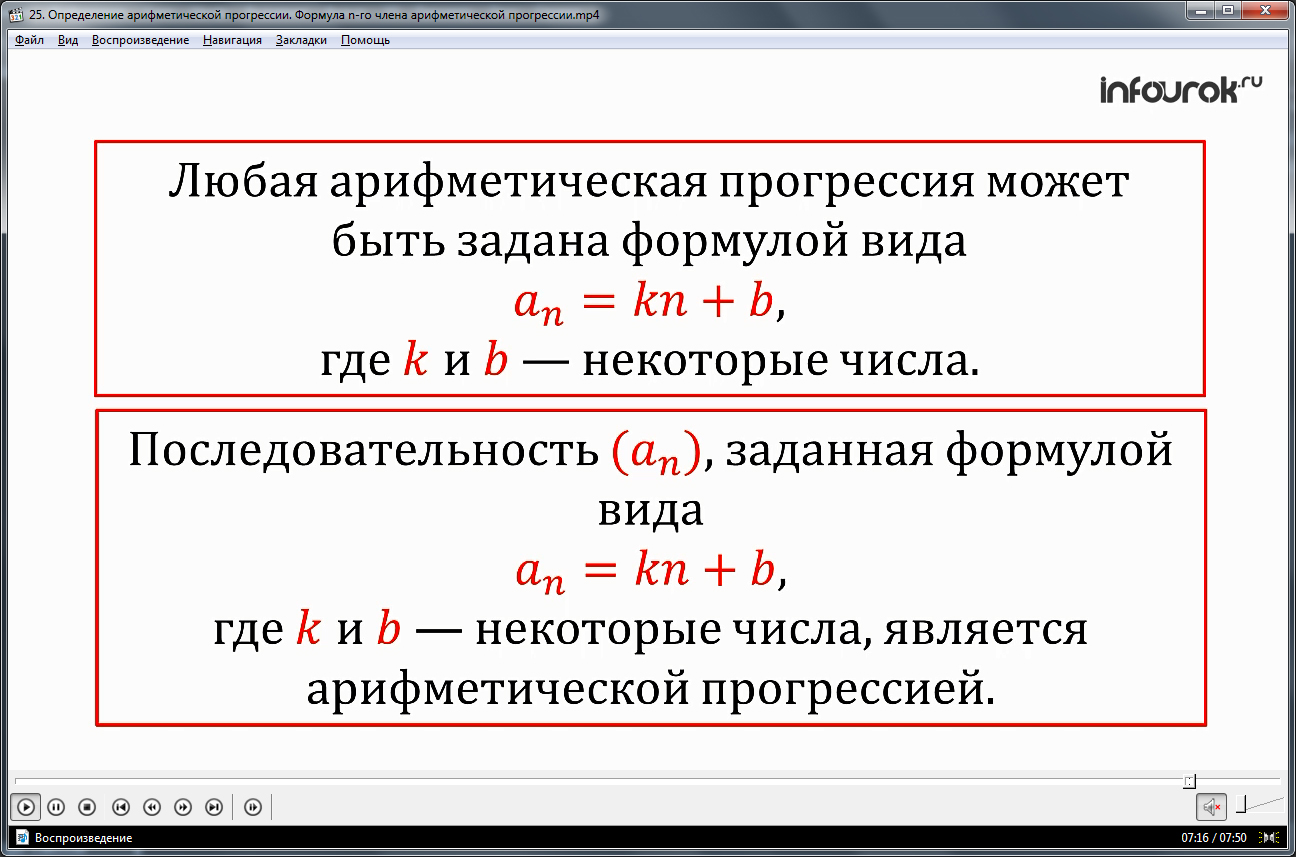
Также рассматривается еще один аспект формулы n-го члена. Отмечается, что ее можно представить в виде an=dn+(a1-d). Такое представление дает право утверждать, что всякая арифметическая прогрессия задается формулой an=kn+b, в которой k и b – некоторые числа. Также верно обратное утверждение, которое определяет как арифметическую прогрессию некую последовательность, задаваемую формулой an=kn+b с числами k и b. Подтверждается это при помощи подстановки формулы в выражение для нахождения разности арифметической прогрессии. an+1-an= k(n+1)+b-(kn+b)= kn+k+b-kn-b=k. Отсюда еще один вывод, что для всякого n верно an+1=an+ k. Данная последовательность an будет арифметической, а ее разность k.
Видеоурок «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии» подробно разъясняет понятие арифметической прогрессии, представляет все важные формулы n-го члена, и следующие их них, для решения задач. Данный материал также будет полезен при дистанционном обучении. Наглядное пособие поможет ученикам и в самостоятельном освоении материала.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7512 |
| Номер материала | 669 |