
Урок «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»

Краткое описание документа:
Видеоурок «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии» дает представление о геометрической прогрессии, ее элементах, формирует умения решать задачи, в которых используются геометрические прогрессии. Задача данного видеоурока – представить учебный материал в наглядном виде, повысить эффективность обучения на уроках математики.
В видеоматериале используются элементы, помогающие удерживать внимание учеников на изучаемом материале, помогать запоминать понятия и определения, способствовать глубокому пониманию материала. Такими инструментами являются анимационные эффекты, выделение цветом, заключение важных материалов в рамки для запоминания и записи в тетради.
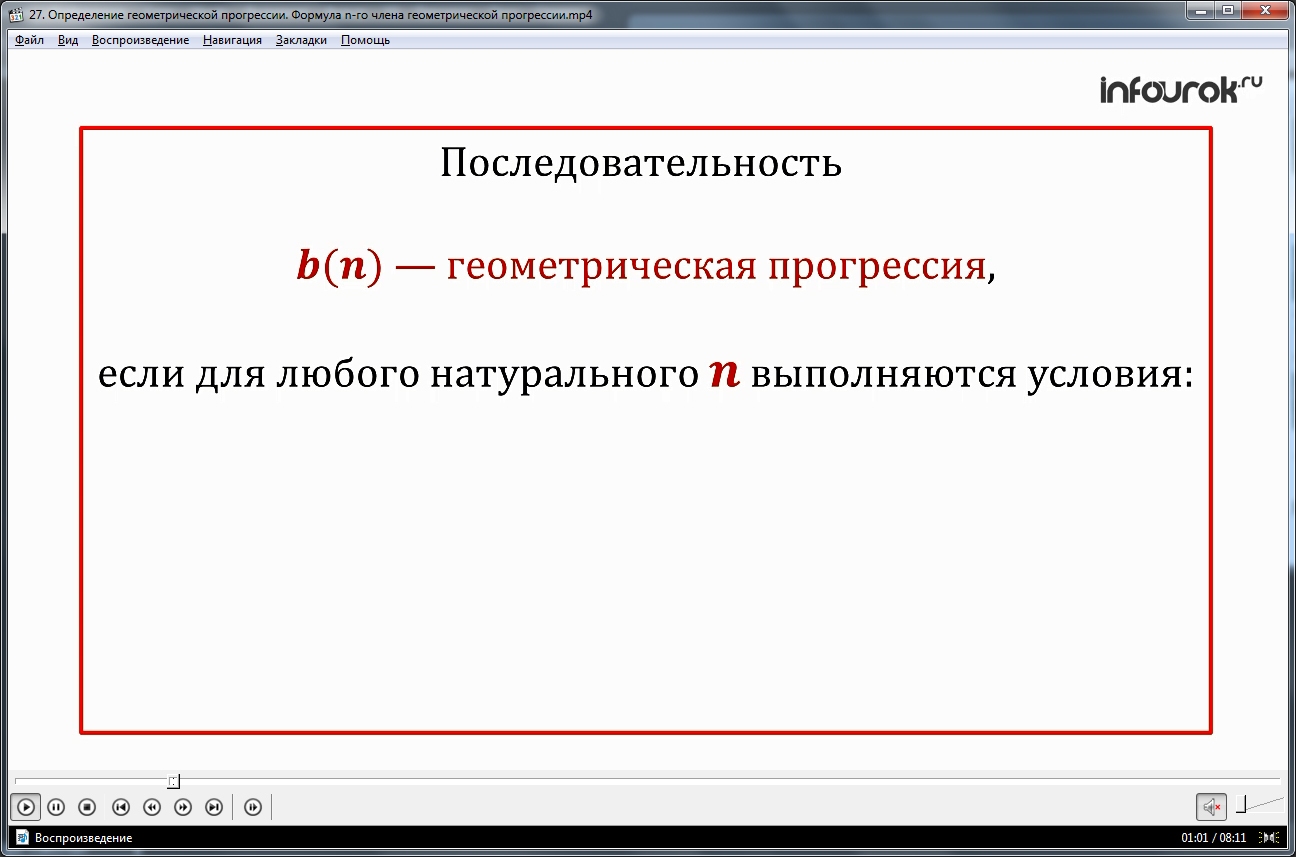
Урок начинается с представления темы. Вначале предлагается рассмотреть последовательность чисел, которые представляют собой степень с одинаковым основанием и показателем степени. Возрастающем с каждым членом на единицу: 2, 22, 23, 24… Отмечается, что каждый член данной прогрессии, кроме первого, образован умножением на 2 предыдущего члена. Такая последовательность называется геометрической прогрессией. Название прогрессии выделено для запоминания в рамку. Далее демонстрируется определение геометрической прогрессии, которая представляет собой последовательность чисел, не равных нулю, которые образуются умножением предыдущего члена на некоторое одно и то же число, начиная со второго члена. На следующем кадре представлен общий вид геометрической прогрессии (bn), которая определяется тем, что для каждого натурального nбудет bn≠0, а bn+1= bn·q, где q – некоторое число. Рассматривается, каким образом определяется геометрическая прогрессия, описанная в начале урока 2, 22, 23, 24… Если данную последовательность обозначить через (bn), то ее каждый член, больший первого, можно представить равенством bn+1= bn·2. Число q, на которое умножается каждый член прогрессии, здесь равняется 2.

Далее вводится понятие знаменателя геометрической прогрессии, который равен уже выделяемому числу q. Для этого указывается, что при делении любого члена геометрической прогрессии на предыдущий член bn+1/bnполучается данное число q, которое неравно 0. Оно и является знаменателем прогрессии. Задание некоторой геометрической прогрессии сводится к указанию ее первого члена и знаменателя.
Приводятся примеры, в которых необходимо определить геометрическую прогрессию, в которой указаны первый член и знаменатель. Описывается геометрическая прогрессия 1; 0,1; 0,01; 0,001; 0,0001,… с первым членом b1=1 и q=0,1, прогрессия с первым отрицательным членом b1=-4 и знаменателем q=3: -4; -12; -36;…, прогрессия с отрицательным знаменателем q=-2 и первым членом b1=6: 6; 6;…
На основе рассмотренных примеров делается обобщение, каким образом можно найти любой член геометрической прогрессии: b2= b1q, b3= b2q= b1q2 и т.п. Из данных формул видно, что следующий член образуется умножением первого на qn-1. На экран выводится формула bn=b1qn-1. Отмечается, что данная формула есть формулой n-го члена геометрической прогрессии, ее необходимо запомнить, так как она далее будет использоваться в решении задач.
Рассматривается пример, в котором описывается нахождение 5-го члена геометрической прогрессии, в которой первый член b1=8 и знаменателем прогрессии является q=1/2. Напоминается изученная формула n-го члена, которая для 5-го члена будет звучать таким образом: b5=b1q5-1. После подстановки чисел, являющихся значениями первого члена и знаменателя, вычисляется 5-й член прогрессии: b5=8·(1/2)4=1/2.
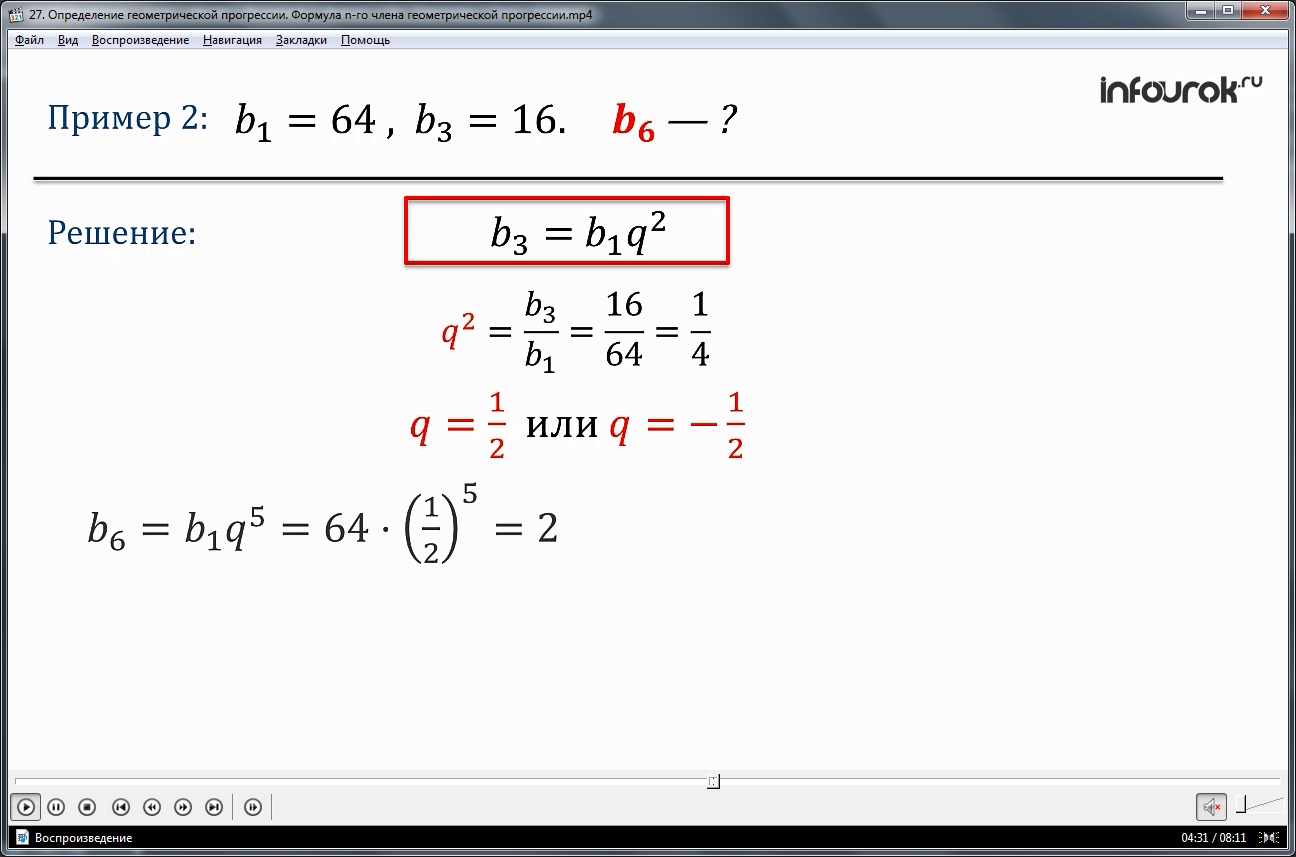
Второй пример демонстрирует нахождение 6-го члена геометрической прогрессии, в которой известен первый и третий члены: b1=64 и b3=16. Для поиска третьего члена прогрессии формула приобретает вид: b3=b1q2. Зная, что каждый следующий член образуется умножением предыдущего на знаменатель, определяем квадрат знаменателя q2= b3/b1=16/64=1/4. Очевидно, что q может принимать значения ½ или -1/2. Решение сводится к вычислению значения 6-го члена в случае, когда знаменатель равен ½ и -1/2. В первом случае b6=b1q5=64·(1/2)5=2, а во втором b6=b1q5=64·(-1/2)5=-2. Поэтому значение 6-го члена может быть 2 или -2.
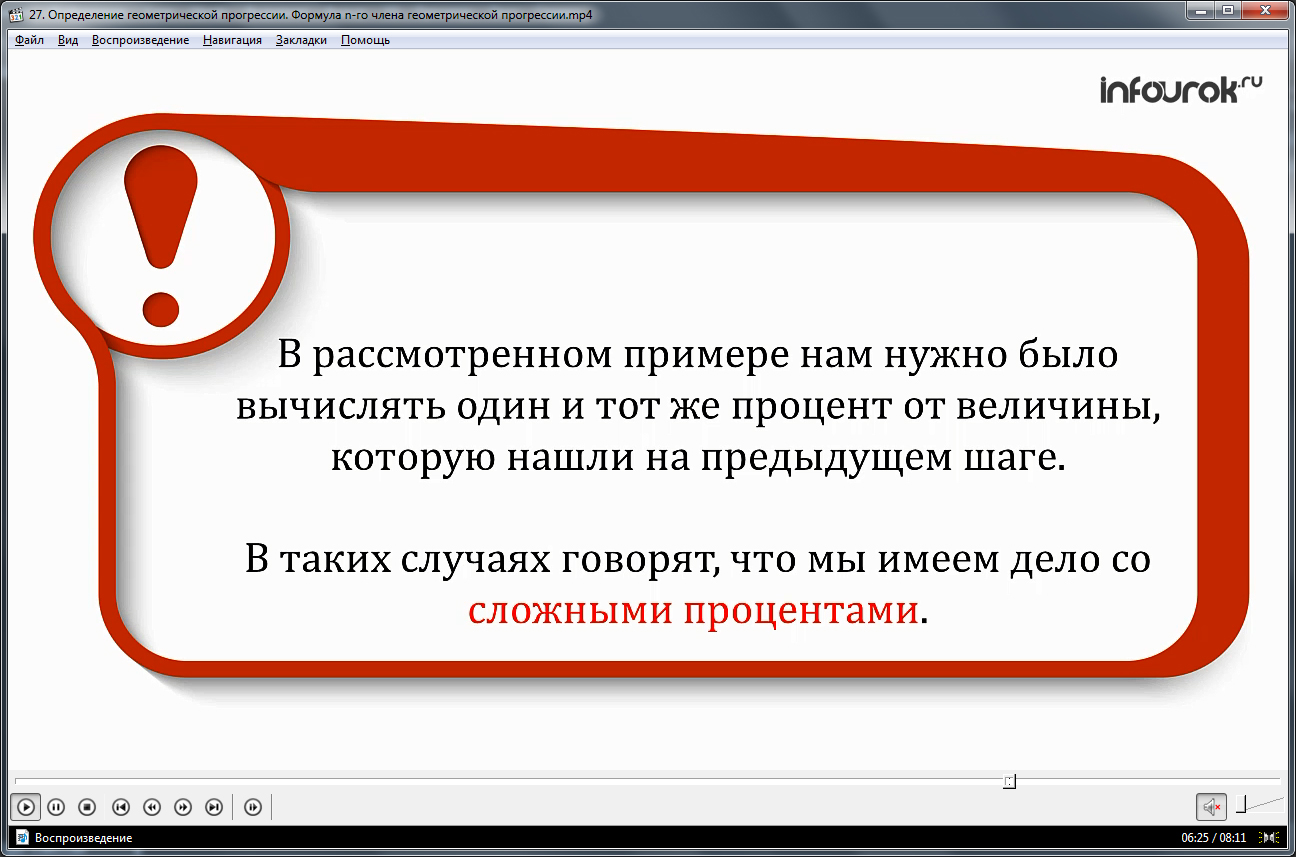
Демонстрируется пример, каким образом используются математические знания о геометрической прогрессии в решении практических задач. Предлагается рассмотреть решение задачи о возрастании суммы банковского вклада за 5 лет, если процент роста составляет 4%, а начальная сумма 6000 рублей. Так как рост вклада за первый год составит 4%, то сумма будет 6000·1,04 р., значение этой суммы за два года будет составлять (6000·1,04)·1,04 или 6000·1,042. Таким образом мы получаем геометрическую прогрессию, в которой каждый последующий член умножается на 1,04. Она будет состоять из чисел 6000, 6000·1,04; 6000·1,042; … Накопления, которые будут на счете через 5 лет, представляют собой 6-й член геометрической прогрессии. По формуле b6=b1q5 находим его значение 6000·1,045≈7300. Это и будет приближенным значением суммы. Задачи подобного типа называются задачами со сложными процентами. Они нередко появляются в экономике, банковском секторе.
На экран для запоминания выведено еще одно полезное правило. Оно утверждает, что квадрат любого члена геометрической прогрессии, кроме первого, будет равен произведению предыдущего и последующего членов. Данное утверждение подтверждается, если рассмотреть некоторую прогрессию (bn). В ней n-й член равен bn= bn-1q. А n+1-й член определяется bn+1= bnq. Так как все члены геометрической прогрессии не равны нулю, можно их представить отношением bn/bn-1=bn+1/bn. Отсюда значение квадрата будет bn2= bn-1·bn+1. Также отмечается, что к данному утверждению верно и обратное. То есть равенство произведения предыдущего и последующего членов квадрату данного члена означает, что эта последовательность – геометрическая прогрессия.
Обращается внимание учеников на то, что модуль любого члена геометрической прогрессии является средним геометрическим последующего и предыдущего членов. Это подтверждается простой демонстрацией: bn2=bn-1·bn+1, следовательно, | bn|=√(bn-1·bn+1).
Видеоурок «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии» может быть использован как наглядный материал или полноценная часть урока в школе. Он хорошо раскрывает данную тему, поэтому может быть полезен для самостоятельного изучения, может быть полезен в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 14560 |
| Номер материала | 671 |