
Урок "Определение и задание обратной числовой функции"

Краткое описание документа:
Темам «Функции» и «Исследование функций» в курсе 10 класса уделяется много внимания. Не остался в стороне и урок «Определение и задание обратной числовой функции». Как и любая другая тема по математике, этот урок требует наглядных средств обучения. Поэтому автор создал данный видеоурок.
Этот материал станет помощником каждому учителю, преподающему математику в 10 классе. Здесь содержится полезная информация, только по теме и соответствующая возрастным особенностям обучающихся.
Если учитель воспользуется данным материалом на своем уроке, то у него появится масса свободного времени, которое он до этого тратил на подготовку к уроку.
На уроке на объяснение нового материала затрачивается 5-10 минут. Данный видеоурок имеет длительность 10:11 минут, что, в общем-то, соответствует регламенту. За это время автор хорошо раскрывает тему, а обучающиеся легко смогут усвоить полученную информацию.
В самом начале урока автор отмечает, что необходимо повторить некоторые понятия, относящиеся к данной теме. В первую очередь, стоит вспомнить, какая функция называется монотонной. Определение этого понятия появляется на экране. Здесь же приводится пример конкретной функции.
Далее предлагается познакомиться с понятием обратимой функции. После определения рассматривается график некоторой функции, которую можно считать обратимой. А затем приводится пример функции, которая необратимая, так как трем разным значениям переменной xсоответствует одно и то же значение функции. Здесь же автор проговаривает, когда функция считается обратимой.
После этого предлагается рассмотреть теорему, согласно которой любая монотонная на всей области определения функция является обратимой. Эта теорема рассматривается с доказательством. В ходе доказательства автор обращает внимание слушателей к графику. При этом он ведет параллельно записи доказательства.
Когда теорема доказана, автор вводит понятие обратной функции. После того, как понятие обратной функции определено, говорится, что свойства прямой и обратной функции тесно связаны. Поэтому далее рассматриваются эти самые свойства. Последнее свойство рассматривается с подробным доказательством.
После этого на примерах показано, как находится обратная функция и ее аналитическое выражение. Примеры насыщены логическими рассуждениями, что позволяет развивать умственные способности обучающихся. Таких примеров рассмотрено три.
Далее автор вводит замечание, которое заключается в достаточности существования обратной функции, если функция монотонна. А после замечания дается алгоритм нахождения обратной функции.
На этом видеоурок заканчивается. Но учителю необходимо подобрать задания для закрепления. Данный материал будет полезен учителям и обучающимся.
ТЕКСТОВАЯ РАСШИФРОВКА:
Определение и задание обратной числовой функции.
Для изучения этой темы необходимо повторить: какая функция называется монотонной?
Функция игрек равно эф от икс называется монотонной на множестве икс большое, если она на этом промежутке или убывает или возрастает.
Пример
Функция у=eх (игрек равный е в степени икс)-возрастающая на множестве всех чисел, значит, является монотонной
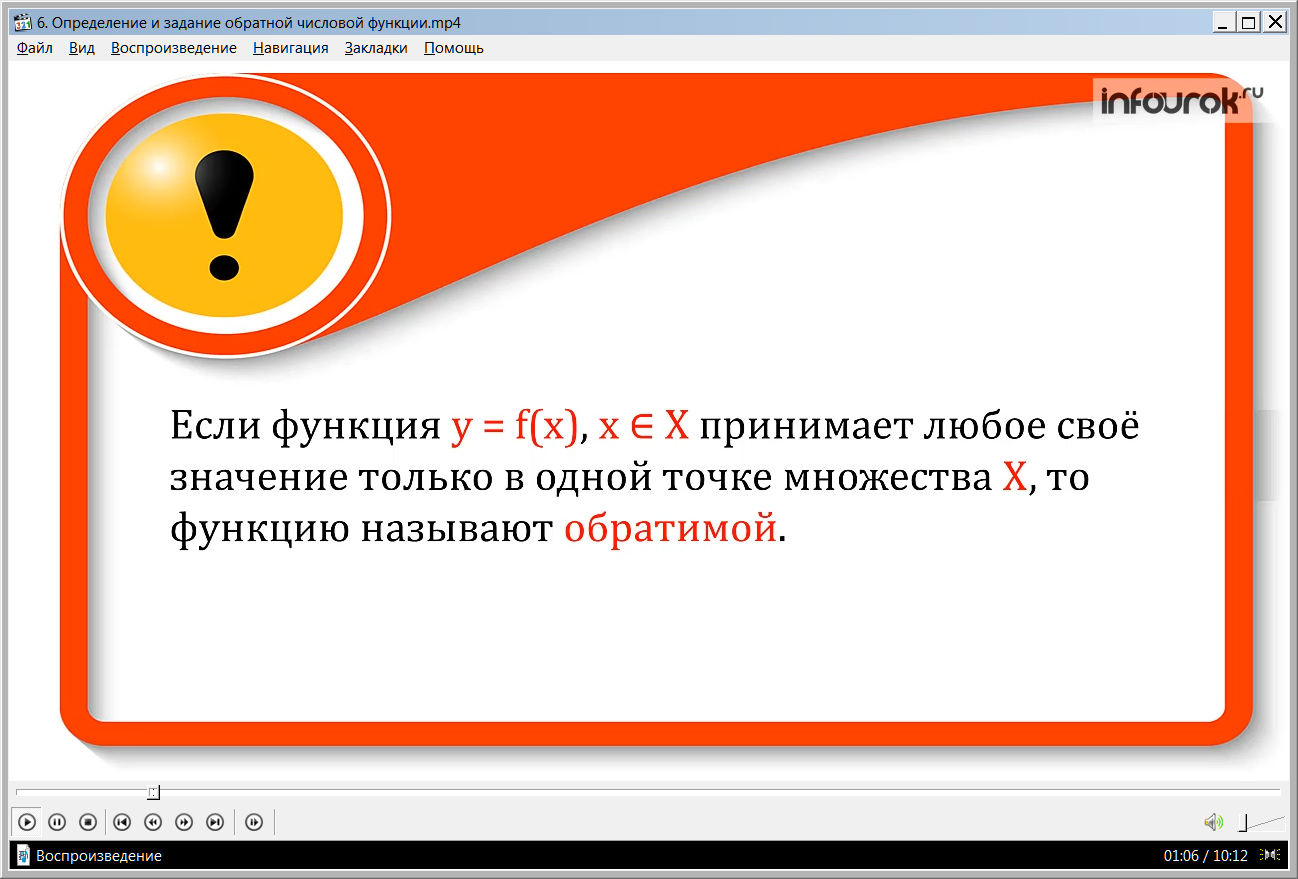
Если функция игрек равен эф от икс, где икс из множества икс большое принимает любое свое значение только в одной точке множества икс большое
( иначе говоря, если разным значениям аргумента соответствуют разные значения функции), то функцию игрек равно эф от икс, где икс из множества икс большое называют обратимой.
Рассмотрим график функции игрек равно эф от икс.
Функция игрек равен эф от икс – обратима, так как какое бы число у0 из множества значений функции , мы не взяли, оно является значением только в одной точке икс нулевое: игрек нулевой равен эф от икс нулевой.
Рассмотрим график функции игрек равен же от икс.
Сделаем вывод:
Функцию игрек равен эф от икс, где икс из множества икс большое называют обратимой, если любое свое значение она принимает только в одной точке множества икс большое.
Изучим теорему.
Если функция игрек равен эф от икс, где икс из множества икс большое монотонна на множестве икс большое,то она обратима.
Доказательство:
- Пусть функция игрек равно эф от икс возрастает на икс большое и пусть икс первое не равно икс второму- две точки множества икс большое.
- Для определенности пусть икс первое меньше икс второго.
Тогда из того, что икс первое меньше икс второго следует, что эф от икс первого меньше чем эф от икс второго. - Таким образом, разным значениям аргумента соответствуют разные значения функции, т.е. функция обратима.
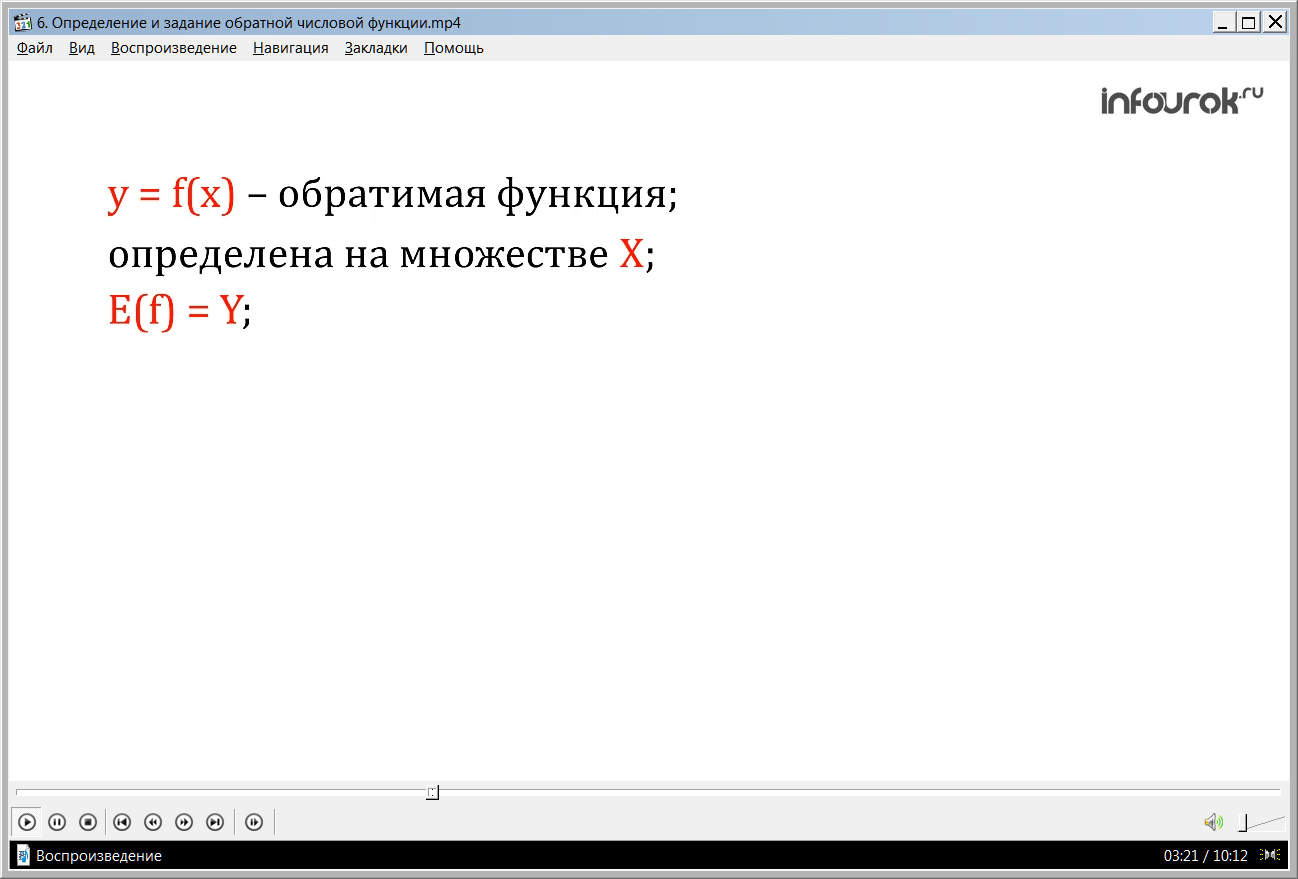
Пусть обратимая функция игрек равно эф от икс определена на множестве икс большоеи область значений есть множество игрек большое. Поставим в соответствие каждому игрек из множества игрек большое.то единственное значение икс, при котором эф от иксравно игрек. Тогда получим функцию, которая определена на множестве игрек большое, а икс большое – область значений функции.
Эту функцию обозначают икс равно эф в минус первой степени от игрек, где игрек из множества игрек большое и называют обратной по отношению к функции игрек равно эф от икс .
Свойства прямой и обратной функций, связаны между собой.
Докажем третье свойство.
Пусть игрек равно эф от икс - возрастающая функция,
игрек первое и игрек второе- значения функции, причем игрек первое меньше игрека второго.
Так как функция возрастающая, то она монотонная, а, значит, обратима.
Следовательно, каждое из этих значений достигается в одной точке:
игрек первое равно эф от икс первого и игрек второе равно эф от икс второго и икс первое меньше чем икс второе.
Предположим, что икс первое больше или равно икс второго, тогда и эф от икс первого больше или равно чем эф от икс второго , т.е. игрек первое больше или равно чем игрек второе ,так как функция игрек равно эф от икс - возрастающая .
Получили противоречие с условием. Значит, игрек первое меньше чем игрек второе. Из него следует первое меньше чем икс второе . А это означает, что обратная функция икс равно эф в минус первой степени от игрек ) возрастает на игрек большое..
Обратную функцию можно задать аналитически и графически.
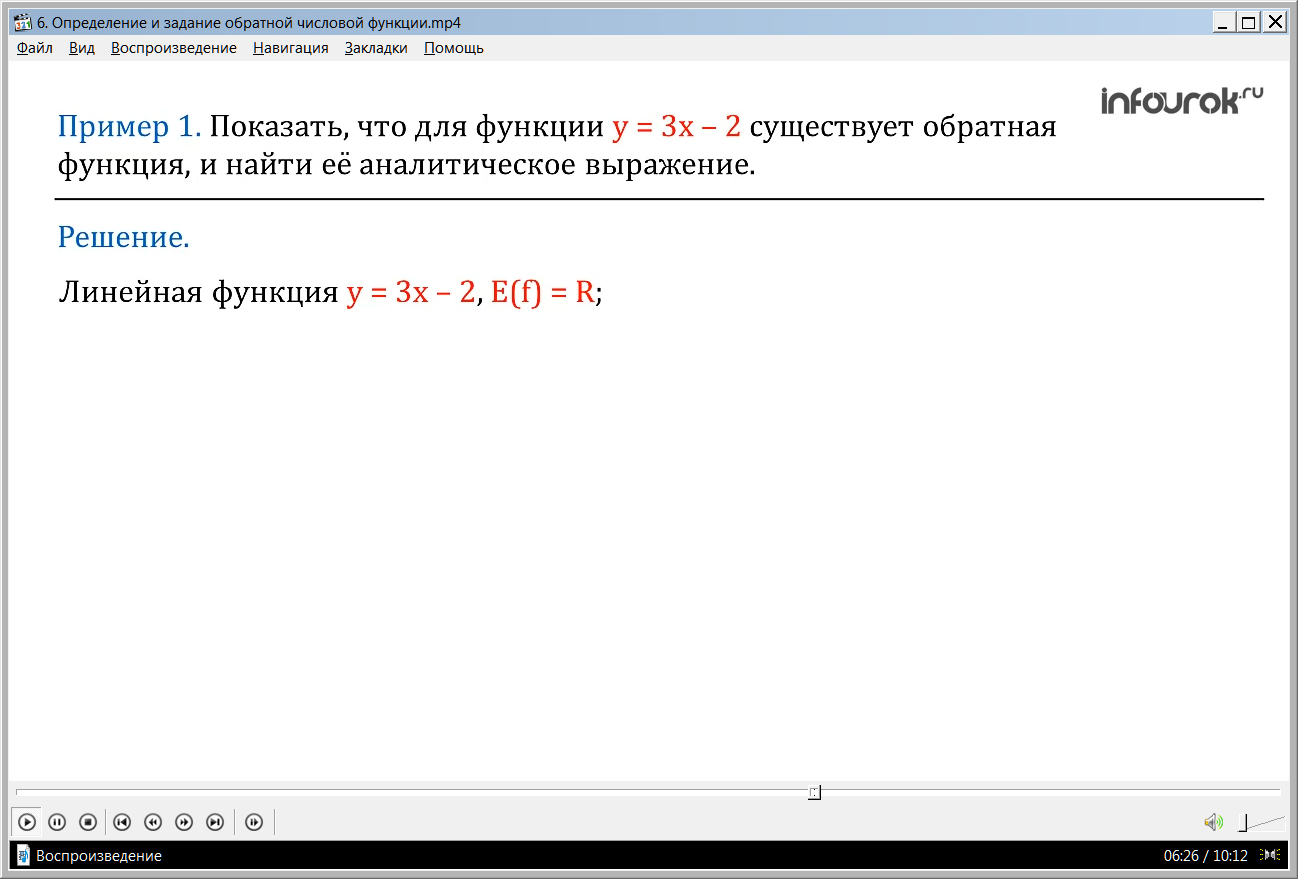
Пример 1.
Показать, что для функции игрек равно три икс минус два существует обратная функция, и найти ее аналитическое выражение.
Решение.
Линейная функция на множестве всех чисел определена на множестве всех чисел,
возрастает на множестве всех чисел
выполняется условие большему значению аргумента соответствует большее значение функции т.е. для x2>x1 соответствует y2>y1
для одного у0 существует единственный х0
и область ее значений есть множество всех чисел.
Значит, обратная функция существует на множестве всех чисел. Чтобы найти ее аналитическое выражение, решим уравнение на множестве всех чисел относительно икс; получим икс равен дроби, числитель которой равен игрек плюс два , а знаменатель равен трем. Это и есть искомая обратная функция. Она определена и возрастает на множестве всех чисел.
Не для всякой функции можно указать обратную. Условие обратимости функции - ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.
Пример 2. Найти обратную функцию к функции у=х2, на промежутке [0; )
Игрек равен икс квадрат..
Это — квадратичная функция. Область определения – множество всех чисел.
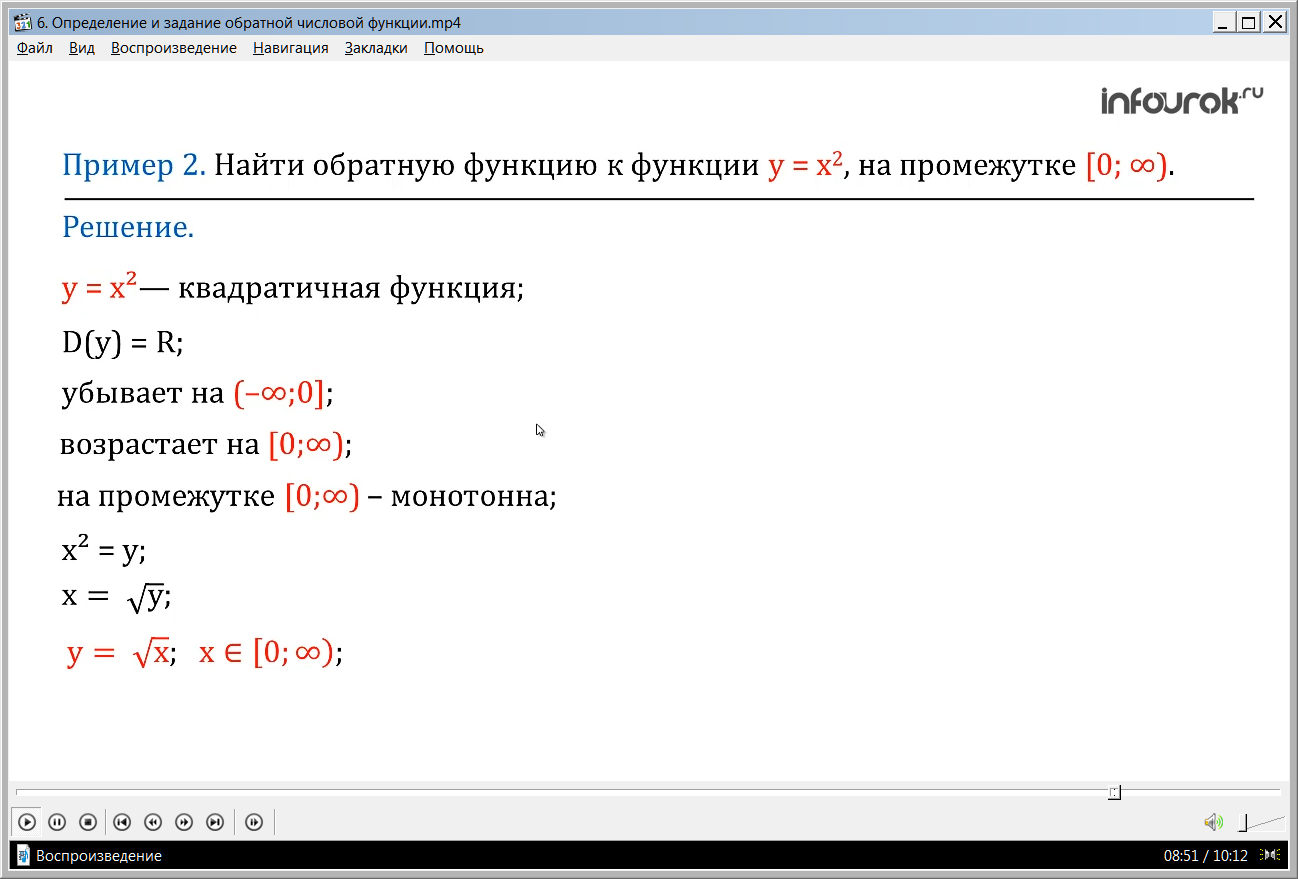
Она убывает на промежутке минус бесконечности до нуля, и
возрастает на промежутке от нуля до плюс бесконечности. На всей области определения функция не является монотонной.
На промежутке от нуля до плюс бесконечности функция монотонна, поэтому обратима. Ищем обратную функцию.
Промежутку от нуля до плюс бесконечности принадлежит только один корень икс равен квадратный корень из игрек - это и есть обратная функция на промежутке от нуля до плюс бесконечности.
Можно поменять местами икс и игрек и получим игрек равен квадратный корень из икс, где икс из промежутке от нуля до плюс бесконечности.
Пример 3.
Найти обратную функцию к функции игрек равно икс в кубе.
Решение:
Дэ от игрек равно эр большое ,функция монотонна на всей области определения, тогда существует обратная функция.
Решаем:
Получим игрек равен кубический корень из икс – обратная функция.
Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием
Из выше изложенного материала можно составить алгоритм нахождения обратной функции:
1) Убедиться, что функция монотонна.
2) Выразить переменную х через у.
3) Переобозначить переменные. Вместо икс равен эф в минус первой степени от игрек пишут игрек равен эф в минус первой степени от икс.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4474 |
| Номер материала | 829 |