
Урок "Определение производной"

Краткое описание документа:
Видеоурок «Определение производной» предназначен для наглядного представления учебного материала по данной теме. Основываясь на изученном материале о пределе функции, понятии приращения аргумента и функции, раскрывается понятие производной функции. Представлены соответствующие определения, рассматриваются примеры, помогающие усвоить тему и научиться применять полученные знания при решении задач.
Видеоурок начинается с представления темы урока и введения понятия производной функции, которое возникает в процессе построения математической модели при решении задачи о скорости движения по физике. Описывается условие задачи, в которой дано перемещение тела на некоторое расстояние. При этом закон движения описан функцией s=s(t). Перемещение описано с помощью координат на плоскости. Необходимо найти скорость движения в некоторый момент t. Построение математической модели начинается с начала отсчета, в котором перемещение тела в определенный момент времени вычисляется на координатной плоскости отрезком OL=s(t). Через некоторый промежуток времени t+Δt перемещение определяется значением функции от приращенного аргумента ОК= s(t+Δt). При этом пройденный путь тела определяется разностью LК=ОК- OL= s(t+Δt)- s(t), где LК=Δs – изменение положения тела. Зная зависимость перемещения тела от скорости, за некоторый промежуток времени [t,t+Δt] тело движется со средней скоростью vср.= Δs/Δt. Мгновенная скорость принимает значение, которое определяется наименьшим промежутком времени изменения положения тела, то есть vt=lim vср. при Δt→0.
Следующий пример рассматривает приложение понятия производной при решении геометрических задач. Для этого сначала раскрывается понятие касательной. На координатной плоскости изображается график функции, на котором отмечаются две точки M и S. Через отмеченные точки проводится прямая. Демонстрируется, как при приближении точки S к точке М положение соединяющей точки прямой приближается к положению касательной в точке М. То есть касательная представляет собой предельное положение секущей, соединяющей две точки графика при сближении точек. После введения понятия касательной рассматривается касательная к графику функции y=f(x) в точке М(а, f(a)). Необходимо найти угловой коэффициент касательной. Для этого на некотором расстоянии от М отмечается точка N(а+Δх, f(a+Δх)). Угловой коэффициент прямой представляет тангенс угла, под которым лежит прямая, содержащая гипотенузу треугольника, образованного приращением аргумента Δх и приращением функции Δу. Соответственно, угловой коэффициент секущей находится по формуле kсек.= Δу/Δх. При приближении точек Δх→0. Очевидно, что коэффициент касательной при сближении точек определяется предельным положением секущей при Δх→0, kкас.= lim kсек. или kкас.= lim Δу/Δх.
Выводы из особенностей математической модели решения обеих задач оформляются в виде определения производной функции, нахождение которой фигурирует в задачах. Отмечается, что для функции y=f(x), определенной в точке х и ее окрестности, предел Δу/Δх при Δх→0 называется производной y=f(x) в этой точке. Вводится обозначение производной f′(x). Для усвоения материала рассматривается производная линейной функции – отмечается, что так как найденный ранее для функции y=kx+m предел lim Δу/Δх=k при Δх→0, то y′=(kx+m)′= k. Также, найденный предел функции y=x3, равный lim Δу/Δх=3х2 при Δх→0 означает, что производная y′=(x3)′= 3х2.
Раскрывается физический и геометрический смысл производной. Отмечено, что в физическом смысле для закона прямолинейного движения s(t) производная означает мгновенную скорость v= s′(t). В геометрическом смысле для касательной , проведенной в точке х=а к графику функции y=f(x) производная f′(а) – угловой коэффициент касательной.
Рассматривая смысл производной и формулу для ее нахождения lim Δу/Δх= f′(х) при Δх→0, отмечается почти прямая пропорциональность приращения функции от приращения аргумента с коэффициентом, представляющим собой производную Δу≈f′(х)·Δх. Таким образом, для производной функции y=x3 верно соотношение Δу≈3х2·Δх.
Дается алгоритм нахождения производной функции, в котором требуется:
- В точке х найти f(x);
- При переходе в точку х+Δх найти f(х+Δх);
- Найти приращение функции f(х+Δх)- f(x);
- Составить отношение Δу/Δх;
- Найти lim Δу/Δх при Δх→0, то есть f′(х).
Согласно данному алгоритму, демонстрируются примеры определения производной функций f(x)=С, где (С)′=0; f(x)=1/х, где (1/х)′=-1/х2.
Раскрывается понятие дифференцирования функции, то есть нахождения ее производной. Отмечается, что функция является дифференцируемой в точке, если она имеет в ней производную, а также дифференцируемость функции в точке означает непрерывность функции в ней, при этом обратное утверждение неверно. Подтверждающим примером данному утверждению является нахождение производной в точке х=0 функции у=|x|. Отмечается, что несмотря на непрерывность функции в этой точке, касательной к графику в ней не может быть. А значит, и нет в этой точке производной. Данный вывод отображен на экране отдельно и рекомендован для запоминания. Примером утверждения служит функция y=f(x), которая на х<0 равна -√-х, а на промежутке x>=0 равна √х. На рисунке построен график функции, на котором хорошо видна непрерывность функции. Однако в точке х=0 касательную к графику построить нельзя, поэтому в этой точке нет производной. Напоминается, что если в некоторой точке графика функции касательную построить нельзя, или она перпендикулярна оси абсцисс, функция недифференцируема. В данном примере функция недифференцируема. На произвольном графике функции в последнем примере рассматривается ее дифференцируемость в трех точках.

Видеоурок «Определение производной» рекомендуется применять на традиционном уроке алгебры для наглядности или с целью освободить учебное время для улучшения индивидуальной работы учителя с учениками. Ученикам, слабо освоившим тему, материал может быть рекомендован для самостоятельной работы.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим две различные задачи, физическую и геометрическую, которые как приведут к возникновению новой математической модели.
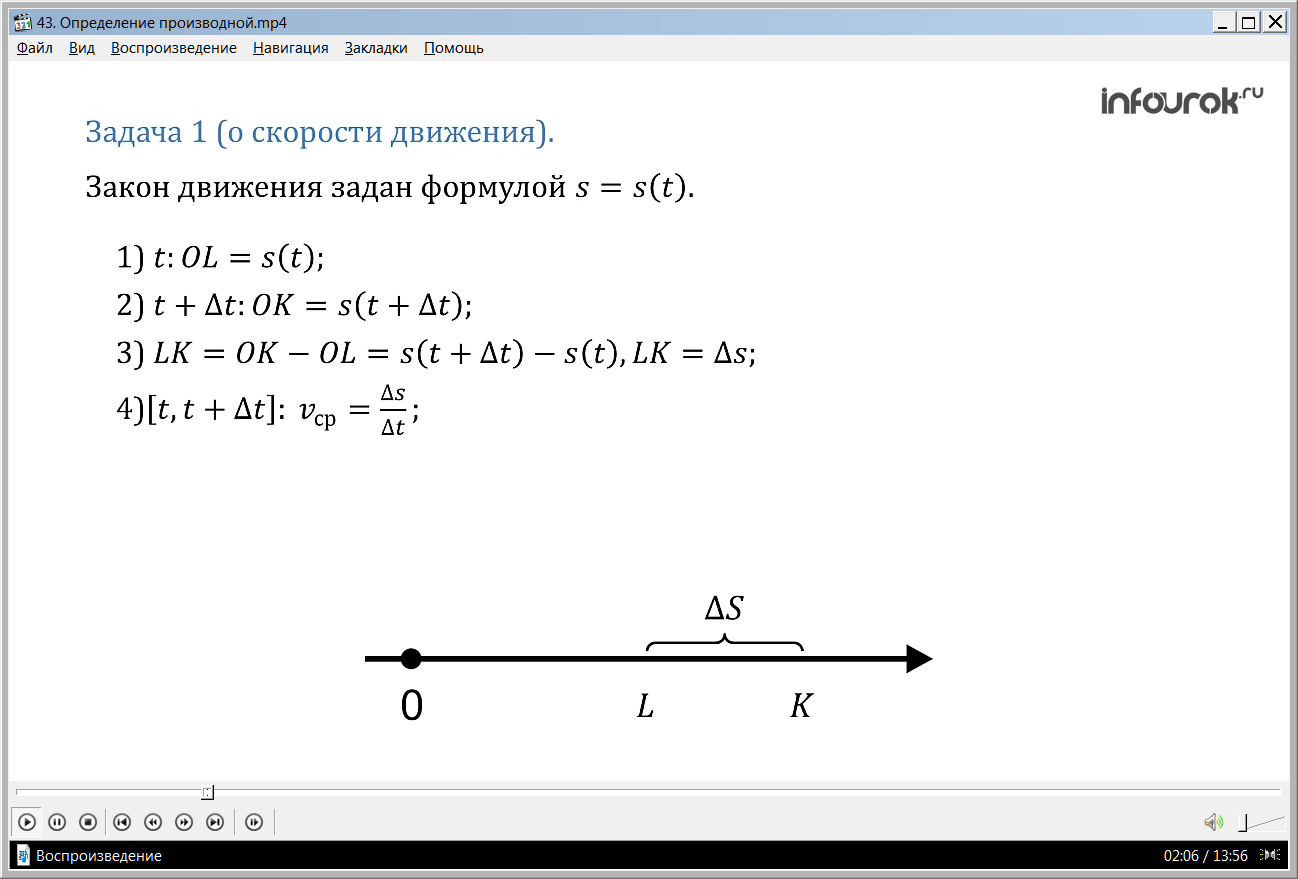
Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s (t) (эс равное эс от тэ), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).
Решение. Предположим, что в момент времени t тело находилось в точке
L (рис. 1), пройдя путь от начала движения ОL = s(t). Дадим аргументу t
приращение Δt(дельта тэ) и рассмотрим момент времени t + Δt. Координата материальной точки стала другой, тело в этот момент будет находиться в точке K: OK = s(t + t) (о ка равно эс от тэ плюс дельта тэ) .
Значит, за t секунд тело переместилось из точки L в точку K, т.е. прошло путь LK. Имеем: LK=ОK–ОL = s(t + t)–s(t). Полученную разность мы назвали приращением функции: s(t+t)–s(t) = s. Итак, LK = s(метров).
Путь s (метров) тело прошло за t секунд. Нетрудно найти среднюю скорость движения тела за промежуток времени [t, t + t]: vср. = (м/с) (средняя скорость равна отношению дельта эс к дельта тэ).
А что такое скорость v(t) в момент времени t (ее называют иногда мгновенной скоростью). Можно сказать так: это средняя скорость движения за промежуток времени [t, t + t] при условии, что t выбирается все меньше и меньше; иными словами, при условии, что t0. Это значит, что
v(t) = (вэ от тэ равно пределу средней скорости ) и
Подводя итог решению задачи 1, получаем:
Для решения следующей задачи нам нужно выяснить, что следует понимать под касательной к кривой.
Дана кривая L (рис. 2), на ней выбрана точка М. Возьмем еще одну точку на кривой, причем достаточно близкую к М, — точку S.
Проведем секущую МS. Далее будем приближать точку S по кривой L к
точке М. Секущая МS будет изменять свое положение, она как бы поворачивается вокруг точки М. Часто бывает так, что можно обнаружить в этом процессе прямую, представляющую собой некое предельное положение секущей; эту прямую — предельное положение секущей — называют
касательной к кривой L в точке М.
Задача 2 (о касательной к графику функции). Дан график функции y = f(x). На нем выбрана точка М(а; f(a)) (эм с координатами а и эф от а), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует).
Найти угловой коэффициент касательной.
Решение. Дадим аргументу приращение х и рассмотрим на графике (рис. 3) точку N с абсциссой а + х. Ордината точки N равна f(a + x) . Угловой коэффициент секущей МN, т.е. тангенс угла между секущей и осью х, вычисляется по формуле (ка секущей равен дельта игрек, деленное на дельта икс).
Если мы теперь устремим х к нулю, то точка N начнет приближаться по кривой к точке М. Касательную мы характеризовали
как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной kкac будет вычисляться по формуле (ка касательной равно пределу ка секущей).
Используя приведенную выше формулу для kсек, получаем: ( ка касательной равно предел дельта игрек, деленное на дельта икс, при стремлении дельта икс к нулю).
Подведем итоги. В процессе решения двух задач мы пришли к одной и той же математической модели — пределу отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Рассмотрим, что из себя представляет предел отношения приращения функции к приращению аргумента.
2. Определение производной
Определение 1. Пусть функция у =f(x) определена в конкретной точке х и в некоторой ее окрестности. Дадим аргументу х приращение х, такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функции Δу и составим отношение . Если существует предел этого отношения при условии х0, то указанный предел называют производной функции у = f(х) в точке х и обозначают f'(x)(эф штрих от икс).
Итак, (предел дельта игрек, деленное на дельта икс, равен эф штрих от икс).
Для обозначения производной часто используют символ у'. (игрек штрих)
Отметим, что у'=f'(x) (игрек штрих равен эф штрих от икс)— это новая функция, но, связанная с функцией y = f(x), определенная во всех таких точках х, в которых существует указанный выше предел. Эту функцию называют так: производная функции у =f(x).
В примере для линейной функции y=kx + m справедливо равенство: .
Это означает, что y'=k или, подробнее,
(kx + m)' =k. (производная ка икс плюс эм равна ка).
В частности,
(х)'=1.
Мы доказали, что для функции у = х3 справедливо равенство
Это означает, что у'=3х2 или, подробнее, (x3)' = 3х2.(икс в кубе штрих равно три икс во второй степени)
Производная с физической и геометрической точек зрения.
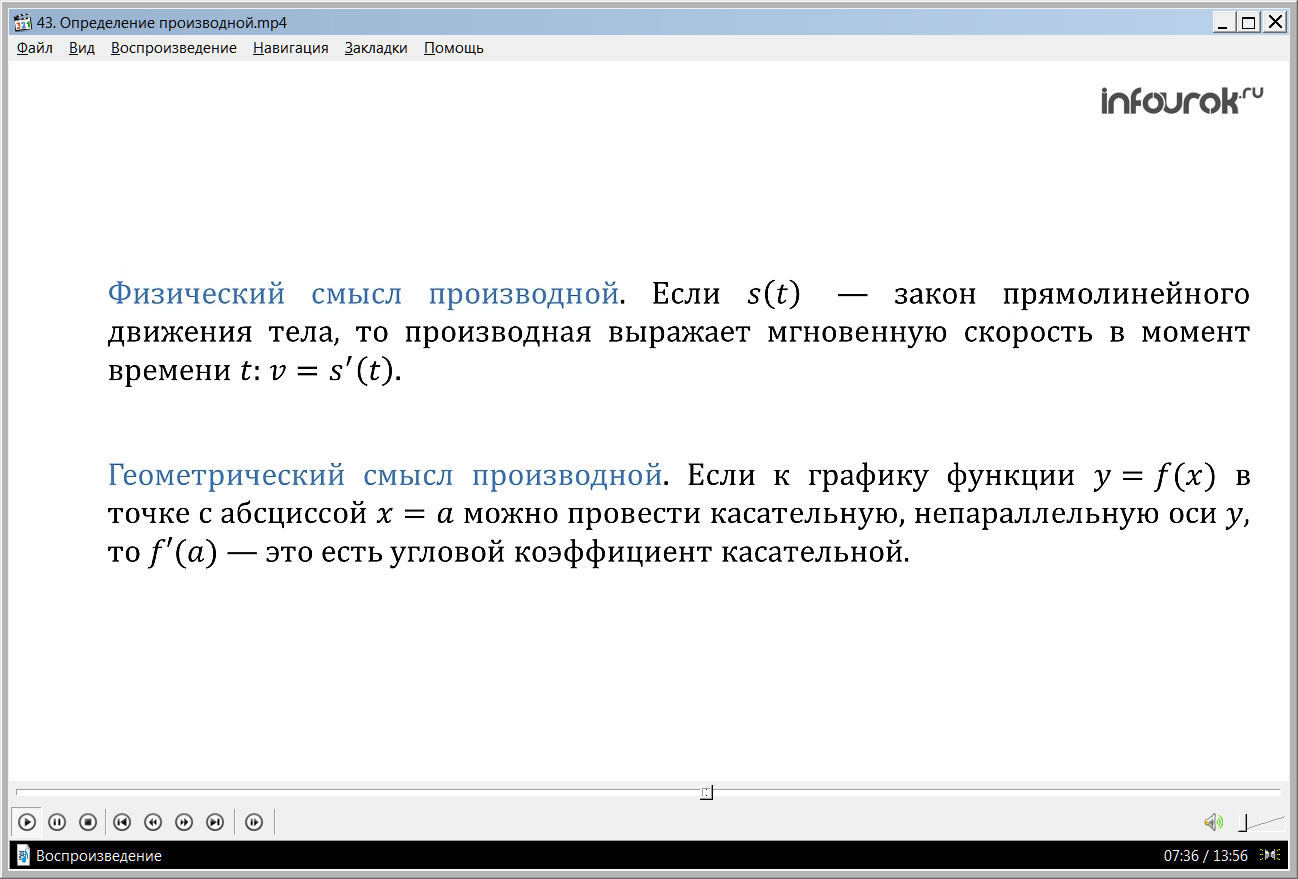
Физический (механический) смысл производной состоит в следующем. Если s (t) — закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t:
v=s´(t) (вэ равно эс штрих от тэ).
Геометрический смысл производной состоит в следующем. Если к графику функции y= f(x) в точке с абсциссой х=а можно провести касательную, непараллельную оси у, то f'(a) –это есть угловой коэффициент касательной .
Пусть функция у = f(x) имеет производную в конкретной точке х: (предел отношения приращения функции к приращению аргумента равен производной функции).
Получаем: в достаточно малой окрестности точки х выполняется приближенное равенство: (отношения приращения функции к приращению аргумента приближённо равно производной функции) или
y f'(x) ·х. (приращения функции приближённо равно производной функции, умноженной на приращение аргумента).
Приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной (в заданной точке х). Например, для функции у = х3 справедливо приближенное равенство y 3х2 ·х
Сформулируем алгоритм отыскания производной.
АЛГОРИТМ ОТЫСКАНИЯ ПРОИЗВОДНОЙ (для функции у = f(x))
1. Зафиксировать значение х, найти f(x).
2. Дать аргументу х приращение х, перейти в новую точку
х + х, найти f(x + x).
3. Найти приращение функции: y= f(x + x)–f(x).
4. Составить отношение .
5. Вычислить предел .
Этот предел и есть f'(x).
Пример 1. Найти производную постоянной функции у = С.
Решение. Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х имеем: f (х) = С.
2) В точке х + х имеем: f(x + х)=С.
3) у=С–С=0.
4) ==0
5) ==0.
Ответ: (С)'=0.
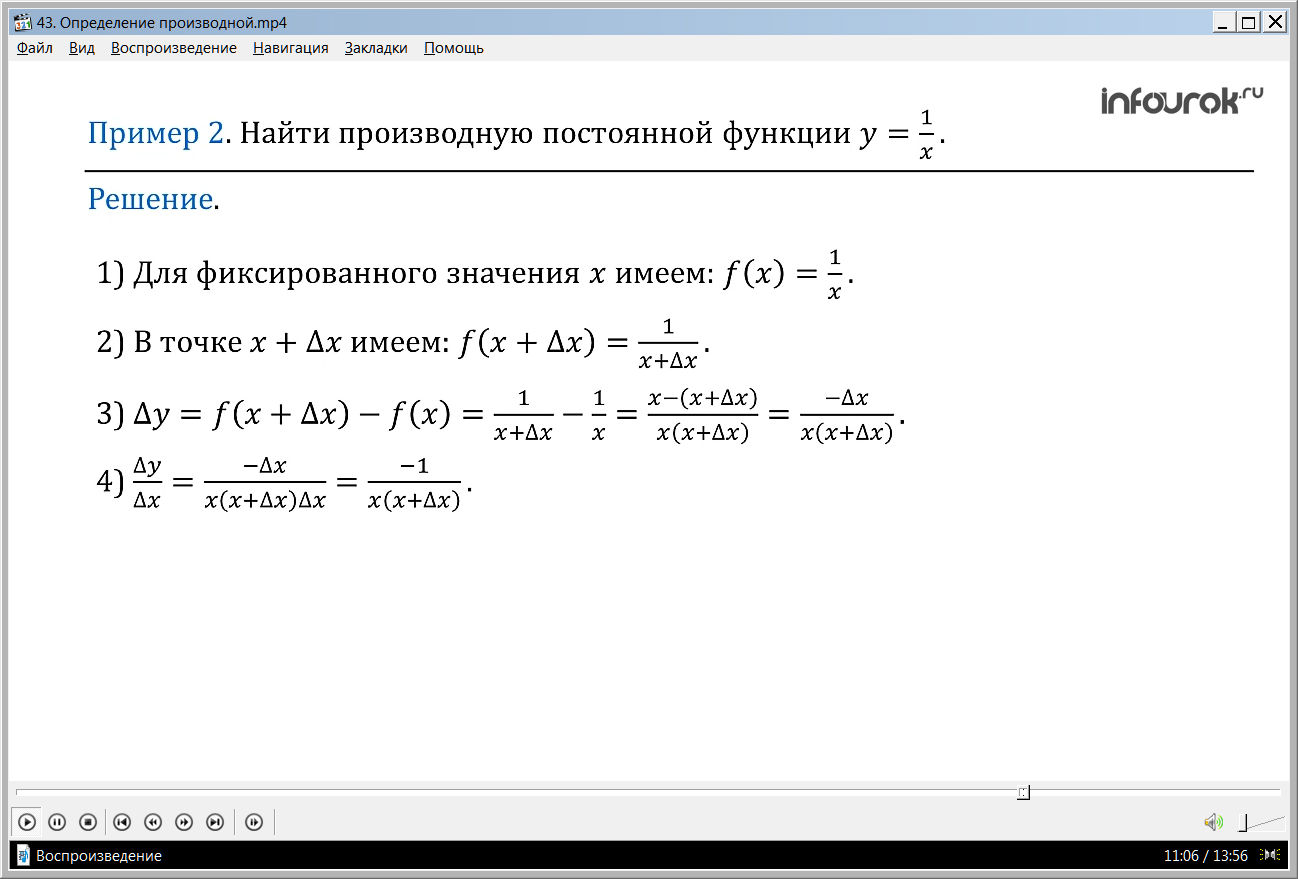
Пример 2. Найти производную функции у = .
Решение. Воспользуемся алгоритмом отыскания производной.
Если функция y = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Нахождение производной функции y = f(x) называется дифференцированием функции y = f(x).
Если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное же утверждение неверно.
Приведем примеры: функция y=|х| непрерывна везде, и в точке х =0 (рис. 4), но касательной к графику функции в «точке стыка» (0; 0) не существует.
Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производной.
Пример. На рис. 5 изображен график кусочной функции y=f(x), где
Функция непрерывна на всей числовой прямой, в том числе в точке х=0. И касательная к графику функции существует в любой точке, в том числе в точке х=0. Но в точке х=0 касательная совпадает с осью у, т.е. перпендикулярна оси абсцисс, ее уравнение имеет вид х=0.Такая прямая не имеет углового коэффициента, поэтому, не существует и f'(0).
Чтобы по графику сделать вывод о дифференцируемости функции, необходимо проверить, можно ли в некоторой точке провести касательную к графику функции, не перпендикулярную оси абсцисс. Если можно, тогда в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция недифференцируема. Так, по графику функции, изображенному на рис. 6, можно сделать вывод: функция непрерывна всюду, кроме точки х =а; функция дифференцируема всюду, кроме точек х=а, х=b – здесь касательная не существует, х=с –здесь касательная параллельна оси у.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9890 |
| Номер материала | 866 |