
Урок "Отображение плоскости на себя"

Краткое описание документа:
Видеоурок «Отображение плоскости на себя» является наглядным пособием для представления на уроке геометрии данной темы. Тема отображение плоскости на себя является важной для формирования понятия учеников о плоскости и подведения к понятию движения. Глубокое понимание предмета изучения дает возможность освоить дальнейший курс геометрии, связанный с общим представлением операцийна плоскости. Задача наглядного пособия – представить учебный материал в форме, наиболее эффективной для усвоения учениками. Материал может применяться, сопровождая объяснение учителя. Также данный материал может заменить объяснение учителя, освобождая его для решения других учебных задач.
Сформировать понимание материала помогают анимационные эффекты, выделение цветом, голосовые комментарии. Благодаря кадрированию материала и анимации, учебный материал подается последовательно, хорошо структурирован, давая возможность ученику постепенно и с глубоким пониманием освоить сложные понятия. Важные выводы, формулировки и рисунки окрашены в различные цвета. При помощи цвета выделены важные детали построения, понятия. Это способствует запоминанию материала, формированию глубоких знаний.
Видеоурок начинается с демонстрации названия темы. Ученикам предлагается представить ситуацию, когда производится сопоставление любой точке некоторой плоскости определенной точки этой же плоскости, при этом все точки плоскости имеют сопоставление в некоторой точке. Таким образом формируется понятие отображения плоскости на себя. Для усвоения данного понятия приводится пример, уже изученный учениками в курсе математики – понятие симметрии. На экране демонстрируется ось а, относительно которой выполняется симметрия, строится некоторая точка М с одной стороны оси. Отмечается, что для построения симметричной точки М1 относительно имеющейся прямой а необходимо провести от нее перпендикуляр к прямой а.

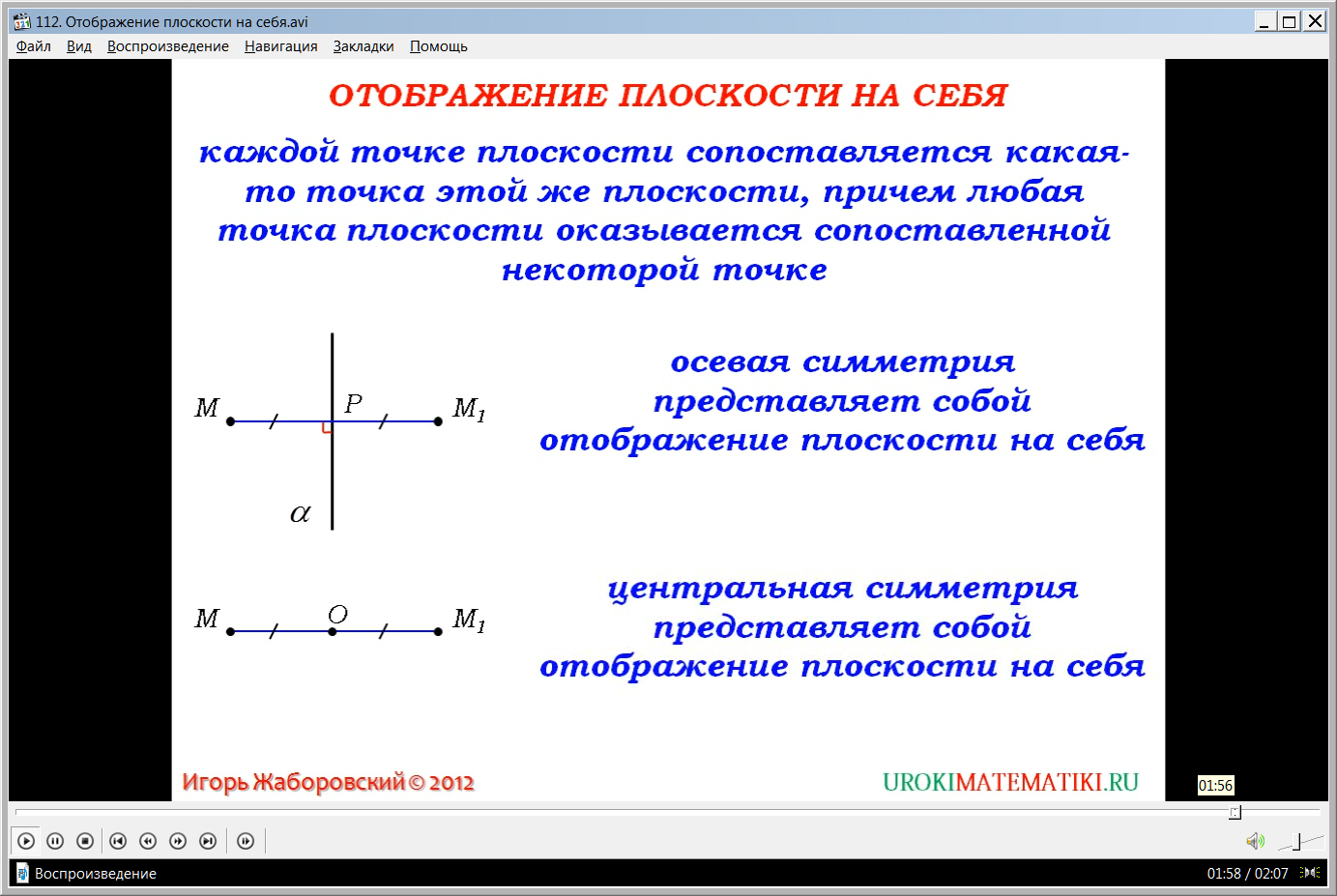
После построения прямой МР, перпендикулярной к оси симметрии а, на продолжении прямой откладывается отрезок РМ1, равный отрезку МР, при помощи которого и формируется точка, симметричная точке М.Также отмечается, что для точки, принадлежащей прямой а, построенная симметричная точка совпадет с имеющейся М. Из сделанного построения делается общий вывод – при построении симметрии каждой точке на плоскости сопоставляется также некоторая точка плоскости и всякая точка М1 будет сопоставлена некоторой М. Таким образом, рассмотренное понятие осевой симметрии является отображением плоскости на себя. Этот вывод выведен на экран и рекомендован к запоминанию.

Аналогично анализу осевой симметрии рассматривается понятие симметрии относительно точки. Для проведения анализа на экране демонстрируется построение соответствующей симметрии. Выбирается некоторая точка О, которая является центром симметрии и отмечается точка М. К центру симметрии проводится отрезок, соединяющий его с М. На продолжении прямой, на которой лежат точки М и О, от точки О откладывается отрезок, длина которого равна длине ОМ. На конце построенного отрезка отмечается точка М1, которая является симметричной М относительно центра симметрии О. Делается вывод о том, что центральная симметрия также, как и осевая, является отображением плоскости на себя. Ученикам рекомендуется самостоятельно обосновать данный вывод на основе сделанного построения.
Видеоурок «Отображение плоскости на себя» может применяться для повышения эффективности традиционного урока геометрии в школе. Также наглядное пособие необходимо учителю, осуществляющему дистанционное обучение. Пособие можно рекомендовать ученикам, которые самостоятельно осваивают предмет или требуют дополнительного материала для освоения темы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4414 |
| Номер материала | 747 |