
Урок "Параллелепипед"

Краткое описание документа:
Видеоурок «Параллелепипед» описывает виды и свойства параллелепипеда. В ходе демонстрации доказывается важная теорема, знание которой помогает решить практические задачи, связанные с параллелепипедом. Задача видеоурока – сформировать представление о свойствах параллелепипеда со стороны стереометрии. Материал может быть использован как наглядное пособие при ведении школьного урока математики, а также стать самостоятельной частью урока. С помощью видеоурока можно повысить эффективность урока геометрии, обеспечить лучшее решение учебных целей и задач.
Форма видеоурока имеет множество преимуществ, определенных возможностями видео. При составлении материала используются анимационные эффекты, «оживляющие» картинку, а также обеспечивающие логичную последовательную подачу материала. При помощи специальных выделений акцентируется внимание на определениях и формулировках, важных деталях построений. Благодаря этому обеспечивается лучшее запоминание материала, более глубокое его понимание.

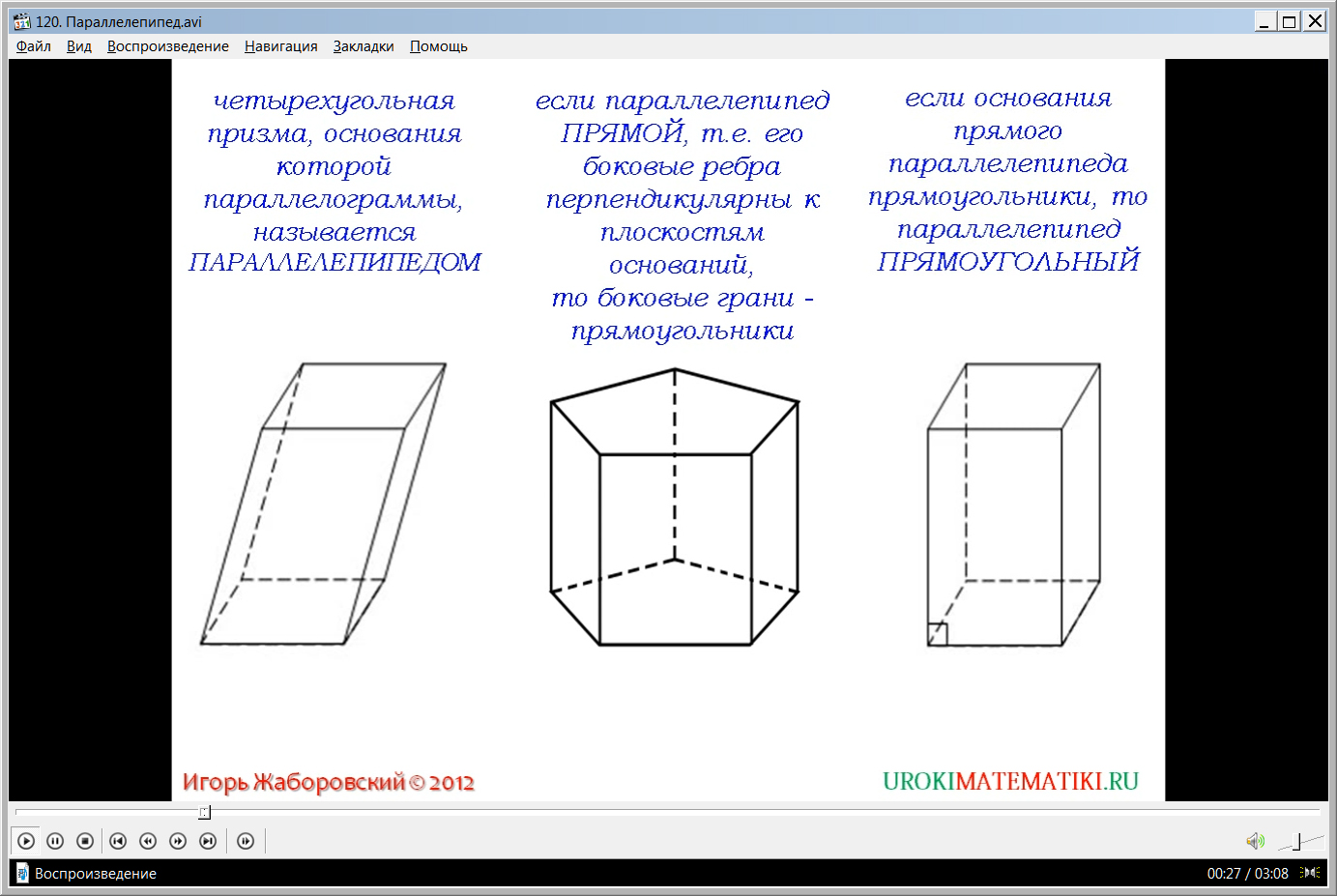
Видеоурок начинается с представления его названия и определения параллелепипеда. Ученикам напоминается, что параллелепипед – это четырехугольная призма, в основании которой лежат параллелограммы. Отмечается, что все шесть граней параллелепипеда являются параллелограммами. Если угол между боковыми гранями и плоскостями основаниями прямой, то есть параллелепипед прямой, то боковые грани являются прямоугольниками. В случае, когда в прямом параллелепипеде основания также являются прямоугольниками, то параллелепипед является прямоугольным.
Далее рассматривается свойство диагоналей параллелепипеда, аналогичное свойству диагоналей параллелограмма. Ученикам напоминается, что диагонали параллелограмма точкой пересечения делятся на равные части. Аналогично диагонали параллелепипеда (все четыре), точкой пересечения, одной для всех четырех, делятся также пополам. Описывается доказательство данного утверждения.

Доказательство утверждения начинается с теоремы о том, что при параллельности двух прямых третьей, они являются параллельными между собой. Отмечается, что подобное утверждение было доказано в планиметрии относительно расположения прямых на плоскости. Также оно верно и для расположения прямых в пространстве. К доказательству на экран выводится рисунок, на котором изображен параллелепипед ABCDA1B1C1D1. Отмечается, что основаниями данного параллелепипеда служат параллелограммы ABCD и A1B1C1D1. Из данных параллелограммов следует справедливость утверждений о том, что BC параллельна AD и они равны между собой, также A1D1 параллельна AD, и они также являются равными. Изданных равенств следует и равенство и параллельность противолежащих сторон параллелограммов BC= A1D1. Из рассмотренных свойств следует, что фигура A1D1BC также является параллелограммом. Диагонали же данного параллелограмма являются и диагоналями параллелепипеда. По известному свойству диагоналей параллелепипеда, они точкой пересечения делятся пополам. Аналогично данному ходу рассуждений доказывается, что фигура, образованная в результате соединения вершин ABC1D1 также является параллелограммом.
Точка пересечения диагоналей делит их пополам. Эти же диагонали параллелограмма являются диагоналями параллелепипеда. Таким же образом доказывается подобное свойство относительно диагоналей из параллелограмма A1B1CD. Теорема доказана.

Видеоурок «Параллелепипед» применяется для повышения эффективности школьного урока геометрии. Также материал может применяться для наглядности представления материала в ходе дистанционного обучения. Видеоурок может рекомендоваться ученикам для самостоятельного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 3139 |
| Номер материала | 740 |