
Урок «Переход к новому основанию логарифма»

Краткое описание документа:
Рассмотрим примеры логарифмических уравнений.
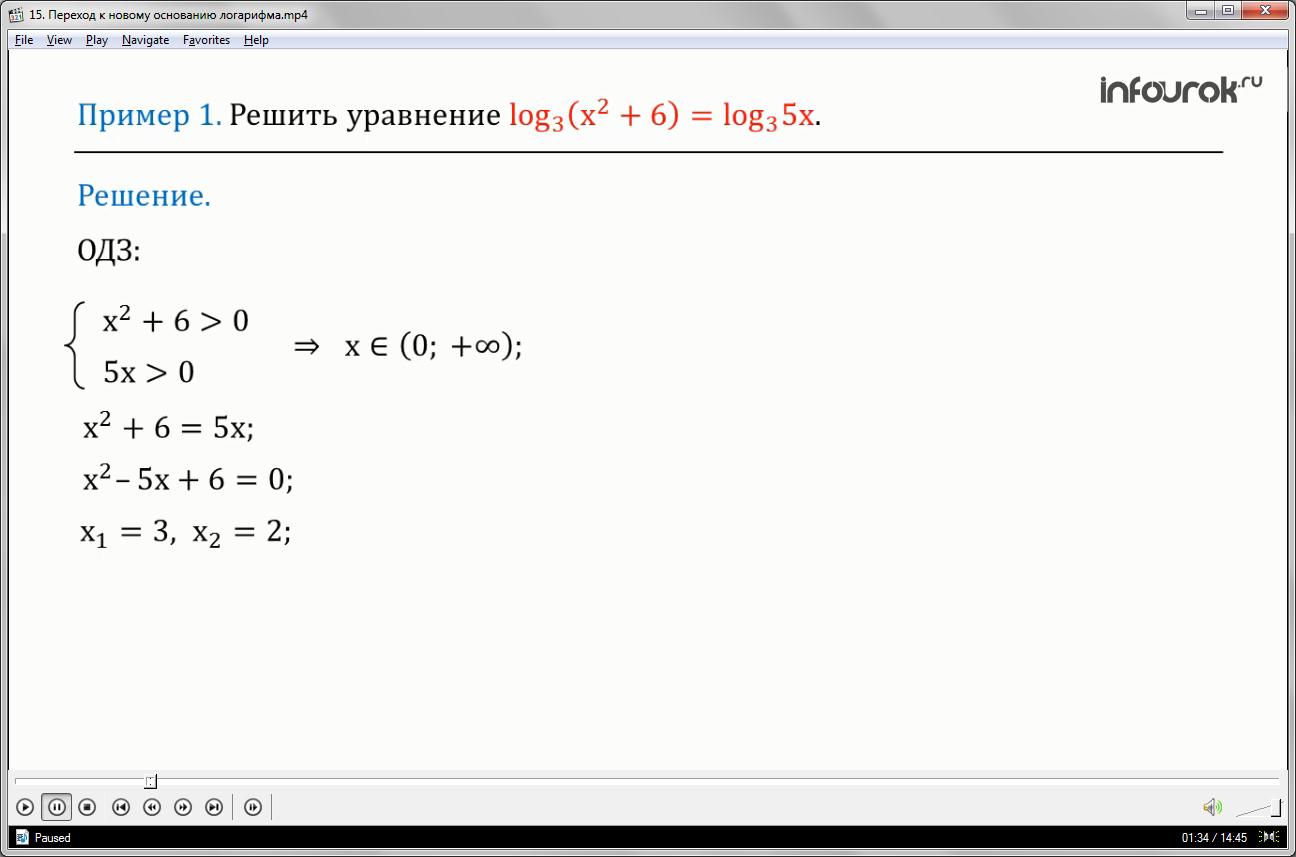
Пример 1. Решить уравнение
Для решения используем способ потенцирования. Неравенства >0 и >0 будут определять область допустимых значений уравнения. Неравенство >0 справедливо при любых значениях х, так как а 5х>0 только при положительных значения х. Значит ОДЗ уравнения — множество чисел от нуля до плюс бесконечности. Уравнение равносильно квадратному уравнению . Корни этого уравнения — числа 2 и 3,так как произведение этих чисел равно 6, а сума этих чисел равна 5 –противоположному значению коэффициента b? Оба этих числа лежат в промежутке, значит, они и есть корни этого уравнения. Заметим, что мы с лёгкостью решили данное уравнение.
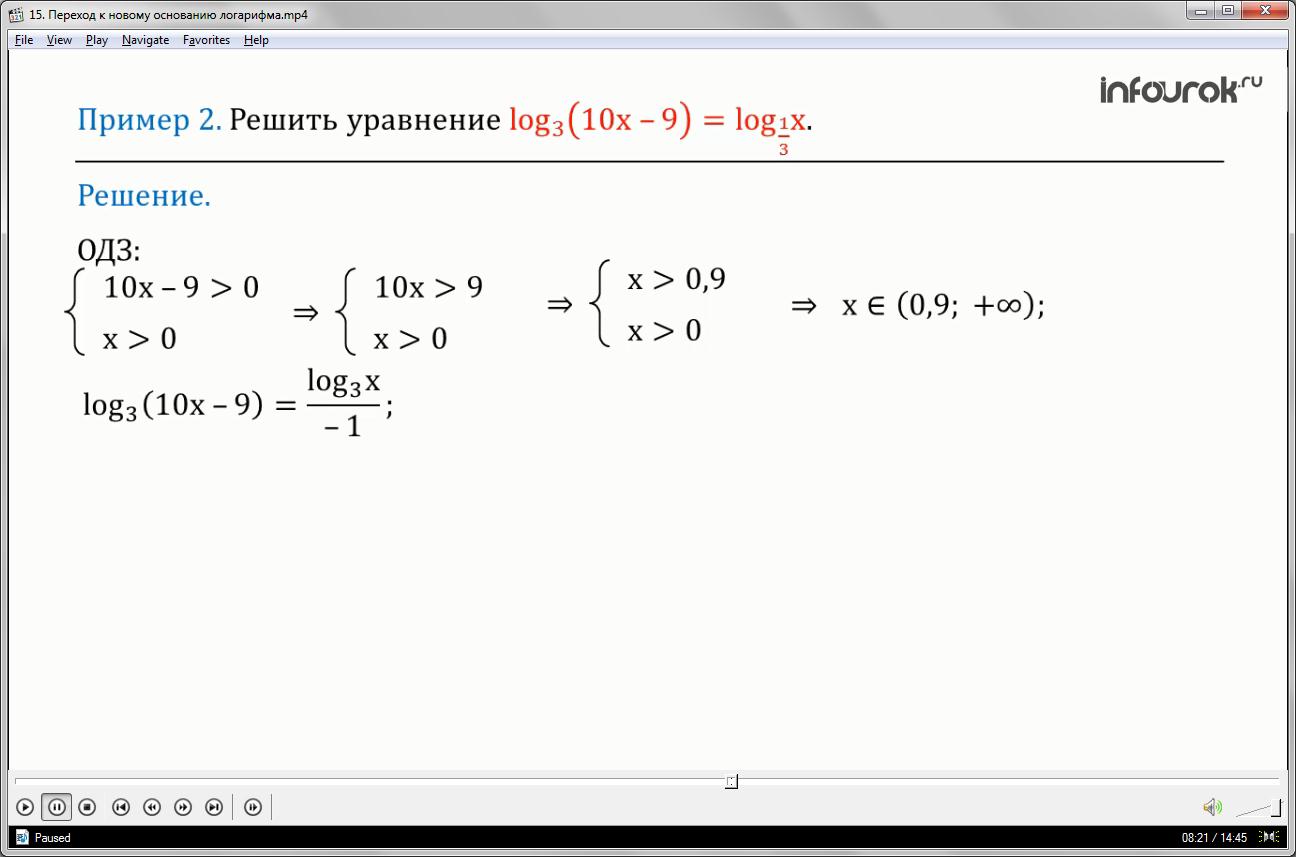
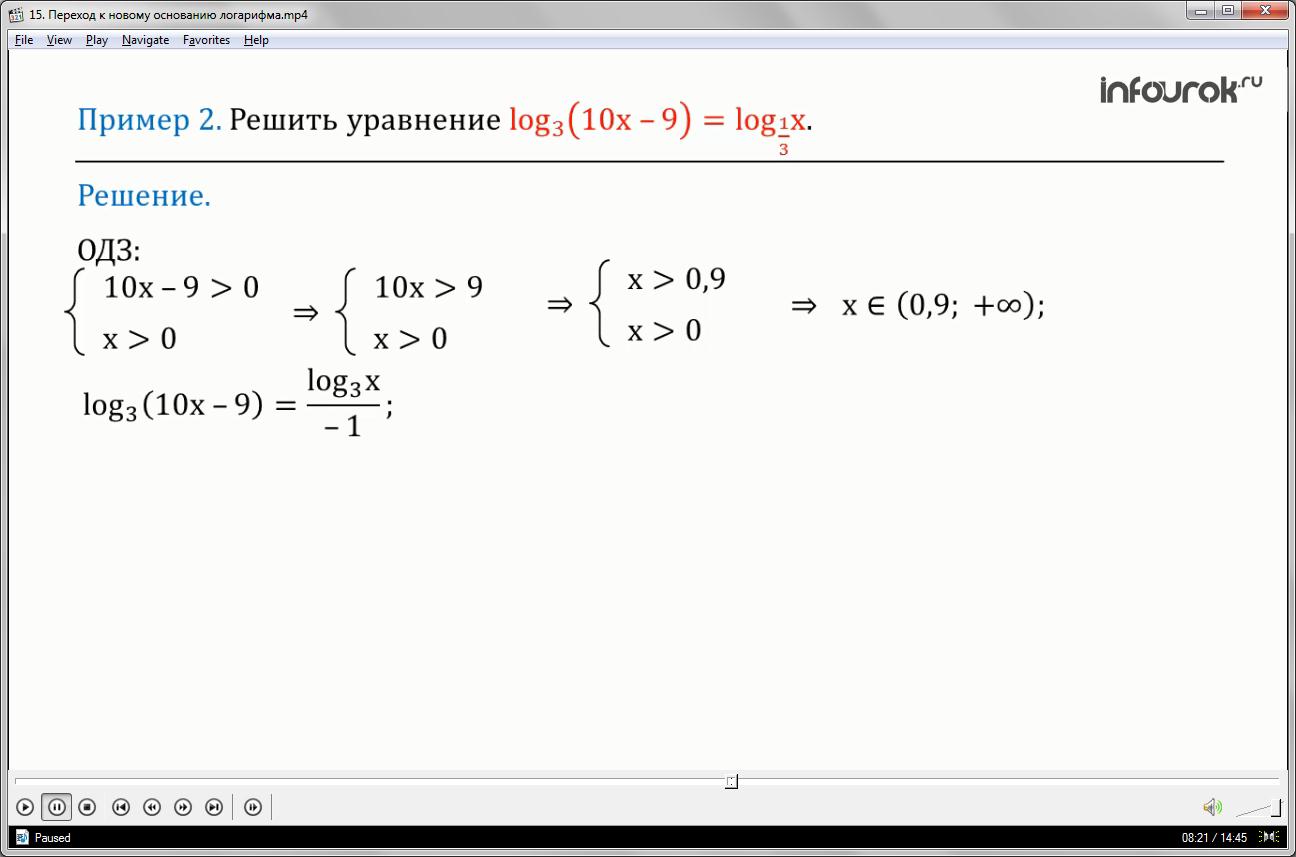
Пример 2. Решить уравнение
(логарифм выражения десять икс минус девять по основанию три равен логарифму икс по основанию одна третья)
Это уравнение отличается от предыдущего тем, что логарифмы имеют разные основания. И рассмотренный метод решения уравнения здесь использовать уже нельзя, хотя можно найти область допустимых значений и попробовать решить уравнение функционально графическим методом. Неравенства >0 и x>0определяют область допустимых значений уравнения, значит . Рассмотрим графическую иллюстрацию этого уравнения. Для этого построим по точкам график функции и . Мы можем утверждать, только что у данного уравнения есть единственный корень, он положительный, лежит на интервале от 1 до 2. Точное значение корня дать не возможно.
Конечно, данное уравнение не единственное, содержащее логарифмы с разными основаниями. Решить такие уравнения можно только с помощью перехода к новому основанию логарифма. Трудности, связанные с логарифмами разных оснований могут встретиться и в других типах заданий. Например, при сравнении чисел и .
Помощником в решении таких заданий является теорема
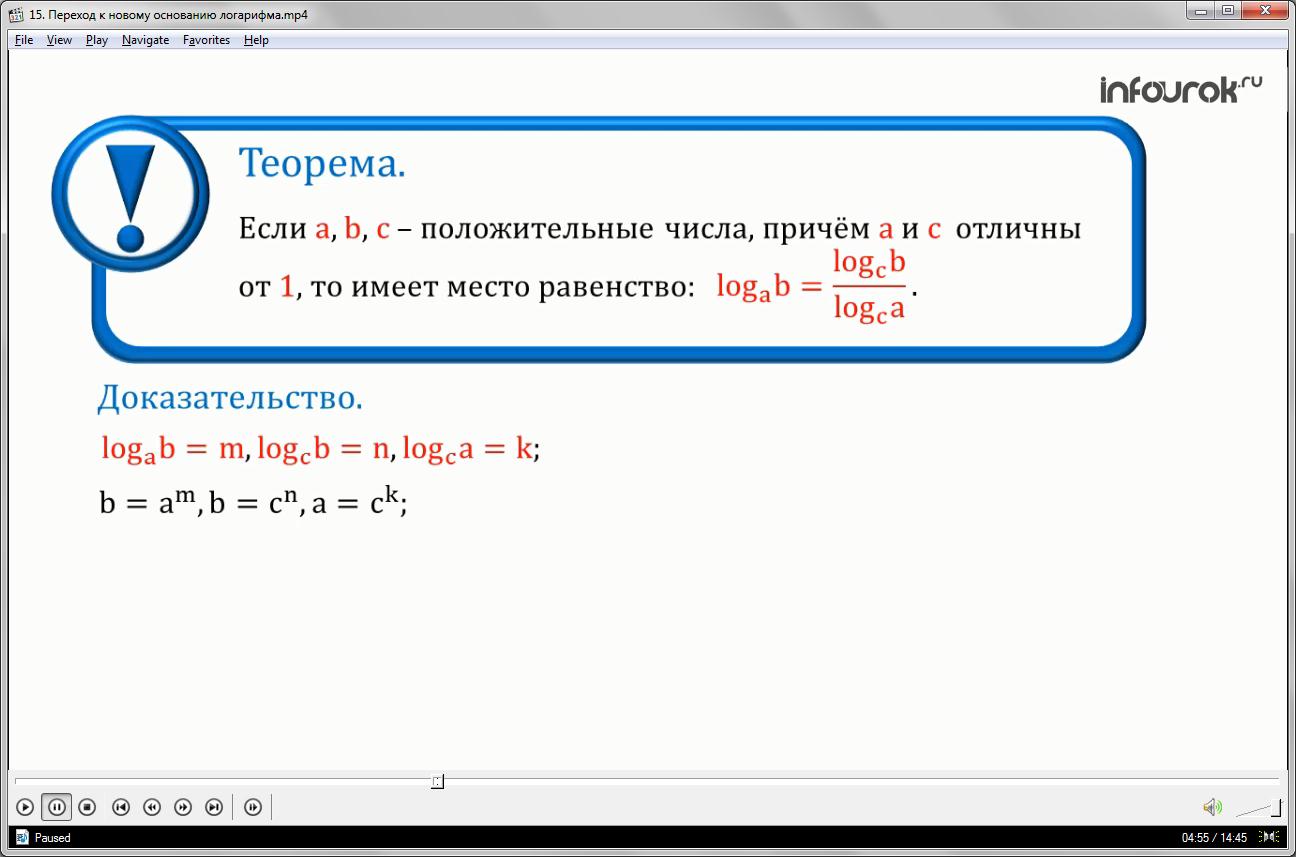
Теорема: Если a,b,c – положительные числа, причём а и с отличны от 1, то имеет место равенство
Эта формула называется – формула перехода к новому основанию)
Таким образом, из и больше . Так как по формуле перехода к новому основанию равен и равен
Докажем теорему о переходе к новому основанию логарифма.
Для доказательства введем обозначения =m, =n, =k(логарифм числа бэ по основанию а равен эм, логарифм числа бэ по основанию цэ равен эн, логарифм числа а по основанию цэ равен ка).Тогда по определению логарифма: число b есть а в степени m, число b есть с в степени n, число a есть с в степени k. Так то подставим её значение в при возведении степени в степень показатели степеней перемножаются, получим , что =, но следовательно = , если основания степени равны, то равны и показатели данной степени=. Значит = вернемся к обратной замене: (логарифм числа бэ по основанию а равен отношению логарифма числа бэ по основанию цэ к логарифму числа а по основанию цэ)
Рассмотрим для данной теоремы два следствия.
Первое следствие. Пусть в данной теореме мы хотим перейти к основанию b. Тогда
(логарифм числа бэ по основанию бэ деленное на логарифм числа а по основанию бэ)
равен единице, то равен
Значит, если aи bположительные и отличные от 1 числа, то справедливо равенство
Следствие 2. Если a и b – положительные числа, причем а не равное единице число, то для любого числа m, не равного нулю, справедливо равенство
логарифм b по основанию а равен логарифму b в степени m по основанию a в степени m.
Докажем данное равенство справа налево. Перейдем в выражении(логарифм числа бэ в степени эм по основанию а в степени эм)к логарифму с основанием а. По свойству логарифма показатель степени подлогарифмического выражения можно вынести вперёд – перед логарифмом. =1. Получим . (дробь, в числителе эм умноженное на логарифм числа бэ по основанию а в знаменателе эм)Число m не равно нулю по условию, значит, полученную дробь можно сократить на m. Получим . Что и требовалось доказать.
Значит, для перехода к новому основанию логарифма используются три формулы
Пример 2. Решить уравнение
(логарифм выражения десять икс минус девять по основанию три равен логарифму икс по основанию одна третья)
Область допустимых значений мы нашли у данного уравнения ранее. Приведем к новому основанию 3. Для этого запишем в данный логарифм в виде дроби. В числителе будет логарифм х по основанию три, в знаменателе будет логарифм одной третьей по основанию три. равен минус одному, тогда правая часть уравнения будет равна минус
Перенесем в левую часть уравнения и запишем как . По свойству, сумма логарифмов равна логарифму произведения, значит (логарифм выражения десять икс минус девять по основанию три плюс логарифм икс по основанию три)можно записать как .(логарифм произведения десять икс минус девять и икс по основанию три) Выполним умножение, получим в левой части уравнения ,
а в правой части — ноль запишем как , так как три в нулевой степени есть один.
Методом потенцирования получим квадратное уравнение =0. По свойству коэффициентов а+b+c=0 корни уравнения равны 1 и 0,1.
Но в области определения лежит только один корень. Это число один.
Пример 3. Вычислить . (три в степени четыре, умноженное на логарифм двух по основанию три плюс логарифм корня из двух по основанию пять умноженное на логарифм двадцати пяти по основанию четыре)
Для начала рассмотрим степень числа три. Если степени умножаются, то выполняется действие возведение степени в степень, таким образом, степень числа три можно записать как три в степени в четвёртой степени. Логарифмы в произведении с разным основанием, удобнее — логарифм с основанием четыре привести к основанию, связанному с пятью. Поэтому заменим на тождественно равное ему выражение . По формуле перехода к новому основанию.
По основному логарифмическому тождеству (а в степени логарифм числа бэ по основанию а равен числу бэ)
вместо получим В выражении выделим квадрат основания и подлогарифмического выражения. Получим . По формуле перехода к новому основанию, она записана справа от решения, получим вместо только . Квадратный корень из двух запишем как два в степени одна вторая и по свойству логарифма вынесем показатель степени перед логарифмом. Получим выражение . Таким образом, вычисляемое выражение примет вид…
При этом это 16, а произведение равно одному, значит значение выражения равно 16,5.
Пример 4. Вычислить , если lg2=a, lg3=b
Для вычисления воспользуемся свойствами логарифма и формулами перехода к новому основанию.
18 представим в виде произведения шести и трех. Логарифм произведения равен сумме логарифмов-множителей, то есть , где равен 1. Так как нам известны десятичные логарифмы, то перейдем от логарифма с основанием 6 к десятичному логарифму, получим дробь в числителе которой (десятичный логарифм трех) а в знаменателе (десятичный логарифм шести). При этом можно уже заменить на b. Разложим шесть на множители два и три. Полученное произведение запишем в виде суммы логарифмов lg2 и lg 3. Заменим их соответственно на aи b. Выражение примет вид: . Если данное выражение преобразовать в дробь путём приведения к общему знаменателю, то ответ получится
Для успешного выполнения заданий, связанных с переходом к новому основанию логарифма, необходимо знать формулы перехода к новому основанию логарифма
- , где a,b,c-положительные числа, a, c
- , где a,b-положительные числа, a, b
- , где a,b-положительные числа a, m
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5925 |
| Номер материала | 1064 |