
Урок "Периодичность функций y=sinx, y=cosx"

Краткое описание документа:
Видеоурок «Периодичность функций у = sin х, у = cos х» раскрывает понятие периодичности функции, рассматривает описание примеров решения задач, в которых используется понятие периодичности функции. Данный видеоурок является наглядным пособием для объяснения темы ученикам. Также данное пособие может стать самостоятельной частью урока, освобождая учителя для проведения индивидуальной работы с учениками.
Наглядность в представлении данной темы очень важна. Чтобы представить поведение функции, построение графика, ее необходимо визуализировать. Произвести построения с помощью классной доски и мела не всегда удается так, чтобы они были понятны всем ученикам. В видеоуроке есть возможность при построении выделять части рисунка цветом, производить преобразования с помощью анимации. Таким образом, построения становятся более понятными большинству учеников. Также возможности видеоурока способствуют лучшему запоминанию материала.
Демонстрация начинается с представления темы урока, а также напоминания ученикам материала, изученного на прошлых уроках. В частности, подытоживается перечень свойств, которые были выявлены в функциях у = sin х, а также у = cos х. Среди свойств рассматриваемых функций отмечены область определения, область значений, четность (нечетность), другие особенности - ограниченность, монотонность, непрерывность, точки наименьшего (наибольшего) значения. Ученикам сообщается, что на данном уроке изучается еще одно свойство функции – периодичность.
Представлено определение периодичной функции y=f(x), где xϵX, в которой выполняется условие f(x-Т)= f(x)= f(x+Т) для некоторого Т≠0. Иначе число Т называют периодом функции.
Для рассматриваемых функций синуса и косинуса выполнение условия проверяется, применяя формулы приведения. Очевидно, что вид тождества sin(x-2π)=sinx=sin(x+2π) соответствует виду выражения определяющего условие периодичности функции. Такое же равенство можно отметить для косинуса cos (x-2π)= cos x= cos (x+2π). Значит, данные тригонометрические функции являются периодическими.
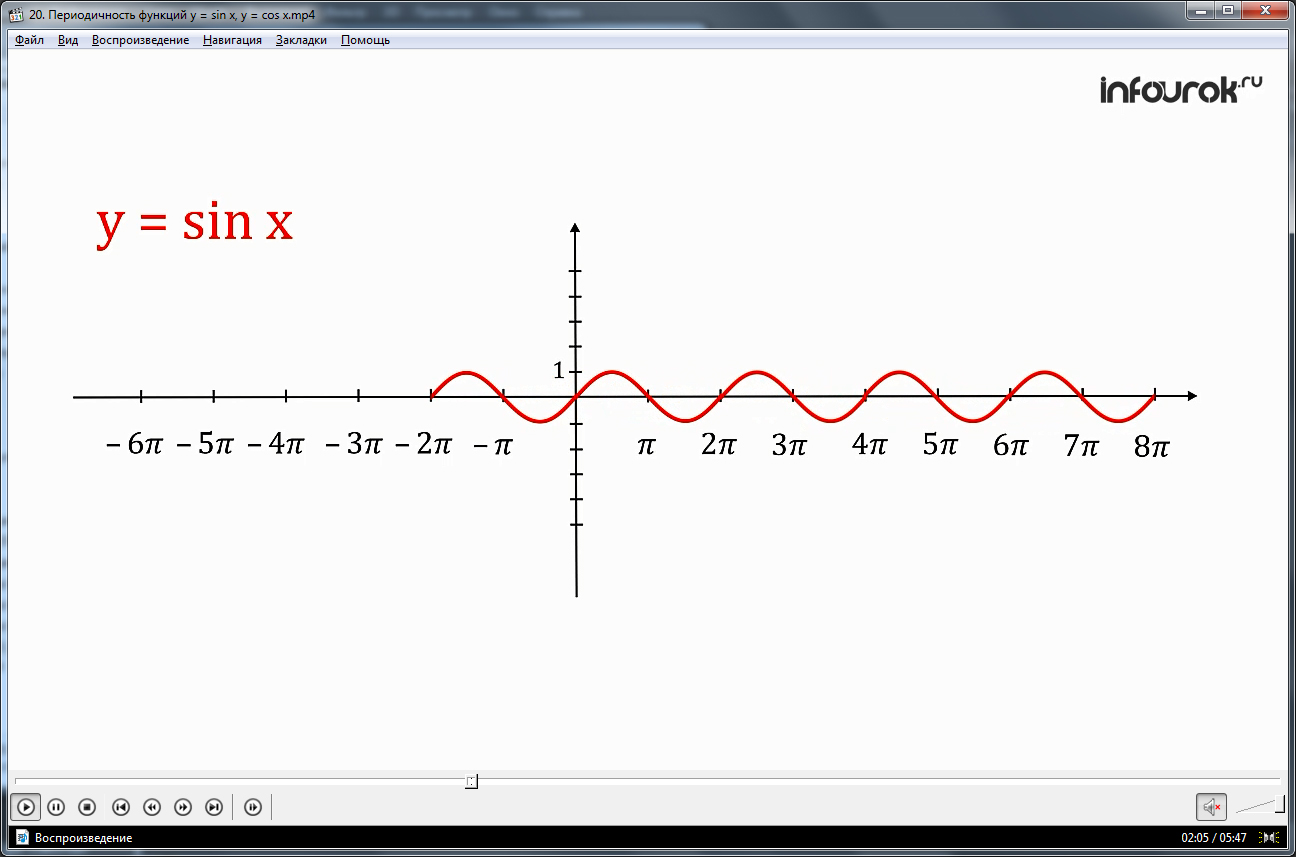
Далее отмечается, как свойство периодичности помогает строить графики периодичных функций. Рассматривается функция у = sin х. На экране строится координатная плоскость, на которой отмечены абсциссы от -6π до 8π с шагом π. На плоскости строится часть графика синуса, представленный одной волной на отрезке [0;2π]. На рисунке демонстрируется, как график функции формируется на всей области определения сдвигом построенного фрагмента, и получая длинную синусоиду.
Строится график функции у = cos х, используя свойство ее периодичности. Для этого на рисунке строится координатная плоскость, на которой изображается фрагмент графика. Отмечается, что обычно такой фрагмент строится на отрезке [-π/2;3π/2]. Аналогично графику функции синуса, построение графика косинуса выполняется сдвигом фрагмента. В результате построения образуется длинная синусоида.
Построение графика периодичной функции имеет особенности, которые можно использовать. Поэтому они даются в обобщенном виде. Отмечается, что для построения графика такой функции сначала строят ветвь графика на некотором промежутке длиной Т. затем необходимо сдвинуть построенную ветвь вправо и влево на Т, 2Т, 3Т и т.д. при этом указывается еще на одну особенность периода – для любого целого k≠0 число kТ также является периодом функции. Однако Т называется основным периодом, так как он наименьших из всех. Для тригонометрических функций синуса и косинуса основным периодом является 2π. Однако также являются периодами 4π, 6π и т.д.
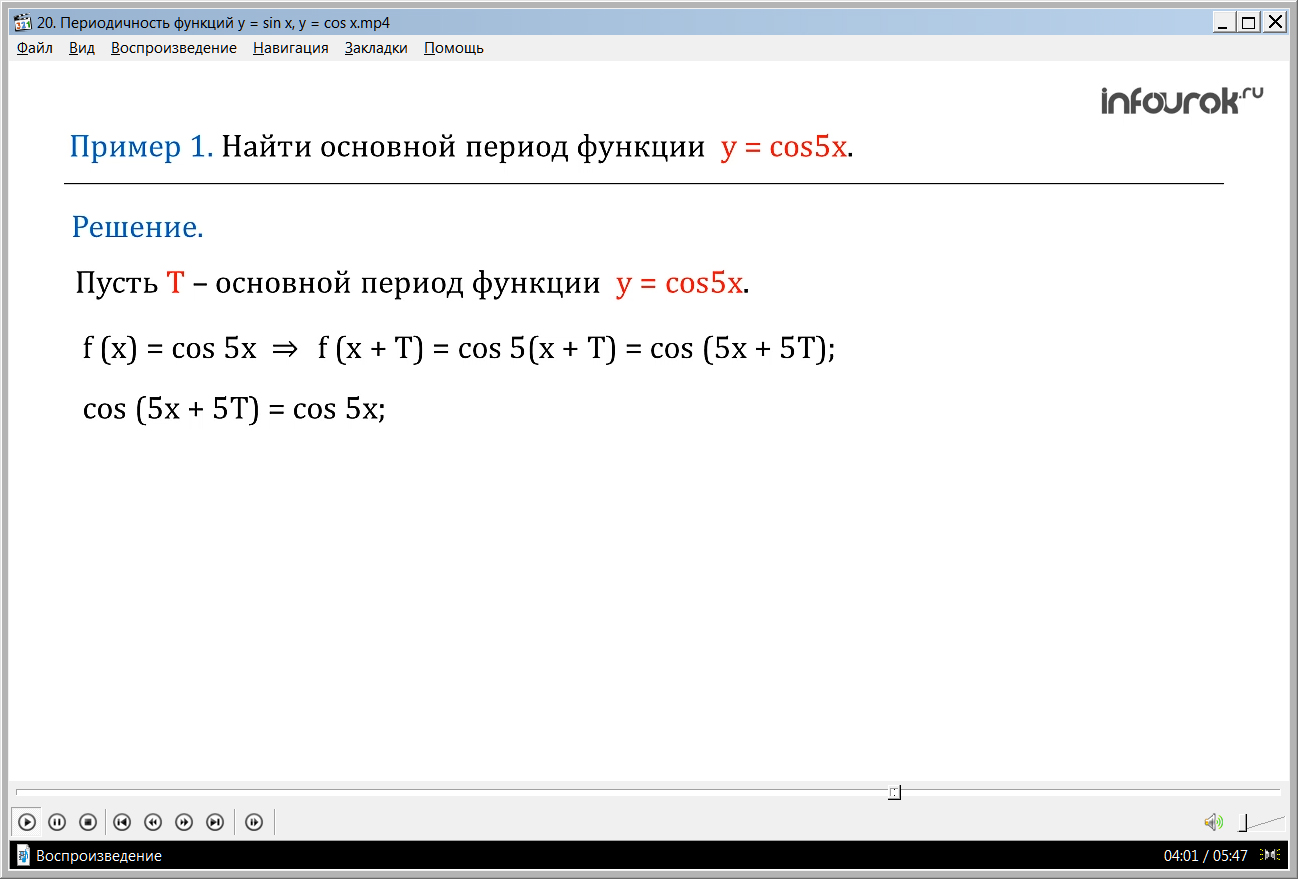
Далее предлагается рассмотреть нахождение основного периода функции у = cos 5х. Решение начинается с предположением, что Т – период функции. Значит, необходимо выполнение условия f(x-Т)= f(x)= f(x+Т). В данном тождестве f(x)= cos 5х, а f(x+Т)=cos 5(x+Т)= cos (5x+5Т). При этом cos (5x+5Т)= cos 5х, следовательно 5Т=2πn. Теперь можно найти Т=2π/5. Задача решена.
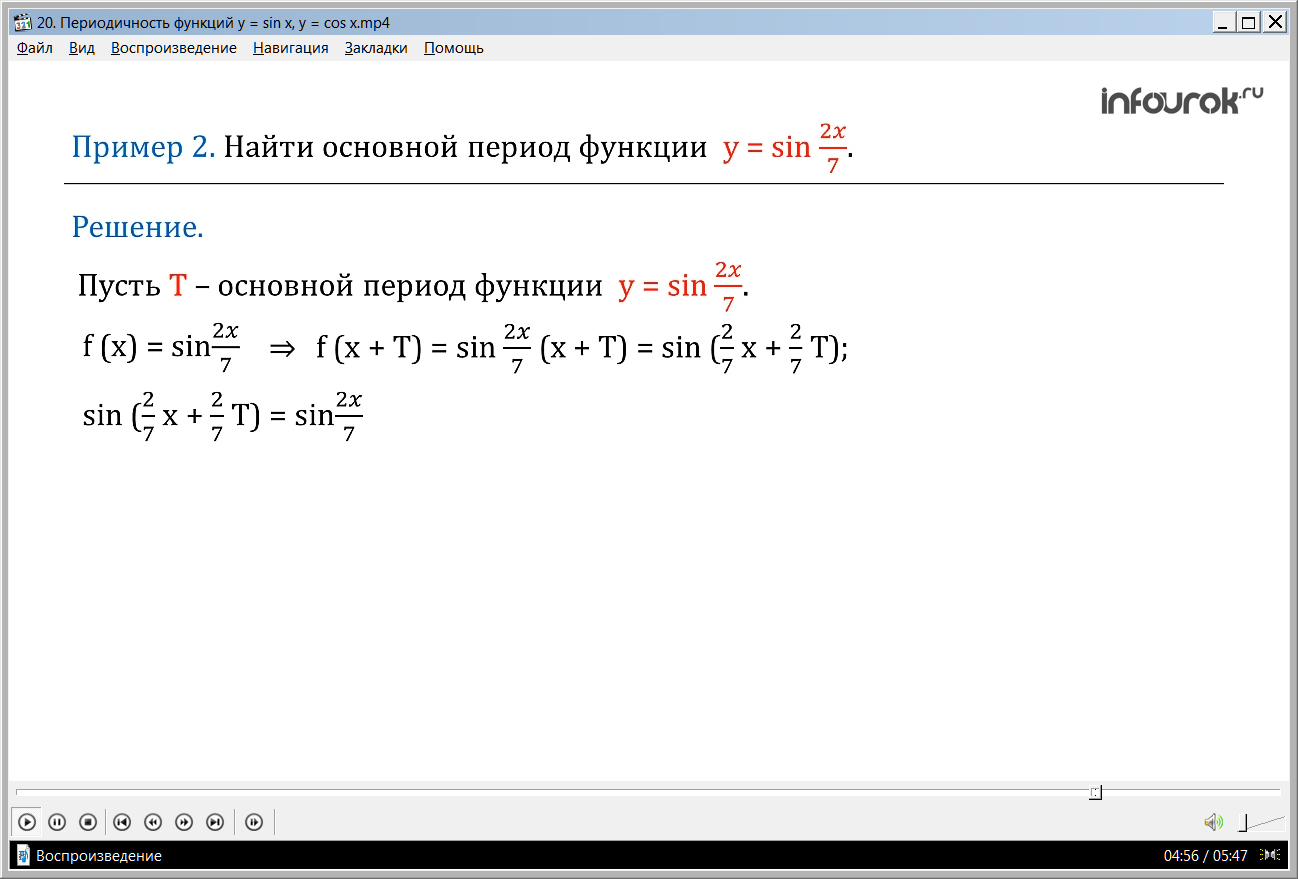
Во второй задаче необходимо найти основной период функции y=sin(2x/7). Предполагается, что основной период функции Т. для данной функции f(x)= sin(2x/7), а через период f(x+Т)=sin(2x/7)(х+Т)= sin(2x/7+(2/7)Т). после приведения получаем (2/7)Т=2πn. Однако нам необходимо найти основной период, поэтому берем наименьшее значение (2/7)Т=2π, из которого находим Т=7π. Задача решена.
В конце демонстрации результаты примеров обобщаются, сформировав правило для определения основного периода функции. Отмечается, что для функций у=sinkxи y=coskx основными периодами являются 2π/k.
Видеоурок «Периодичность функций у = sin х, у = cos х» может применяться на традиционном уроке математики для повышения эффективности урока. Также данный материал рекомендуется использовать учителю, осуществляющему дистанционное обучение для повышения наглядности объяснения. Видео может быть рекомендовано отстающему ученику для углубления понимания темы.
ТЕКСТОВАЯ РАСШИФРОВКА:
«Периодичность функций у = cos x, y =sin x».
Для построения графиков функций y =sin x и у = cos x были использованы свойства функций:
1 область определения,
2 область значения,
3 четность или нечетность,
4 монотонность,
5 ограниченность,
6 непрерывность,
7 наибольшее и наименьшее значение.
Сегодня мы изучим еще одно свойство: периодичность функции.
ОПРЕДЕЛЕНИЕ. Функцию у = f ( x), где х ϵ Х( игрек равно эф от икс, где икс принадлежит множеству икс), называют периодической, если существует отличное от нуля число Т такое, что для любого х из множества Х выполняется двойное равенство: f ( x – Т)= f ( x) = f ( x + Т)( эф от икс минус тэ равно эф от икс и равно эф от икс плюс тэ). Число Т, которое удовлетворяет такому двойному равенству, называют периодом функции
у = f ( x).
А так как синус и косинус определены на всей числовой прямой и для любого х выполняются равенства sin( x – 2π)= sin x= sin( x+ 2π) ( синус от икс минус два пи равен синусу икс и равен синусу от икс плюс два пи) и
cos ( x– 2π)= cos x = cos ( x+ 2π) ( косинус от икс минус два пи равен косинусу икс и равен косинусу от икс плюс два пи), то синус и косинус – это периодические функции с периодом 2π.
Периодичность позволяет быстро построить график функции. Ведь для того, что бы построить график функции y = sin x , достаточно построить одну волну (чаще всего на отрезке [0; 2π] (от нуля до двух пи), а затем с помощью сдвига построенной части графика вдоль оси абсцисс вправо и влево на 2π, затем на 4π и так далее получить синусоиду.
(показать сдвиг вправо и влево на 2π, 4π)
Аналогично для графика функции
у = cos x, только строим одну волну чаще всего на отрезке [; ] (от минус пи на два до трех пи на два).
Обобщим выше сказанное и сделаем вывод: для построения графика периодической функции с периодом Т сначала нужно построить ветвь( или волну, или часть) графика на любом промежутке длины Т( чаще всего это промежуток с концами в точках 0 и Т или же – и (минус тэ на два и тэ на два), а затем сдвинуть эту ветвь вдоль оси х( икс) вправо и влево на Т, 2Т, 3Т и т. д.
Очевидно, что если функция периодическая с периодом Т, то при любом целом k0( ка не равном нулю) число вида kT( ка тэ) тоже период этой функции. Обычно стараются выделить наименьший положительный период, который называют основным периодом.
В качестве периода функций у = cos x, y = sin x можно было бы взять – 4π, 4π,– 6π, 6π и т.д.( минус четыре пи, четыре пи, минус шесть пи, шесть пи и так далее). Но число 2π является основным периодом и той, и другой функции.
Рассмотрим примеры.
ПРИМЕР 1.Найти основной период функции у = сos5x (игрек равно косинус пяти икс).
Решение. Пусть Т – основной период функции у = сos5x. Положим
f (x) = сos5x, тогда f (x + Т)= сos5(x + Т)= сos (5x + 5Т) ( эф от икс плюс тэ равно косинусу пяти, умноженного на сумму икса и тэ равно косинусу от суммы пяти икс и пяти тэ).
Чтобы число Т было периодом функции, должно выполнятся тождество
сos (5x + 5Т)= сos5x. Отсюда 5Т= 2πn (пять тэ равно два пи эн), но по условию нужно найти основной период, значит, 5Т= 2π. Получаем Т=
( период данной функции равен два пи, деленное на пять).
Ответ: Т=.
ПРИМЕР 2. Найти основной период функции у = sin ( игрек равно синус частного двух икс на семь).
Решение. Пусть Т – основной период функции у = sin . Положим
f ( x) = sin , тогда f ( x + Т)= sin ( x + Т) = sin ( x + Т) ( эф от икс плюс тэ равно синусу произведения двух седьмых и суммы икса и тэ равно синусу от суммы двух седьмых икс и двух седьмых тэ).
Чтобы число Т было периодом функции, должно выполнятся тождество
sin ( x + Т) = sin . Отсюда Т= 2πn (две седьмые тэ равно два пи эн), но по условию нужно найти основной период, значит, Т= 2π. Получаем Т=7
( период данной функции равен семи пи).
Ответ: Т=7.
Обобщая результаты, полученные в примерах, можно сделать вывод: основной период функций y =sin kx или у = cos kx (игрек равно синус ка икс или игрек равно косинус ка икс) равен (два пи, деленное на ка).
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 22456 |
| Номер материала | 843 |