
Урок «Первообразная»

Краткое описание документа:
На прошлых занятиях вы познакомились с правилами нахождения производной функции, узнали о применении производной для исследования функции на монотонность и экстремум; научились находить касательную к графику функции.
Вспомним правила вычисления производных:
Производная любого числа равна нулю.
Производная икса равна единице.
Производная ка икс плюс эм равна ка.
Производная единицы, делённой на икс, равна минус единице, делённой на икс в квадрате.
Производная корень из икс равна единице, делённой на два корень из икс.
Производная синуса икс равна косинус икс.

Производная косинуса икс равна минус синус икс.
Производная икс в степени эн равна эн, умноженное на икс в степени эн минус один.
Иногда приходится решать и обратные задачи, к примеру, восстановить закон движения по известной скорости.
В математике принято взаимно обратным операциям присваивать специальные названия.
Например, операция, обратная умножению, — это деление.
Операция извлечения квадратного корня обратна возведению в квадрат.
Процесс нахождения производной заданной функции называется дифференцированием, а операция, обратная ей, — интегрированием (процесс нахождения функции по данной производной).
То есть функцию, выступающую как бы родоначальником для производной данной функции, принято называть первообразной.
Определение: функцию игрек равное эф большое от икс называют первообразной для функции игрек равное эф малое от икс на заданном промежутке икс большое, если для любого икс, принадлежащего данному промежутку, выполнено равенство:
Промежуток, которому принадлежит икс, обычно не указывают, но подразумевают.
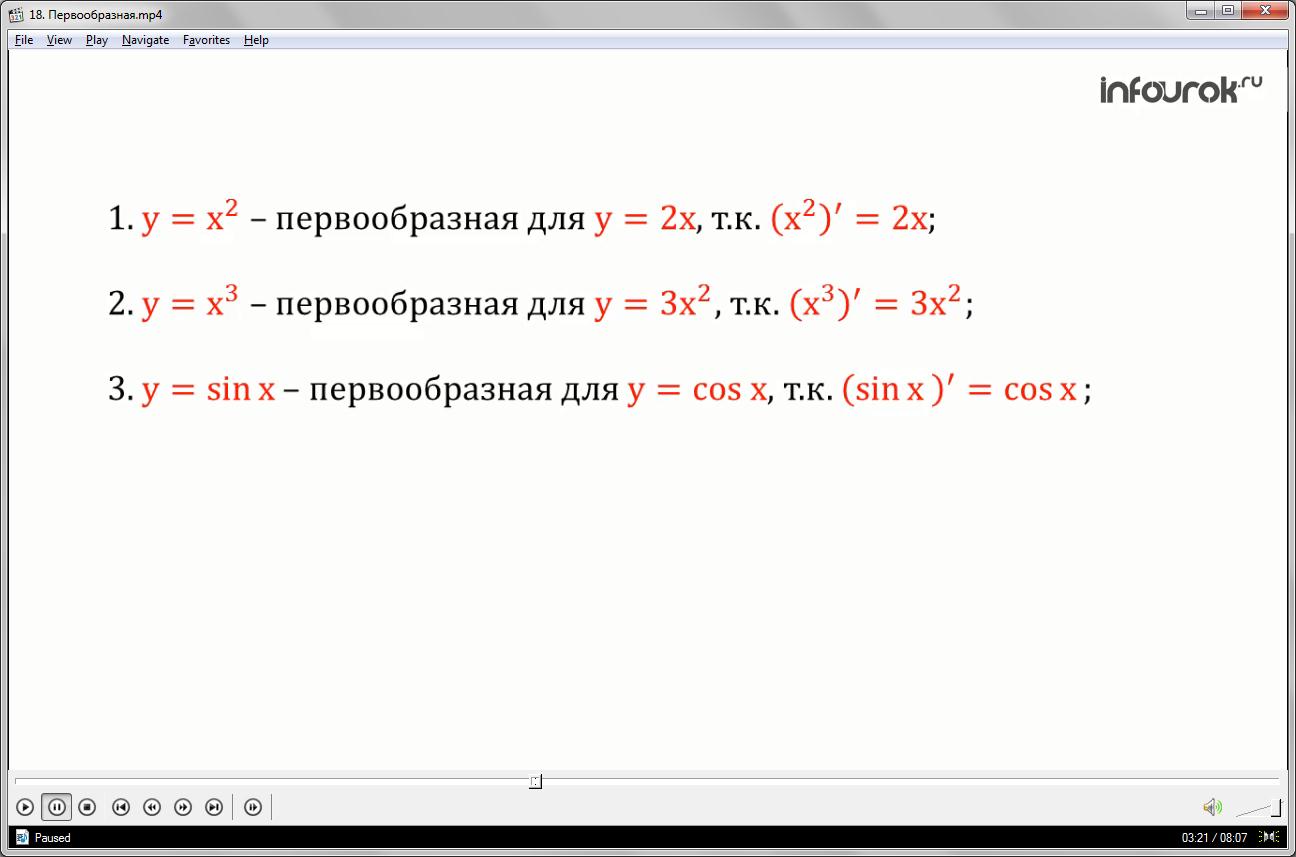
Рассмотрим примеры.
1.Функция игрек, равное икс в квадрате, является первообразной для функции игрек, равное два икс, так как для любого икс справедливо равенство: производная икс в квадрате равна два икс.
2. Функция игрек, равное икс в кубе, является первообразной для функции игрек, равное три икс в квадрате, так как для любого икс справедливо равенство: производная икс в кубе равна три икс в квадрате.
3.Функция игрек, равное синус икс, является первообразной для функции игрек, равное косинус икс, так как для любого икс выполняется равенство: производная синуса икс равна косинус икс.
4.Функция игрек, равное корень из икс, является первообразной для функции игрек, равное один, делённое на два корень из икс, на промежутке от нуля до бесконечности, так как для любого икс больше нуля выполняется равенство: производная корень из икс равна единице, делённой на два корень из икс.
Зная формулы для нахождения производных, не сложно составить таблицу первообразных:
1.Первообразная нуля равна константе.
2.Первообразная единицы равна икс.
3.Первообразная для икс равна икс в квадрате, делённое на два.
4. Первообразная для функции икс в степени эн, эн принадлежит множеству натуральных чисел, равна икс в степени эн плюс один, делённое на эн плюс один.
5.Первообразная для функции один, делённое на икс в квадрате, равна минус один, делённое на икс.
6.Первообразная для функции один, делённое на корень из икс равна два корень из икс, причём икс больше нуля.
7. Первообразная для функции синус икс равна минус косинус икс.
8. Первообразная для функции косинус икс равна синус икс.
9. Первообразная для функции один, делённое на синус в квадрате икс, равна минус котангенс икс.
10. Первообразная для функции один, делённое на косинус в квадрате икс, равна тангенс икс.

Рассмотрим примеры на нахождение первообразной различных функций.
Задание 1
Доказать, что функция является первообразной для функции , если первообразная функции равна икс в шестой степени, сама функция равна шесть икс в пятой степени.
Решение:
1. По определению первообразной, функцию игрек, равное эф большое от икс, называют первообразной для функции игрек, равное эф малое от икс, на заданном промежутке икс большое, если для любого икс, принадлежащего данному промежутку, выполнено равенство: .
2. Найдём производную эф большое по формуле нахождения производной степенной функции , она равна шесть икс в пятой степени.
Мы получили равенство двух выражений, значит, по определению первообразной, функция эф большое, равная икс в шестой степени, является первообразной для функции эф малая, равной шесть икс в пятой степени.
Задание 2
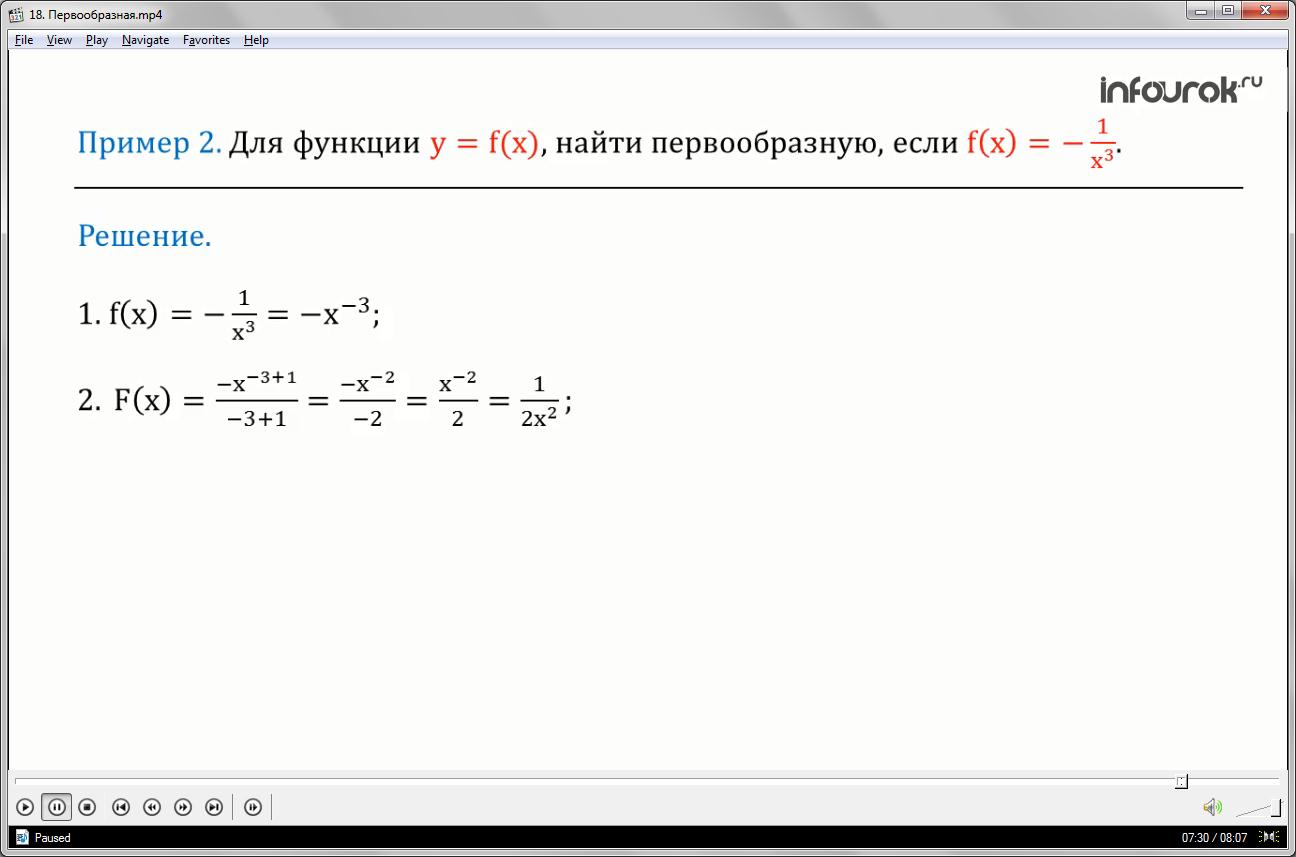
Для функции (игрек, равное эф от икс малое) найти первообразную, если
(эф от икс равно минус один, делённое на икс в кубе).
Решение:
1.По определению степени с целым отрицательным показателем представим выражение минус один, делённое на икс в кубе, в виде: минус икс в минус третьей степени.
2. По формуле нахождения первообразной степенной функции, найдём первообразную для функции эф от икс, равное минус икс в минус третьей степени.
Получим, минус икс в степени минус три плюс один, делённое на минус три плюс один.
Упрощая выражение, имеем минус икс в степени минус два, делённое на минус два, сократив минусы, получаем: икс в степени минус два, делённое на два.
По определению степени с целым отрицательным показателем представим выражение в виде: один, делённое на два икс в квадрате.
Таким образом, первообразной для функции эф от икс малое, равной минус один, делённое на икс в кубе, является функция эф большое, равная один, делённое на два икс в квадрате.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 16939 |
| Номер материала | 1067 |