
Урок "Пирамида"

Краткое описание документа:
Видеоурок «Пирамида» предназначен для представления учебного материала по денной теме в курсе геометрии 9 класса. В ходе видеоурока раскрывается, каким образом образуется геометрическое тело пирамида, рассматриваются ее составляющие элементы, свойства и формула для нахождения объема. Задача данного видеоурока – сформировать представление учеников о пирамиде с точки зрения стереометрии, формировать умение доказывать математические утверждения, используя наглядность в представлении учебного материала, способствовать лучшему усвоению и запоминанию понятий и утверждений.
При помощи анимации сделанные для демонстрации видео построений представлены максимально приближенно к традиционным построениям на доске. Также анимация помогает подавать учебный материал ярко и последовательно. Те формулировки и понятия, которые требуют лучшего запоминания - выделяются цветом и озвучиваются. Благодаря нестандартному представлению материала на изучаемом предмете легче удержать внимание учеников. Видеоурок способствует повышению эффективности обучения, дает возможность освободить учебное время для усиления индивидуальной работы или решения других учебных задач.
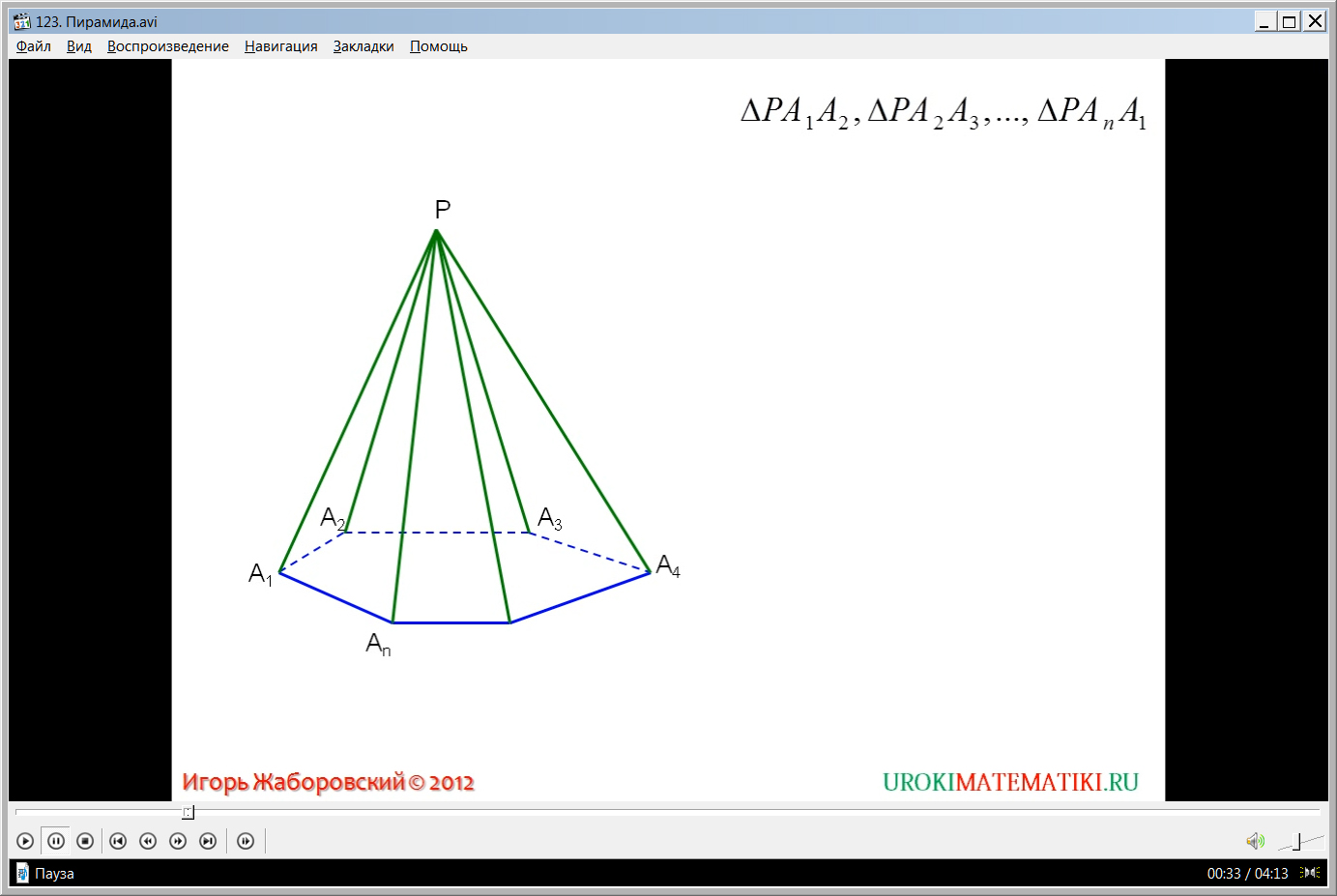
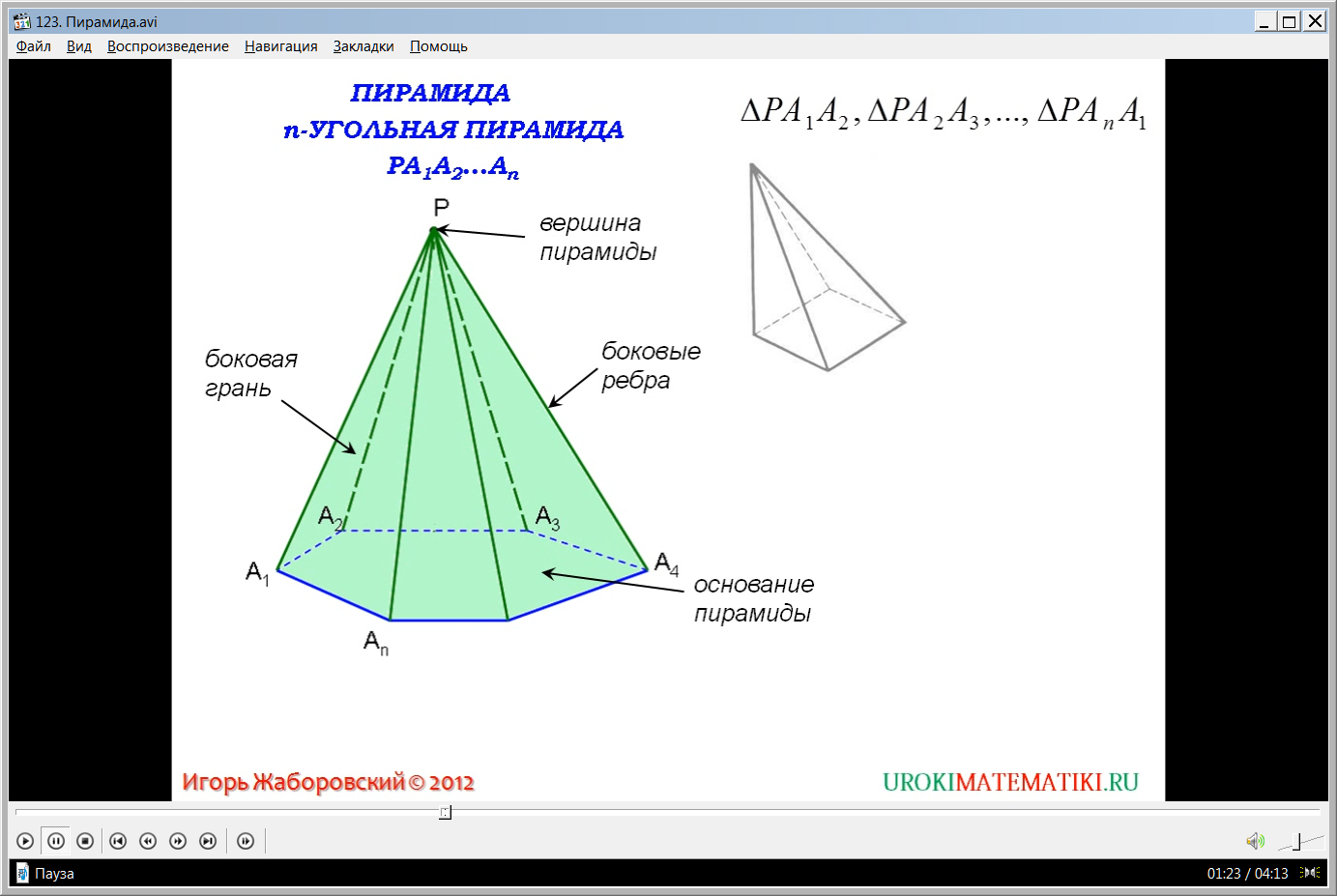
Видеоурок начинается с представления названия темы. На экране изображается многоугольник А1А2А3…An, расположенный на некоторой плоскости. Также изображается некоторая точка Р, не лежащая в плоскости многоугольника. При соединении точки Р и вершин многоугольника А1А2А3…An образуется геометрическая фигура, которая ограничена многоугольником А1А2А3…An и треугольниками РА1А2, РА2А3 и т.д. отмечается, что многогранник, который составлен из построенного многоугольника и данных треугольников, называется пирамидой. Отмечается, что при этом многоугольник А1А2А3…An является основанием пирамиды, а треугольники, составляющие боковую поверхность, называются боковыми гранями пирамиды. Точка Р, которую соединяли с вершинами многоугольника, является вершиной пирамиды, а отрезки соединения называются боковыми ребрами. Все названия выведены при помощи указателей, чтобы их легче было запомнить. При этом отмечается, что от числа углов в многоугольнике пирамиды зависит и ее название. Так как в многоугольнике основания nуглов, данную пирамиду называют n-угольной.
Также приводятся примеры пирамид с различным количеством углом многоугольника – на рисунке изображены четырехугольная , шестиугольная пирамиды, треугольная. Сообщается, что иначе треугольная пирамида нередко называется тетраэдром.
На рисунке строится высота пирамиды РН. Отмечается, что высотой в данном случае называется перпендикуляр, проведенный из вершины Р к основанию пирамиды – многоугольнику А1А2А3…An. Определение высоты пирамиды выедено на экран и выделено для запоминания.
Далее представлено определение правильной пирамиды, как пирамиды в основании которой лежит правильный многоугольник, а высота является отрезком, соединяющим вершину пирамиды с центром многоугольника. Также на рисунке пирамиды отмечается апофема – высота ее боковой грани. Определение апофемы выделено на экране для запоминания и озвучено. Также отмечается, что все апофемы правильной пирамиды юудутт равными друг другу. Это утверждение легко доказать.
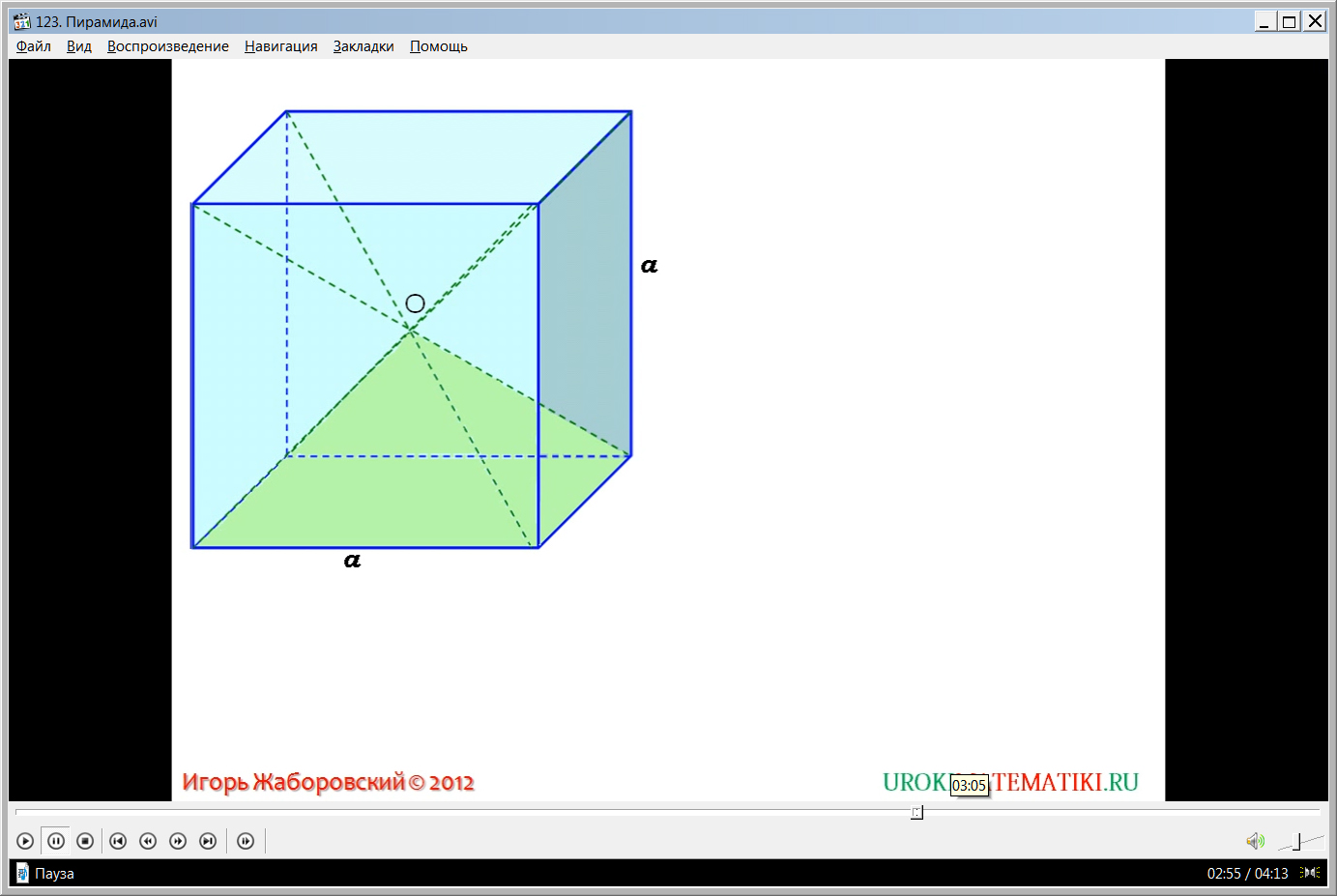
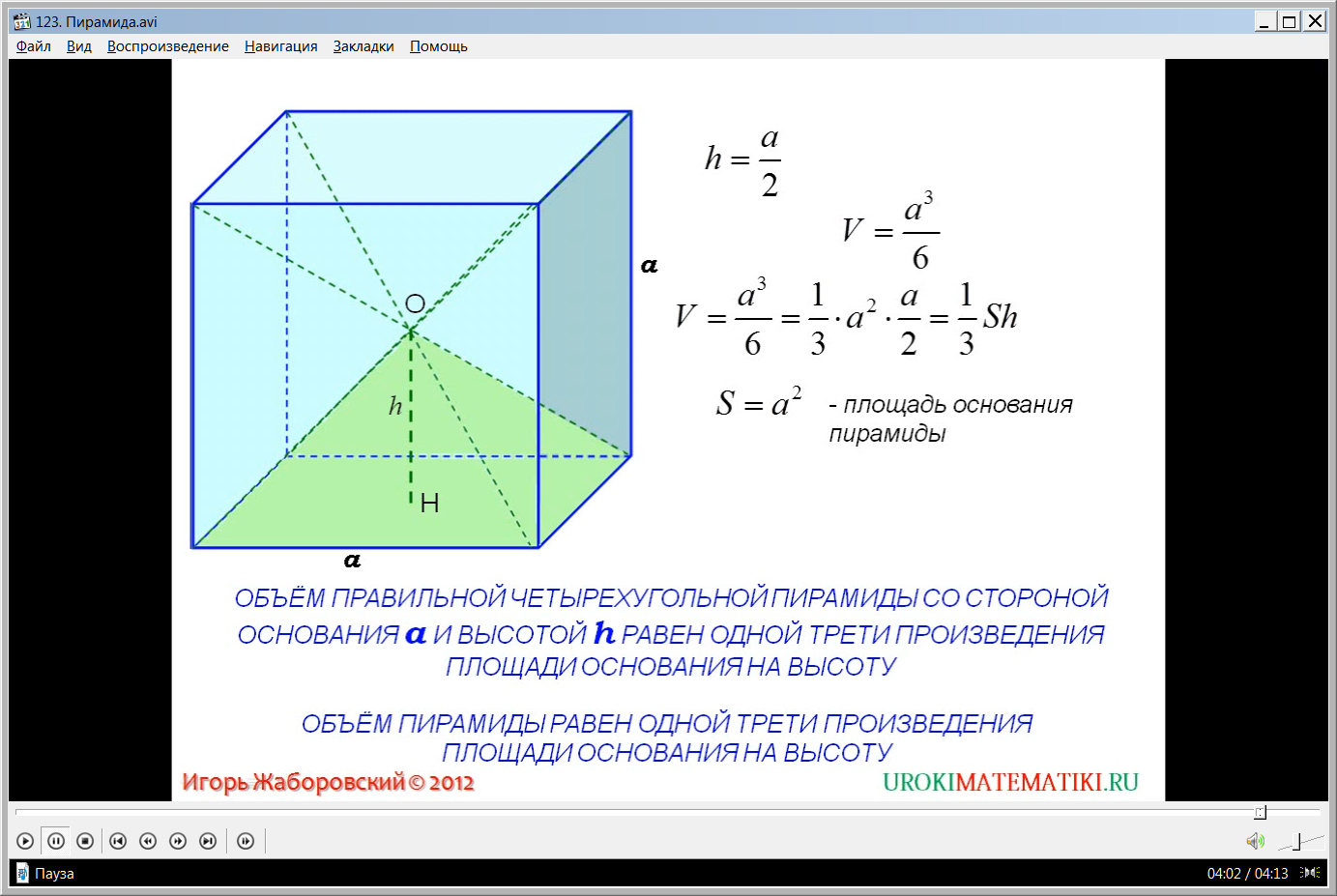
На экране строится куб со стороной а. В данном кубе строятся диагонали. При помощи построенных диагоналей внутри куба образуются четыре пирамиды с общей вершиной в точке О, являющейся центром куба. Отмечается, что в каждой пирамиде основанием является квадрат, сторона которого равна а, высота равна половине стороны а, то есть h=a/2. Также отмечено, что формула для определения объема пирамиды V=a3/6. Однако в данной формуле замечено, что она разбивается на произведение (1/3)*а2*а/2. Подставив значения данных выражений, где а2 – площадь основания, а/2 – высота пирамиды, получаем новую формулу для определения объема V=(1/3)Sh. Из данного доказательства получаем вывод о том, что для вычисления объема правильной 4-угольной пирамиды, можно использовать формулу V=(1/3)Sh. Также отмечается, что аналогично данному ходу рассуждения производится доказательство утверждения, что для любой пирамиды формула для вычисления объема V=(1/3)Sh будет справедливой.
Видеоурок «Пирамида» может использоваться на традиционном уроке математики для повышения его эффективности. Также видеоматериал является ценным инструментом для осуществления дистанционного обучения. Если ученикам необходим дополнительный материал для усвоения темы урока, видео станет незаменимым помощником, помогающим освоить предмет.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4703 |
| Номер материала | 737 |