
Урок «Показательная функция, ее свойства и график»

Краткое описание документа:
Найдем значение выражения при различных рациональных значениях переменной х=2; 0; -3; -
Заметим, какое бы число вместо переменной икс мы не подставили, всегда можно найти значение данного выражения. Значит, мы рассматриваем показательную функцию (игрек равен три в степени икс), определенную на множестве рациональных чисел: .
Построим график данной функции , составив таблицу ее значений.
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
у |
1 |
9 |
Отметим полученные точки на координатной плоскости.
Проведем плавную линию, проходящую через данные точки (рис 1)
Используя график данной функции, рассмотрим ее свойства:
1. Область определения – множество всех действительных чисел.
2.Не является ни четной, ни нечетной.
3.Возрастает на всей области определения.
4.Не имеет ни наибольшего, ни наименьшего значений.
5.Ограничена снизу, но не ограничена сверху.
6.Непрерывна на всей области определения.
- область значения от нуля до плюс бесконечности.
8. Функция выпукла вниз.
Если в одной системе координат построить графики функций ; у=(игрек равен два в степени икс, игрек равен пять в степени икс, игрек равен семь в степени икс), то можно заметить, что они обладают теми же свойствами, что и у=(игрек равен трем в степени икс) (рис.2), то есть такими свойствами будут обладать все функции вида у=(игрек равен а в степени икс, при а большем единицы)
Построим график функции :
1. Составив таблицу ее значений.
|
х |
0 |
1 |
-1 |
2 |
-2 |
3 |
-1 |
|
у |
1 |
3 |
9 |
27 |
Отметим полученные точки на координатной плоскости.
Проведем плавную линию, проходящую через данные точки ( рис 3).
Используя график данной функции, укажем ее свойства:
1. Область определения – множество всех действительных чисел.
2.Не является ни четной, ни нечетной.
3.Убывает на всей области определения.
4.Не имеет ни наибольшего, ни наименьшего значений.
5.Ограничена снизу, но не ограничена сверху.
6.Непрерывна на всей области определения.
7. область значения от нуля до плюс бесконечности.
8. Функция выпукла вниз.
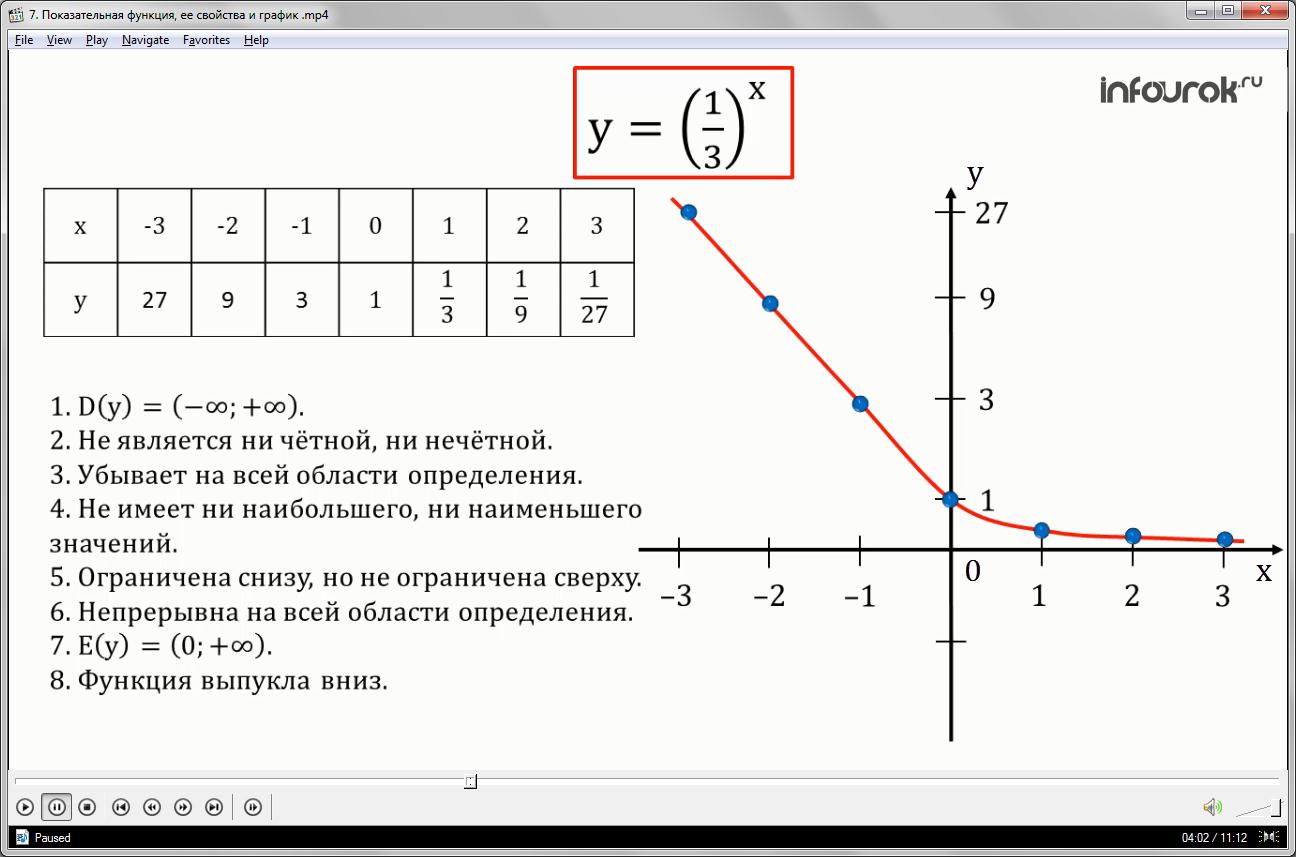
Аналогично, если в одной системе координат построить графики функций ; у=(игрек равен одна вторая в степени икс, игрек равен одна пятая в степени икс, игрек равен одна седьмая в степени икс), то можно заметить, что они обладают теми же свойствами, что и у=(игрек равен одна третья в степени икс)(рис.4), то есть такими свойствами будут обладать все функции вида у=(игрек равен единица, деленная на а в степени икс, при а большем нуля, но меньшем единицы)
Построим в одной системе координат графики функций
значит, будут симметричны и графики функций у=у= (игрек равен а в степени икс и игрек равен единице, деленной на а в степени икс) при одном и том же значении а.
Обобщим сказанное, дав определение показательной функции и указав ее основные свойства:
Определение: Функция вида у=, где (игрек равен а в степени икс, где а положительно и отлично от единицы), называют показательной функцией.
Необходимо запомнить различия между показательной функцией у= и степенной функцией у=, а=2,3,4,…. как на слух, так и зрительно. У показательной функции х является степенью, а у степенной функции х является основанием.
Пример1: Решите уравнение (три в степени икс равно девяти)
В одной системе координат построим два графика функции у= (игрек равняется три в степени икс и игрек равняется девяти) рис.7
Заметим, что они имеют одну общую точку М (2;9) (эм с координатами два; девять), значит, абсцисса точки будет являться корнем данного уравнения. То есть, уравнение имеет единственный корень х= 2.
Пример 2: Решите уравнение
В одной системе координат построим два графика функции у= (игрек равен пяти в степени икс и игрек равен одна двадцать пятая) рис.8. Графики пересекаются в одной точке Т (-2;(тэ с координатами минус два; одна двадцать пятая). Значит, корнем уравнения является х=-2(число минус два).
Пример 3: Решите неравенство
В одной системе координат построим два графика функции у=
(игрек равен три в степени икс и игрек равен двадцати семи).
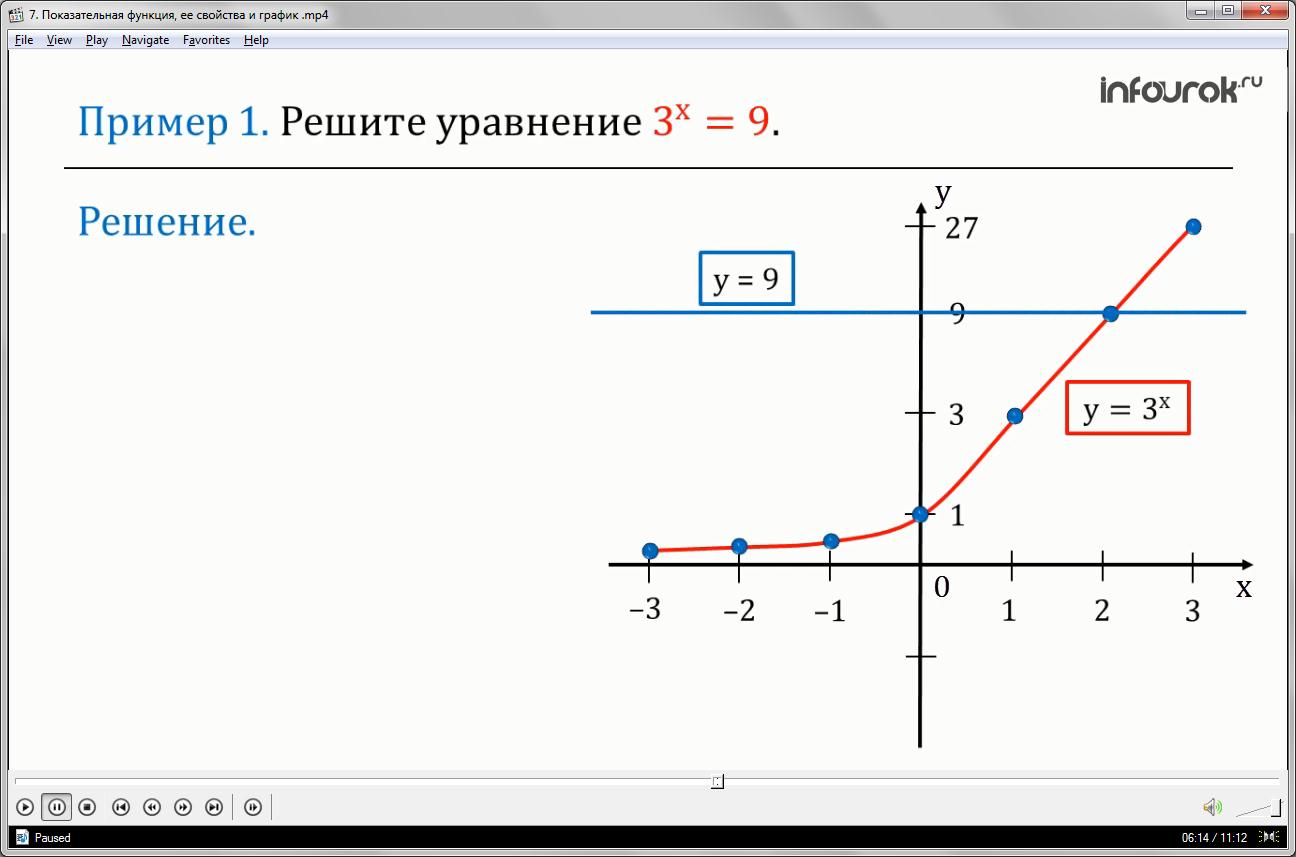
Рис.9 График функции расположен выше графика функции у=при
х Следовательно, решением неравенства является интервал (от минус бесконечности до трех)
Пример 4: Решите неравенство
В одной системе координат построим два графика функции у= (игрек равен одна четвертая в степени икс и игрек равен шестнадцати). (рис.10). Графики пересекаются в одной точке К (-2;16). Значит, решением неравенства является промежуток (-2;(от минус двух до плюс бесконечности), т.к. график функции у=расположен ниже графика функции при х
Наши рассуждения позволяют убедиться в справедливости следующих теорем:
Терема 1: Если справедливо тогда и только тогда, когда m=n.
Теорема 2: Если справедливо тогда и только тогда, когда , неравенство справедливо тогда и только тогда, когда ( рис. *)
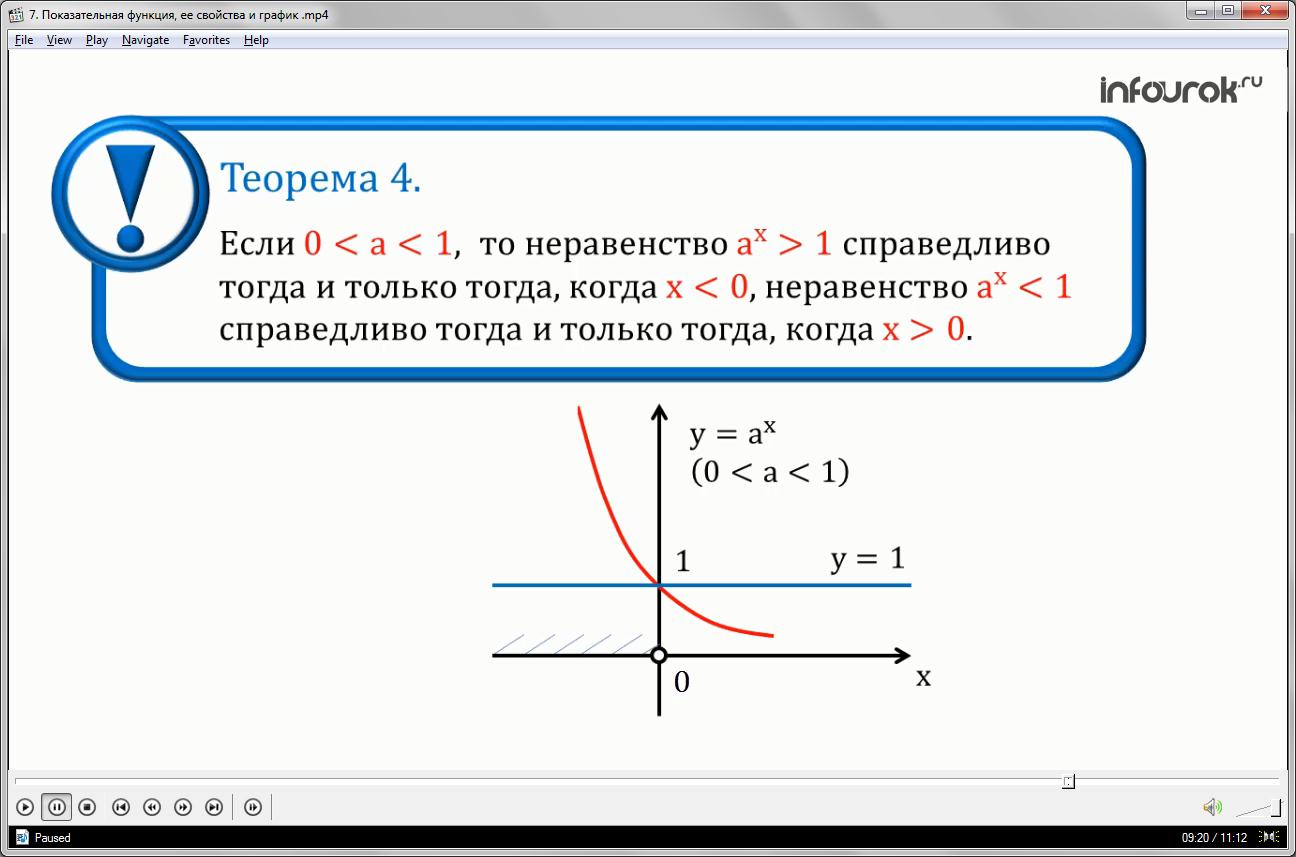
Теорема 4: Если справедливо тогда и только тогда, когда (рис.**), неравенство справедливо тогда и только тогда, когда .Теорема 3: Если справедливо тогда и только тогда, когда m=n.
Пример 5: Построить график функции у=
Видоизменим функцию, применив свойство степени у=
Построим дополнительную систему координат и в новой системе координат построим график функции у= (игрек равен два в степени икс) рис.11.
Пример 6: Решите уравнение
В одной системе координат построим два графика функции у=
(игрек равен семи в степени икс и игрек равен восемь минус икс) рис.12.
Графики пересекаются в одной точке Е (1;(е с координатами один; семь). Значит, корнем уравнения является х=1(икс равный единице).
Пример 7: Решите неравенство
В одной системе координат построим два графика функции у=
(игрек равен одна четвертая в степени икс и игрек равен икс плюс пять). График функции у=расположен ниже графика функции у=х+5 при , решением неравенства является интервал х(от минус единицы до плюс бесконечности).
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10387 |
| Номер материала | 1056 |