
Урок «Показательные неравенства»

Краткое описание документа:
Показательными неравенствами называют неравенства вида
(а в степени эф от икс больше а в степени же от икс, где а-положительное число, отличное от единицы)
и неравенства, сводящиеся к этому виду.
Теорема: Показательное неравенство равносильно неравенству того же смысла
(если основание больше единицы);
показательное неравенство равносильно неравенству противоположного смысла , если (если основание меньше единицы, но больше нуля).
Докажем теорему:
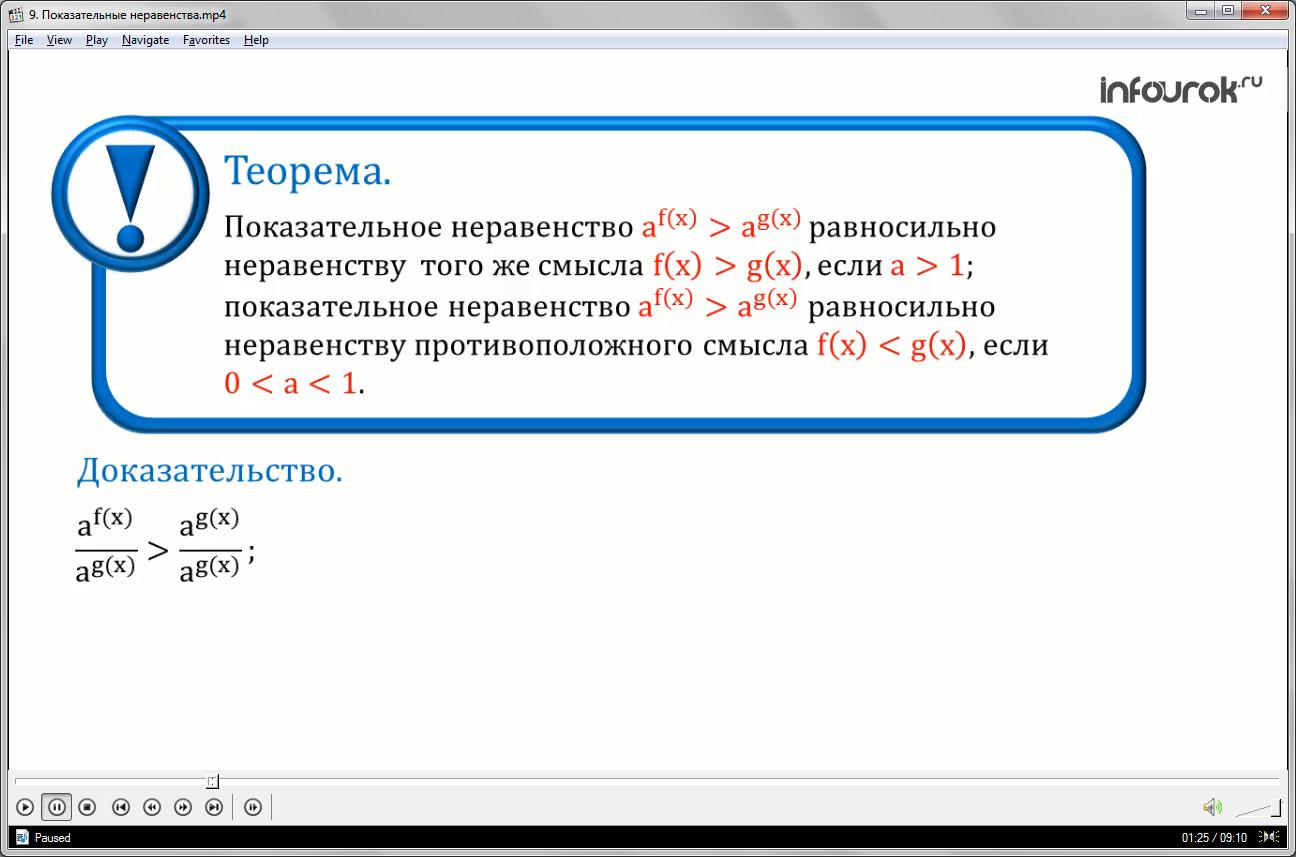
Разделим обе части неравенства на (а в степени же от икс), так как это показательная функция,
Получим значит, ее значения всегда положительны.
(если основание больше единицы), то показательная функция является возрастающей и данное неравенство равносильно f(x)-g(x)
откуда следует
если (если основание меньше единицы, но больше нуля), то показательная функция является убывающей и данное неравенство равносильно f(x)-g(x) то есть
Теорема доказана.
Рассмотрим применение данной теоремы при решении примеров.
Пример 1: Решить неравенство:
(две третьих в степени три икс плюс шесть больше четырех девятых)
Приведем правую часть неравенства к основанию две третьих
Так как основание меньше единицы, то данное неравенство равносильно неравенству противоположного смысла , а именно +6,
Т.к. +6,
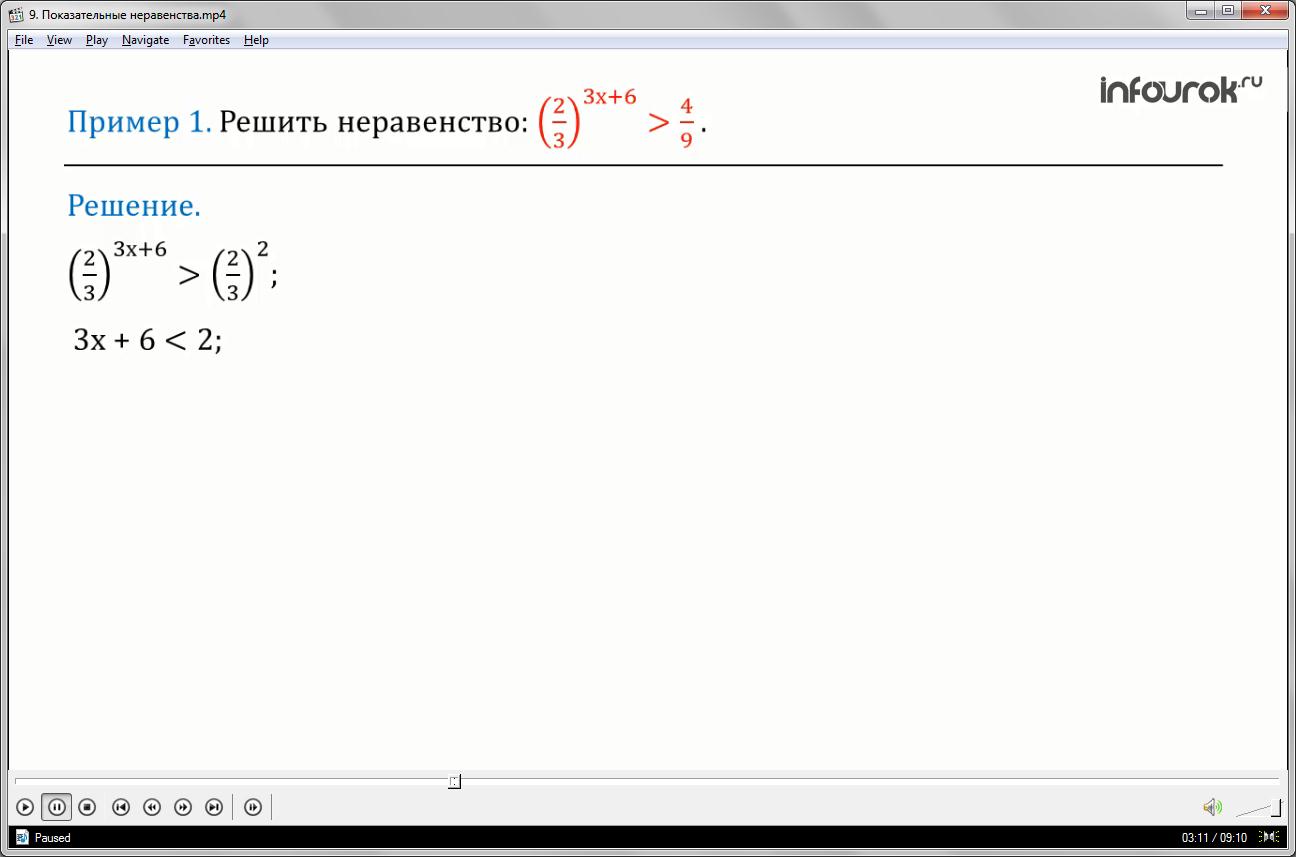
решим полученное неравенство.
Множество решений неравенства состоит из чисел, меньших . Это множество представляет собой числовой промежуток (от минус бесконечности до минус четырех третьих), изображенный на рисунке (ЛИСТ).
Пример 2: Решить неравенство: (два корней из двух, умноженное на два в степени икс минус три больше либо равно одной второй).
Приведем обе части неравенства к основанию два (воспользовавшись определением отрицательной степени:, имеем ; а дальше так как = и по свойству степеней при умножении степеней их показатели складываются.
Так как основание больше единицы, то данное неравенство равносильно неравенству того же смысла:
Т.к.
Решим полученное неравенство
Множество решений неравенства состоит из чисел, больших либо равных . Это множество представляет собой числовой промежуток луч от нуля целых пяти десятых до плюс бесконечности, изображенный на рисунке.
Ответ .
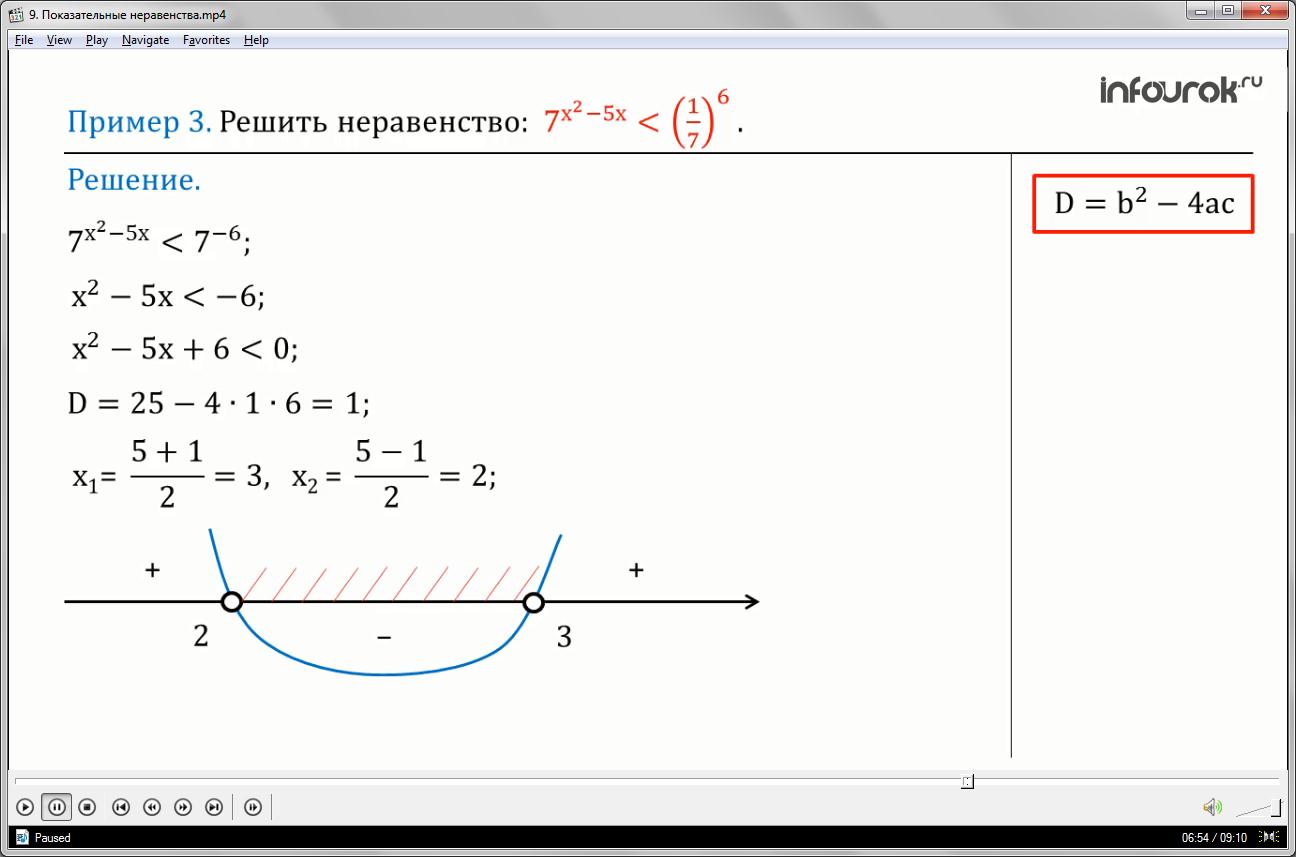
Пример 3: Решите неравенство: (семь в степени икс квадрат минус пять икс меньше одной седьмой в шестой степени).
Приведем обе части неравенства к основанию семь .
Так как основание больше единицы, то данное неравенство равносильно неравенству того же смысла
Корни квадратного трехчлена найдем по формулам:
(икс первый равен минус бэ плюс корень из дэ, деленное на два а;
икс второй равен минус бэ минус корень из дэ, деленное на два а).
Применим метод интервалов. Для этого изобразим схематически параболу (ветви которой направлены вверх, т.к. а = 1) и, с учетом знака неравенства, запишем ответ (рис1) (интервал от двух до трех).
Пример 4: Решить уравнение (три в степени два икс минус четыре, умноженное на три в степени икс, плюс три меньше либо равно нулю).
Введем новую переменную и обозначим (три в степени икс через игрек) и получим квадратное неравенство (игрек квадрат минус четыре икс плюс три меньше либо равно нулю), решим полученное неравенство.
Найдем корни полученного квадратного трехчлена, используя формулу дискриминанта (в нашем случае = - 4, а = 1, с = 3), имеем
Корни квадратного трехчлена найдем по формулам:
Применим метод интервалов. Для этого изобразим схематически параболу (ветви которой направлены вверх, т.к. а = 1 ) и, с учетом знака неравенства, запишем ответ (рис2) (интервал от единицы до трех).
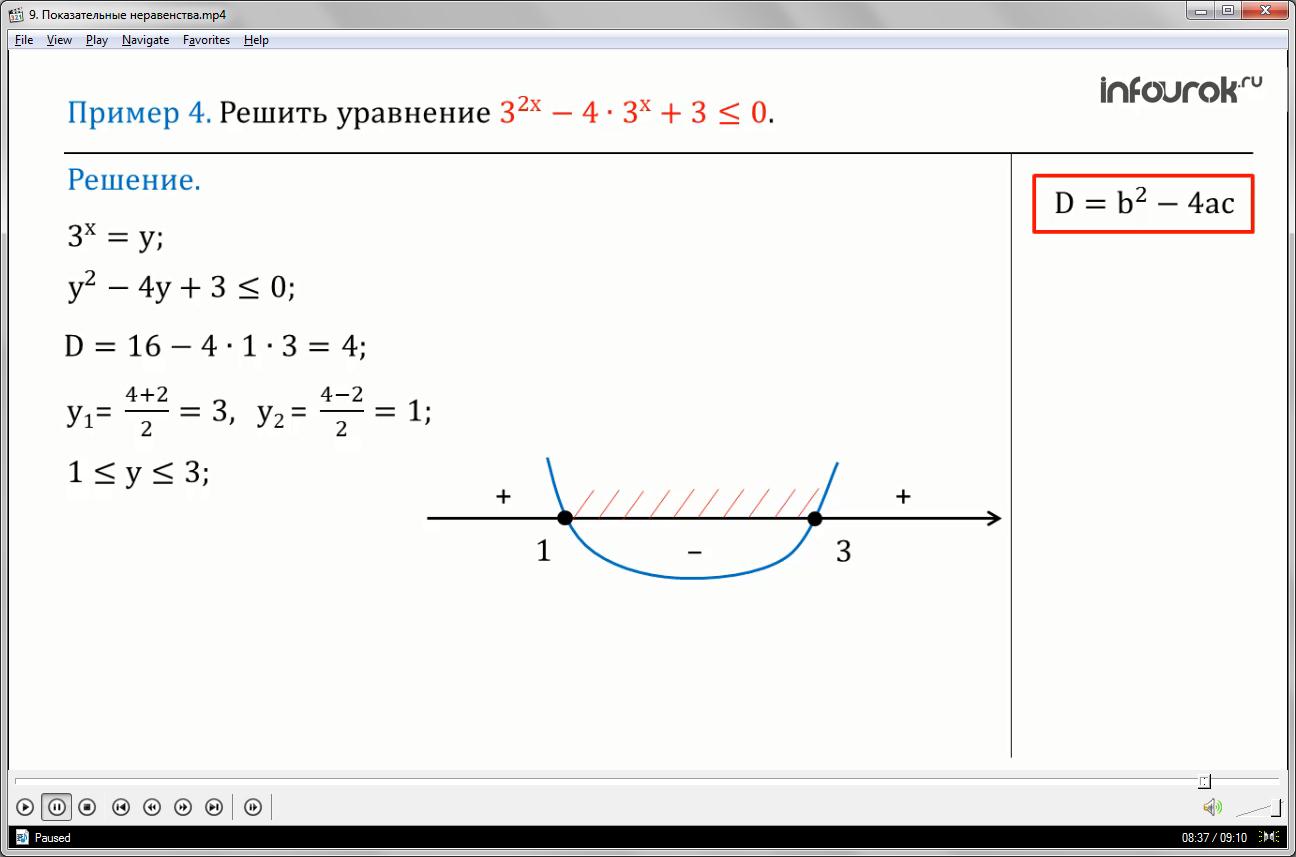
Проведем обратную замену и решим двойное неравенство:
Ответ: 0 (отрезок от нуля до единицы).
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5050 |
| Номер материала | 1058 |