
Урок «Показательные уравнения»

Краткое описание документа:
Дадим определение показательного уравнения.
Показательным уравнением называют уравнения вида (а в степени эф от икс равно а в степени же от икс), где а – положительное число, отличное от единицы, и уравнения, сводящиеся к этому виду.
Вспомним теоремы, изученные на предыдущем уроке.
Терема 1: Если справедливо тогда и только тогда, когда m=n.
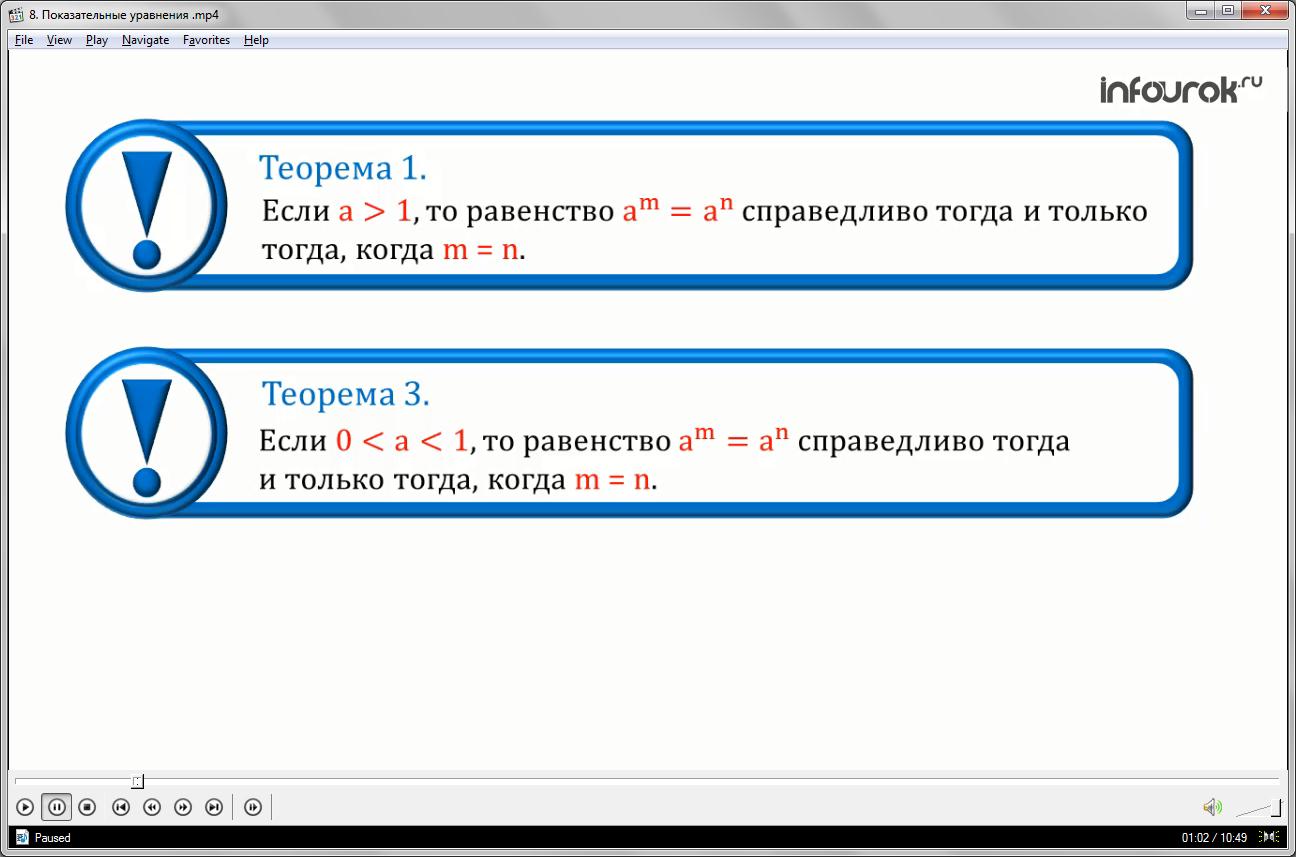
Теорема 3: Если справедливо тогда и только тогда, когда m=n.
Согласно этим теоремам , где , справедливо тогда и только тогда, когда m=n, следовательно, можно сформулировать следующую теорему:
Теорема: Показательное уравнение (а в степени эф от икс равно а в степени же от икс) (где ) равносильно уравнению f(x)=g(x) (эф от икс равно же от икс).
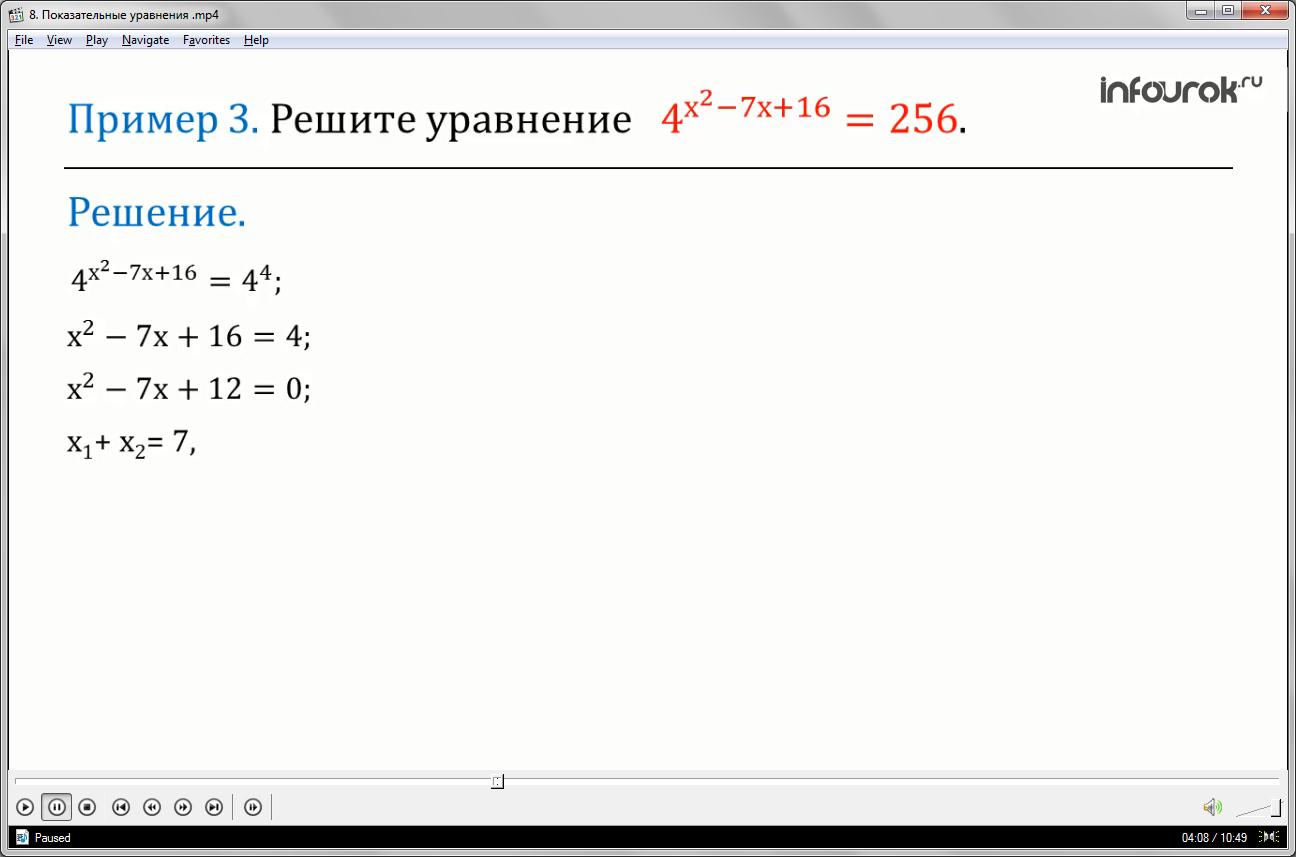
Пример 4: решите уравнение
Применим свойство степени:
вынесем общий множитель за скобки:
решим полученное уравнение
Пример 6: решите уравнение (четыре в степени икс плюс два в степени икс плюс один равно восьмидесяти).
Применим свойство степени и представим
Тогда получим уравнение ,
введем новую переменную, обозначив (два в степени икс через игрек), получим квадратное уравнение ,
применив теорему Виета (произведение корней приведенного квадратного уравнения равно свободному члену, а сумма корней равна второму коэффициенту взятому с противоположным знаком).То есть
у1 + у2 = -2, а у1∙ у2 = -80. Значит, .
Вернемся к обратной замене и решим два уравнения -10
Второе уравнение не имеет решения, так как (два в степени икс всегда положительно), значит, решаем первое уравнение:
,
то есть х=3.
Проанализировав приведенные примеры, данного и предыдущего уроков, можно заметить три приема решения показательных уравнений:
1.Функционально-графический, при котором используются графики функций или их свойства.
2. Уравнивания показателей, при котором применяются свойства степени и теоремы.
3. Введение новой переменной.

Рассмотрим более сложные примеры, где необходимо применять в совокупности различные ранее полученные знания.
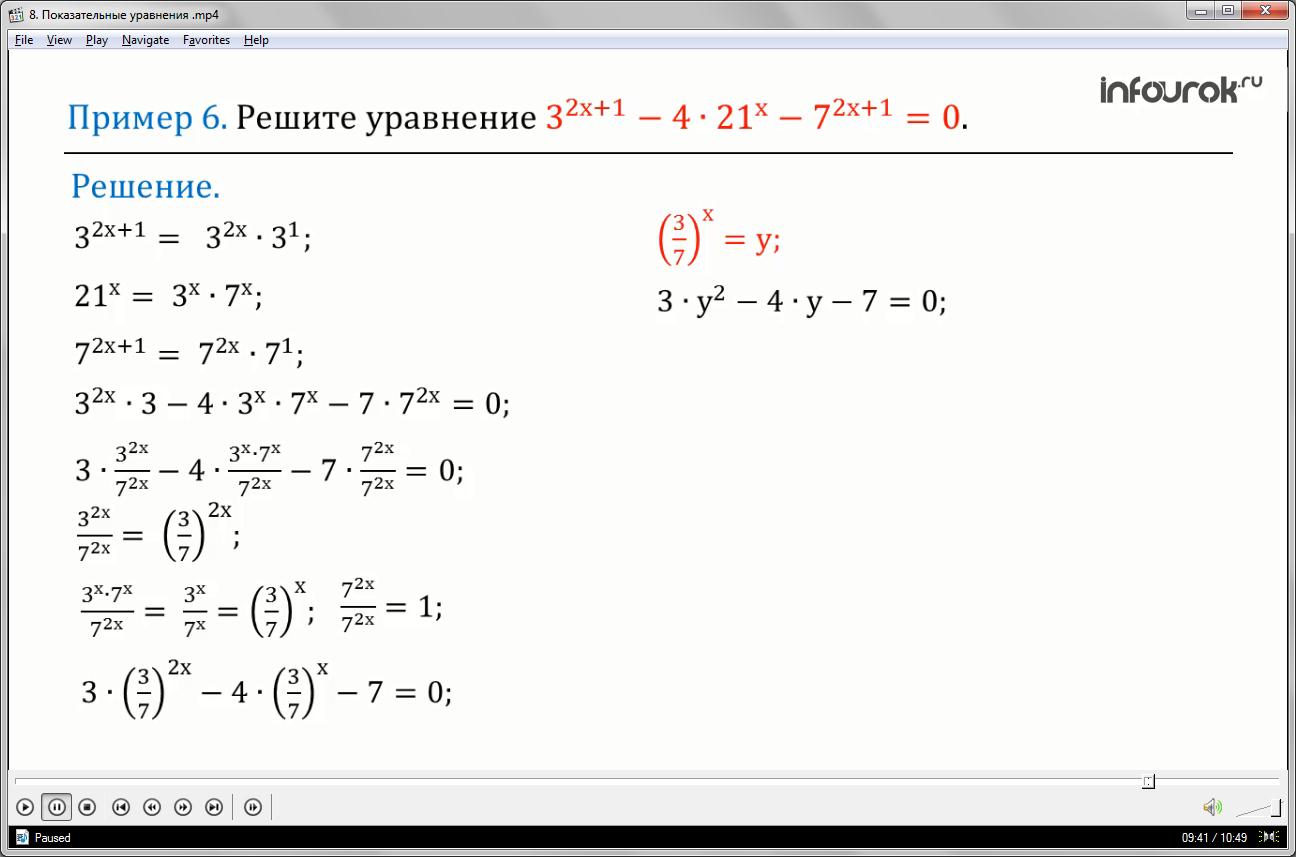
Пример 7: решите уравнение (три в степени два икс плюс один минус четыре, умноженное на двадцать один в степени икс, минус семь в степени два икс плюс один равно нулю).
Далее, используя свойство степени (частное степеней равно степени частному), имеем ; сократив на и применив то же свойство степени.
Следовательно, уравнение имеет вид:
Введем новую переменную и решим полученное уравнение
Используя формулу дискриминанта (в нашем случае
b= -4, a = 3 , c = -7)
Корни квадратного уравнения находятся по формуле:
Вернемся к обозначению и решим два уравнения .
Первое уравнение не имеет решения, так как три седьмых в степени икс всегда положительно), а корнем второго является число минус один, х=-1.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5726 |
| Номер материала | 1057 |