
Урок "Понятие движения"

Краткое описание документа:
Видеоурок«Понятие движения»предназначен для демонстрации учебного материала по соответствующей теме. Движение - важное понятие, понимание которого необходимо для анализа преобразований, решения геометрических задач. В течение демонстрации понятие движения рассматривается, взяв пример осевой симметрии, доказывается теорема о движении некоторого отрезка, следствия из нее. Задача видеоурока – сформировать у учеников представление о движении, его особенностях, облегчить усвоение темы с помощью наглядной демонстрации, способствовать запоминанию учебного материала.

Формирование понимания изучаемых понятий у учеников производится при помощи специальных приемов, которые могут применяться в видео. Для выполнения построений, приближенных к традиционным операциям, которые осуществляются на бумаге или на доске, используется анимация. Также при помощи анимации легче всего представить движение, преобразования. Чтобы учебный материал легче запоминался, формулировки, выводы, определения выделяются цветом и озвучиваются. Чтобы сформировать понимание предмета изучения, важные детали при описании примеров, в построениях также выделяются цветом, делаются соответствующие комментарии.

Видеоурок начинается с представления названия темы и ознакомлением учеников с важным свойством осевой симметрии. Озвучивается свойство, заключающееся в сохранении расстояний при отображении на саму себя плоскости. Пояснение данного свойства осуществляется на примере, рассмотренном в видео. Строятся две точки – M и N, а также прямая а, которая служит осью симметрии. Строятся симметричные точки N1, М1 относительно данной прямой. Симметричность точки М1 точке М означает, что она лежат на прямой, проведенной через точку М и расположенной перпендикулярно оси а. Расстояние от М1 до прямой а, расстояние от точки М до прямой а равняется расстоянию от точки М1 до прямой а. Из точек N и N1проводится перпендикуляр к прямой, соединяющей точку М с М1. При этом образуются точки Р и Р1, в которых перпендикуляры пересекаются с прямой ММ1. При соединении точек Р, M и N, также точек Р, М1 и N1 образуются треугольникиΔMNР и ΔМ1N1Р1. Это прямоугольные треугольники, имеющие одинаковые катеты NР=N1Р1, а также MР=М1Р1. Этих данных достаточно, чтобы утверждать, что треугольники ΔMNР и ΔМ1N1Р1 равны. В равных треугольниках их гипотенузы также равны MN=М1N1. А это означает, что расстояние MN равняется расстоянию между симметричной парой М1 и N1.Отмечается, что анализируя расположение любых других точек, а также симметричных им, ученики могут сами убедиться, что для любых точек данное свойство будет сохраняться справедливым.
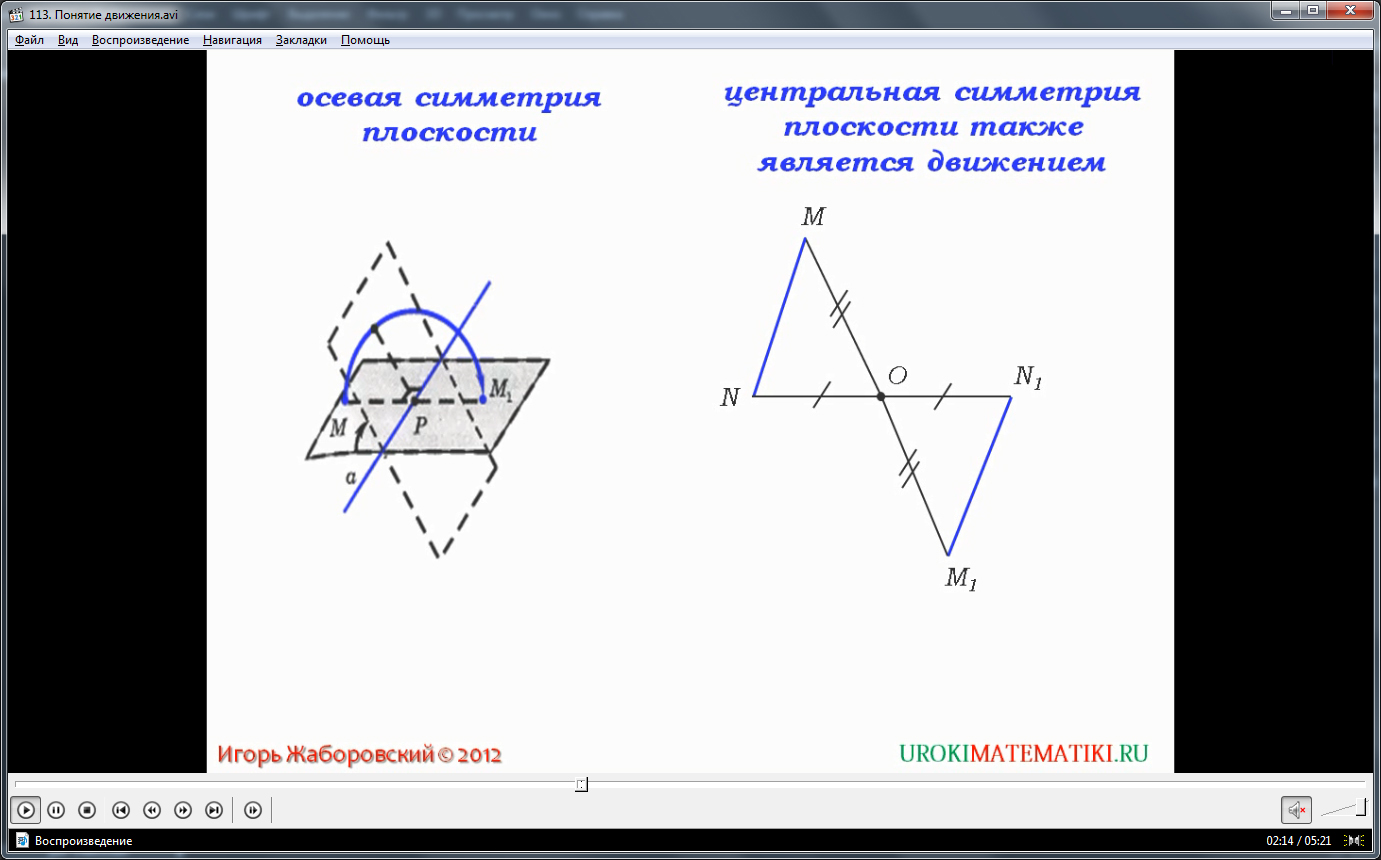
На экране демонстрируется вывод о том, осевая симметрия - отображение, сохраняющее расстояния. Также отмечается, что осевая симметрия, подобно другим видам отображений, обладающих рассмотренным свойством, является видом движения. Далее ученикам предлагается запомнить определение движения, которое сформулировано на экране и озвучивается диктором. В нем указано, что движение плоскости является сохраняющим расстояния отображением на саму себя данной плоскости. Также предлагается, взяв пример осевой симметрии, рассмотреть, почему отображение плоскости с сохранением расстояний называется движением. Для этого на рисунке демонстрируется, как проведенную операцию осевой симметрии можно представить поворотом плоскости в пространстве на 180° вокруг прямой симметрии. На рисунке представлено, каким образом можно доказать справедливость утверждения - центральная симметрия есть движение. Отмечено равенство расстояний, сохраняющееся при симметрии относительно центра – образуя равные треугольники из симметрично отраженных точек, можно отметить и равенство расстояний между этими точками.
Далее рассматривается доказательство утверждения, что отрезок при движении полностью отображается на отрезок. Для этого на экране строится отрезок MN, а также равный отрезок M1N1. Указывается, что можно доказать – если при движении М переходит в М1, а точка N - в точку N1, то весь отрезок MN отображается в отрезокM1N1.В ходе доказательства на первом отрезке MN отмечается точка Р. Она отображается в Р1. Замечено, что МР+PN=MN. Так как известно, что при движении остаются неизменными расстояния, то также являются верными равенства MN=M1N1, М1Р1=МР, N1Р1=NР. При подстановке значений из данных равенств получаем верное равенство М1Р1+N1Р1=M1N1.Следовательно, точка Р1 принадлежит отрезку M1N1.Если такое утверждение было бы неверным, то справедливым было бы неравенство М1Р1+N1Р1>M1N1. Таким же образом доказывается, что во всякую точку отрезка MN отображается какая-либо точка отрезка M1N1. Так как уже доказано, что точка на MN отображается в определенную точку, принадлежащую отрезку M1N1, используя те же равенства, что указаны выше, доказывается, что отображение точки Р1 принадлежит MN.
Демонстрируется следствие из доказанной теоремы. В нем утверждается, что при движении всякий треугольник будет отображаться на равный ему. На рисунке демонстрируются два равных треугольника и направление движения при отображении фигуры. Отмечается, так как все расстояния сохраняются при движении, значит, длины сторон треугольников также одинаковы. А это означает, что треугольники являются равными. Указывается, что также из доказанной теоремы следует, что при движении выполняется отображение прямой в прямую, а угла – в равный угол, луча - в луч.

Видеоурок«Понятие движения» применяется для оптимизации использования учебного времени, повышения эффективности традиционного урока геометрии. Также данный материал рекомендуется к самостоятельному изучению школьниками, которые обучаются на дому или требуют дополнительных занятий для улучшения достижений в учебе. Видеоматериал может стать инструментом дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4897 |
| Номер материала | 746 |