
Урок «Понятие корня n-й степени из действительного числа»

Краткое описание документа:
Решим графически уравнение (икс в шестой степени равно единице), для этого построим в одной системе координат следующие графики функций: ( игрек равен икс в шестой степени)
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
64 |
1 |
0 |
1 |
64 |
и у=1( игрек равен единице). Как мы видим, они пересекаются в двух точках М и Н, где абсциссы точек пересечения являются корнями уравнения (икс в шестой степени равно единице), т.е. . (рис.1)
Найдем корни уравнения.
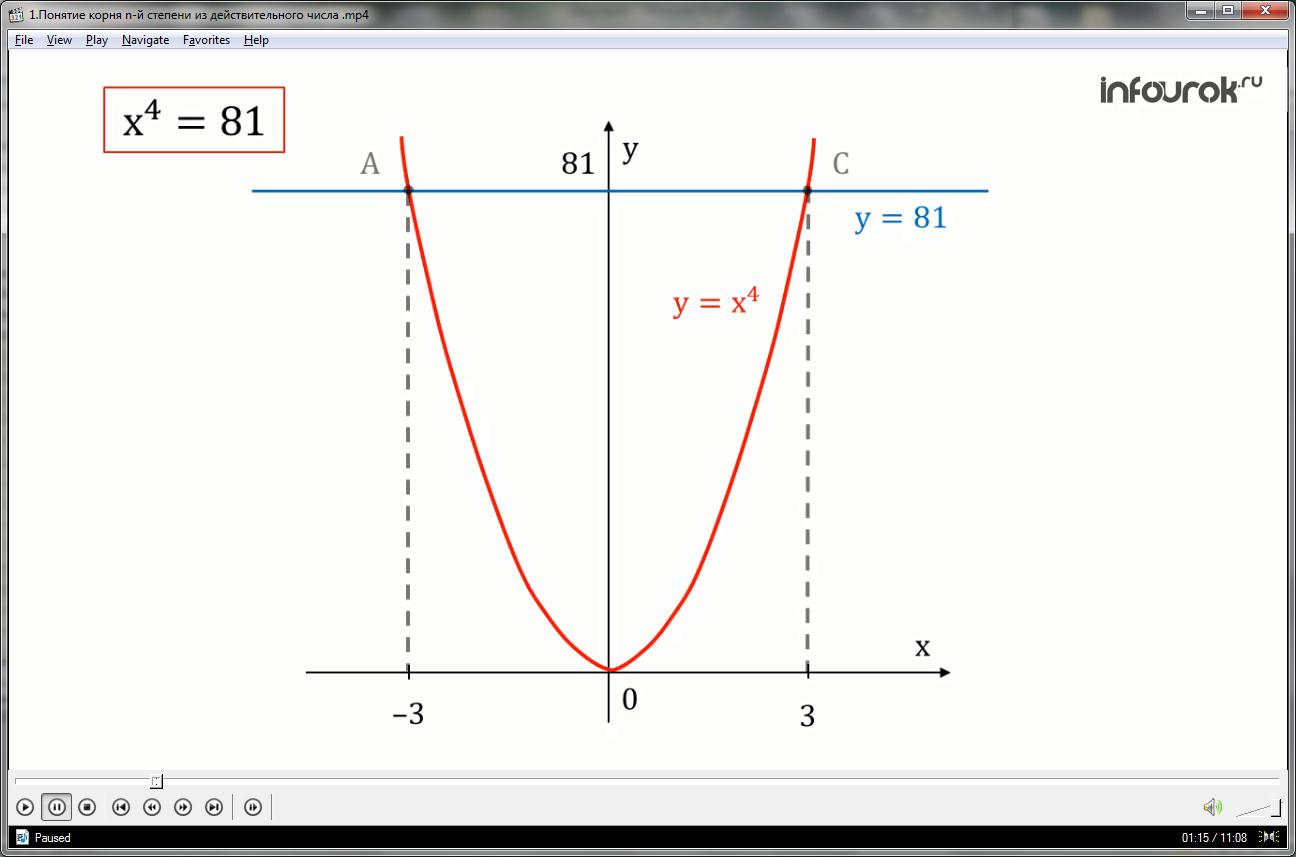
Аналогично строим в одной системе координат графики функции и у=81
|
х |
-3 |
-1 |
0 |
1 |
3 |
|
у |
81 |
1 |
0 |
1 |
81 |
Как мы видим, они пересекаются в двух точках А и С, где абсциссы точек пересечения являются корнями уравнения ,т.е. .(рис.2)
Из решения двух уравнениий мы видим, что каждое из них имеет два корня, причем эти числа взаимно противоположны.
В этих двух уравнениях корни находятся достаточно легко.
Рассмотрим уравнение 7 (икс в шестой степени равен семи) (рис.3)
Строим в одной системе координат графики функции и у=7
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
64 |
1 |
0 |
1 |
64 |
По чертежу видно, что уравнение имеет два корня икс один и икс два, но точные их значения указать нельзя, а только приближенные: они располагаются на оси х, один корень чуть левее точки -1, а второй — чуть правее точки 1.
Для того, чтобы разрешить аналогичные ситуации, математики ввели новый символ , корень шестой степени. И с помощью этого символа корни данного уравнения можно записать так: (икс один равен корень шестой степени из семи и икс два равен минус корень шестой степени из семи).
Рассмотрим решение уравнений с нечетной степенью
и (рис.4)
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
-8 |
-1 |
0 |
1 |
8 |
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
-32 |
-1 |
0 |
1 |
32 |
Как видно из чертежей, каждое из уравнений имеет один корень, но в первом уравнении корнем является целое число два, а во втором точно указать значение нельзя, следовательно, для него введем обозначение (корень пятой степени из шести).
Исходя из рассмотренных примеров сделаем вывод и дадим определение:
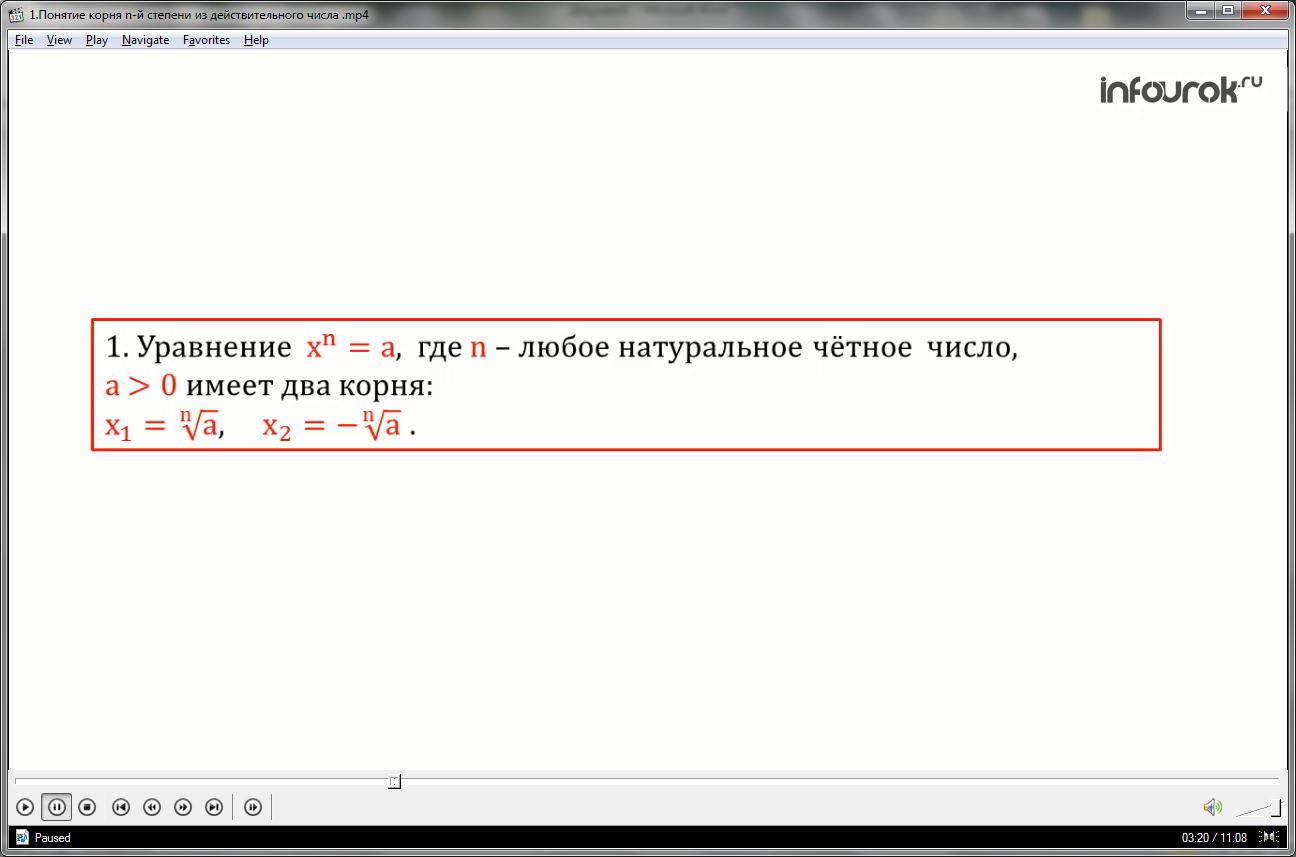
1.Уравнение (икс в степени эн равно а) , где n(эн) – любое натуральное четное число, а имеет два корня:
(корень энной степени из числа а и минус корень энной степени из числа а)
2.Уравнение (икс в степени эн равно а) , где n(эн) – любое натуральное нечетное число, а (а больше нуля) имеет один корень: (корень энной степени из числа а)
3.Уравнение (икс в степени эн равно ноль) имеет единственный корень х=0 (икс равен нулю).
Определение: Корнем n-й (энной) степени из неотрицительного числа а (n=2,3,34,5…) называют такое неотрицительное число ,которое при возведении в степень n (эн) дает в результате число а.
Это число обозначают (корнем энной степени из числа а). Число а при этом называют подкоренным числом, а число n (эн) – показателем корня.
(Частный случай вы изучали в алгебре 8-го класса, когда n=2: пишут (корень квадратный из а)).
Необходимо запомнить, если
.
(если а неотрицательное число, n — натуральное число, большее единицы, то корень энной степени из числа а есть неотрицательное число и если корень энной степени из числа а возвести в энную степень, то получим число а, то есть подкоренное число).
Другими словами, определение можно перефразировать следующим образом:
(корнем энной степени из числа а называется число бэ, энная степень которого равна а).
Под термином извлечение из под корня понимают нахождение корня из неотрицательного числа. Другими словами, нужно выполнить обратное действие к возведению в соответствующую степень. Рассмотрим таблицу:
|
Вазведение в степень |
Извлечение корня |
Будьте внимательны, согласно определению корня энной степени, в таблице рассматриваются только положительные числа.
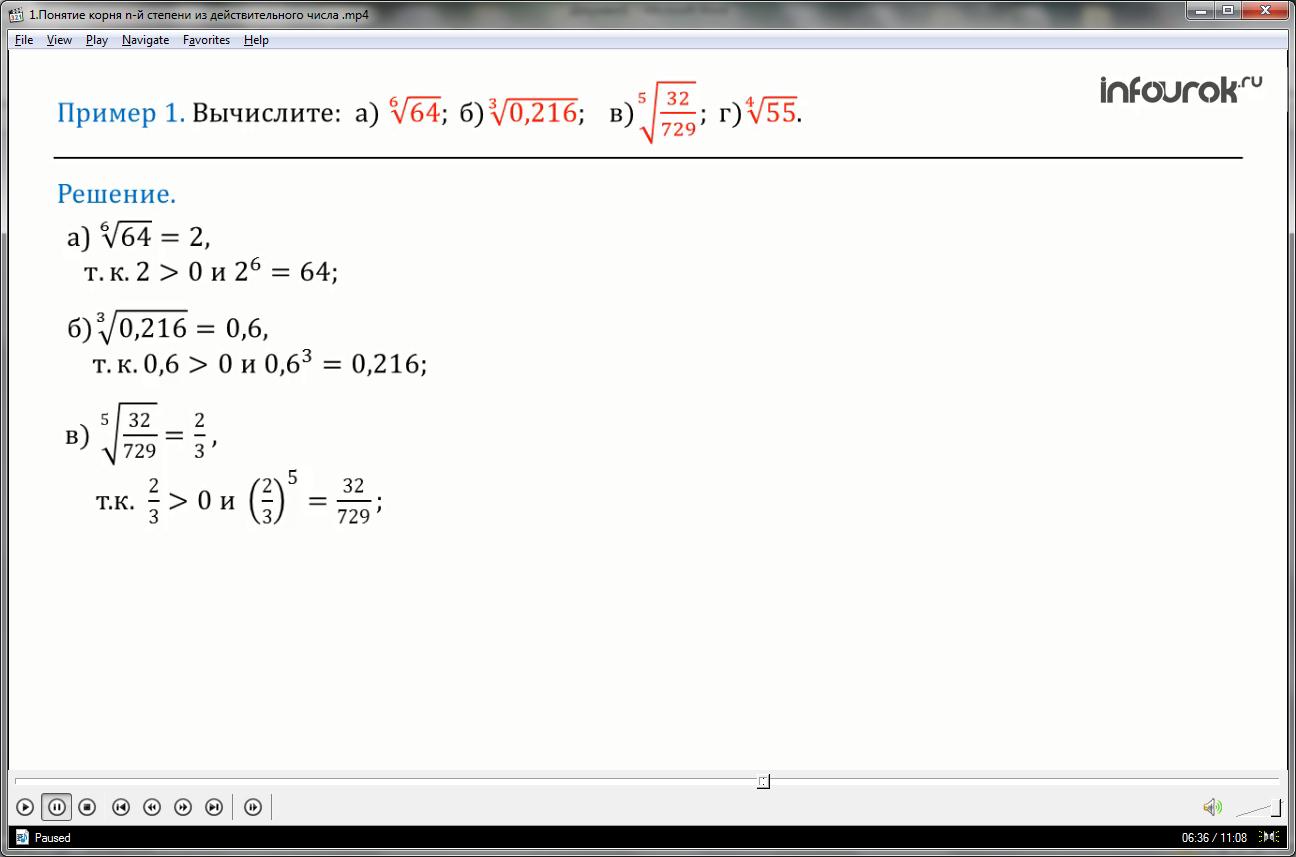
Рассмотрим пример 1: Вычислите
Решение:
а)(корень шестой степени из шестидесяти четырех равен двум, так как два – положительное число и два в шестой степени равно шестидесяти четырем).
(корень третьей степени из ноля целых двести шестнадцати тысячных равен ноль целых шесть десятых, так как найденное число положительно и в третьей степени дает падкоренное число)
,так как =
г) Согласно определению корня энной степени запишем два равенства: и
Следовательно, нам нужно найти число, которое в четвертой степени равно 55, но два в четвертой степени равно шестнадцати, что меньше 55,
, и три в четвертой степени равно восьмидесяти одному, что больше 55, . Значит, точного значения указать нельзя, поэтому воспользуемся знаком приближенного равенства с точностью до сотых .
Для извлечения корня из отрицательного числа пользуются вторым определением:
Определение: Корнем нечетной степениn из отрицательного числа а (n=3,5,7,…)называют такое отрицательное число m, которое, будучи возведено в степень n, дает в результате число а.
число а при этом называют подкоренным числом, а число n (эн) – показателем корня.
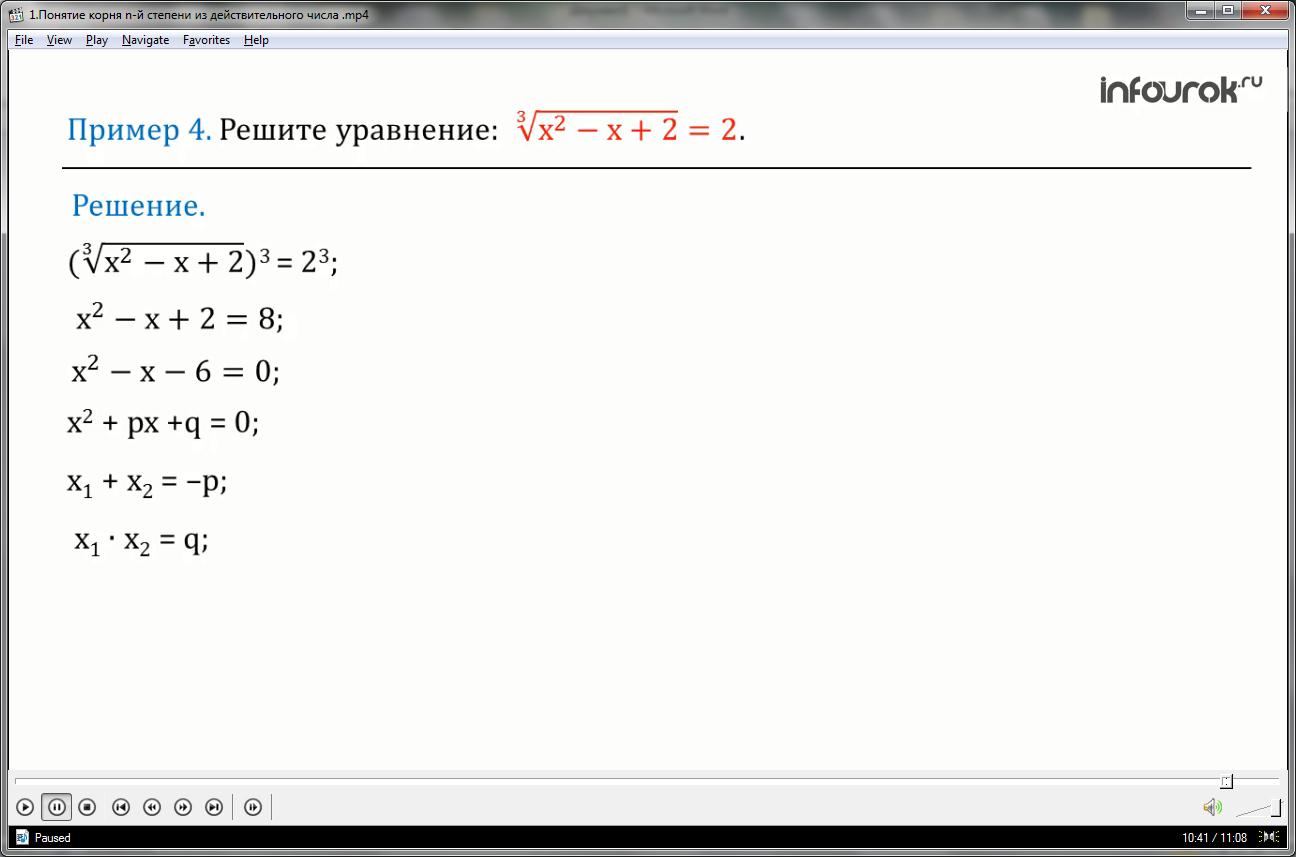
Для корня нечетной степени справедливы два свойства:
если
(если а — отрицательное число,n — натуральное нечетное число, большее единицы, то корень энной степени из числа а есть отрицательное число, и если корень энной степени из числа а возвести в энную степень, то получим число а, то есть подкоренное число).
Проанализировав определения и свойства корня энной степени из числа, сделаем вывод:
- Корень четной степени имеет смысл (то есть определен) только для неотрицательного подкоренного выражения;
- корень нечетной степени имеет смысл для любого подкоренного выражения
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5671 |
| Номер материала | 1050 |