
Урок «Понятие логарифма»

Краткое описание документа:
10. Понятие логарифма
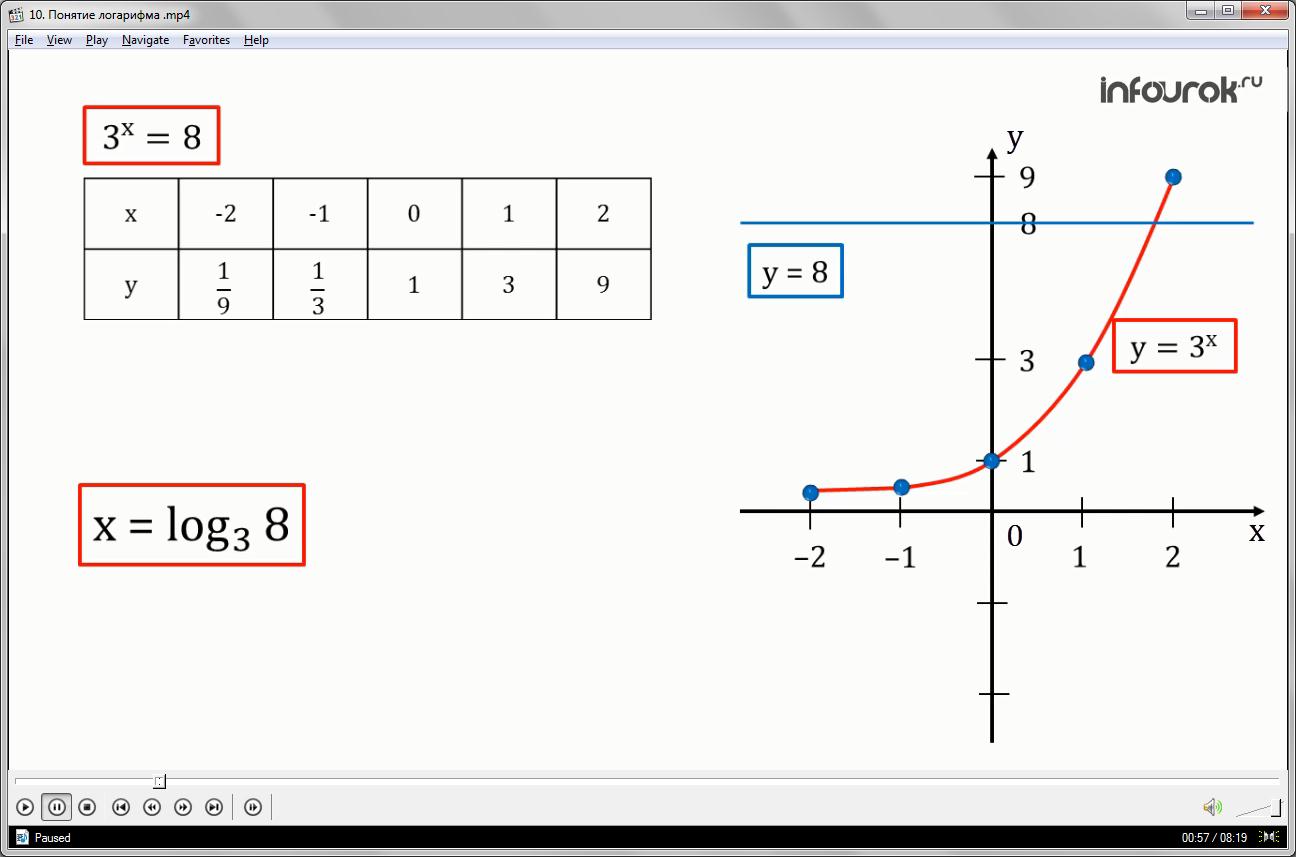
Решим графически уравнение (три в степени икс равно восьми), для этого в одной системе координат построим два графика функции у=8 и у= (Рис 1). Составим таблицу:
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у |
1 |
3 |
9 |
Чертеж показывает, что уравнение имеет один корень, но точного значения указать нельзя. В связи с этим в математике был введен новый символ – логарифм по основанию а. Используя данный символ, можно записать корень уравнения х= (икс равен логарифму восьми по основанию три).
Сейчас для любого уравнения вида
(а в степени икс равняется бэ, где а и бэ — положительные числа и а неравно единице, существует единственный корень — икс равен логарифм числа бэ по основанию а).
Дадим определение понятия логарифма: логарифмом положительного числа b (бэ) по положительному и отличному от единицы основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b (бэ).
Например: (логарифм двадцати семи по основанию три равен трем, так как три в кубе равно двадцати семи).
(логарифм одной шестьдесят четвертой по основанию два равен минус шесть, так как два в минус шестой степени равно одной шестьдесят четвертой).
(логарифм восьмидесяти одного по основанию одной девятой равен минус два, так как одна девятая в минус второй степени равна восьмидесяти одному).
(логарифм четырех по основанию шестнадцати равен одной второй, так как шестнадцать в степени одна вторая равно четырем).
Выделим и обоснуем три формулы:
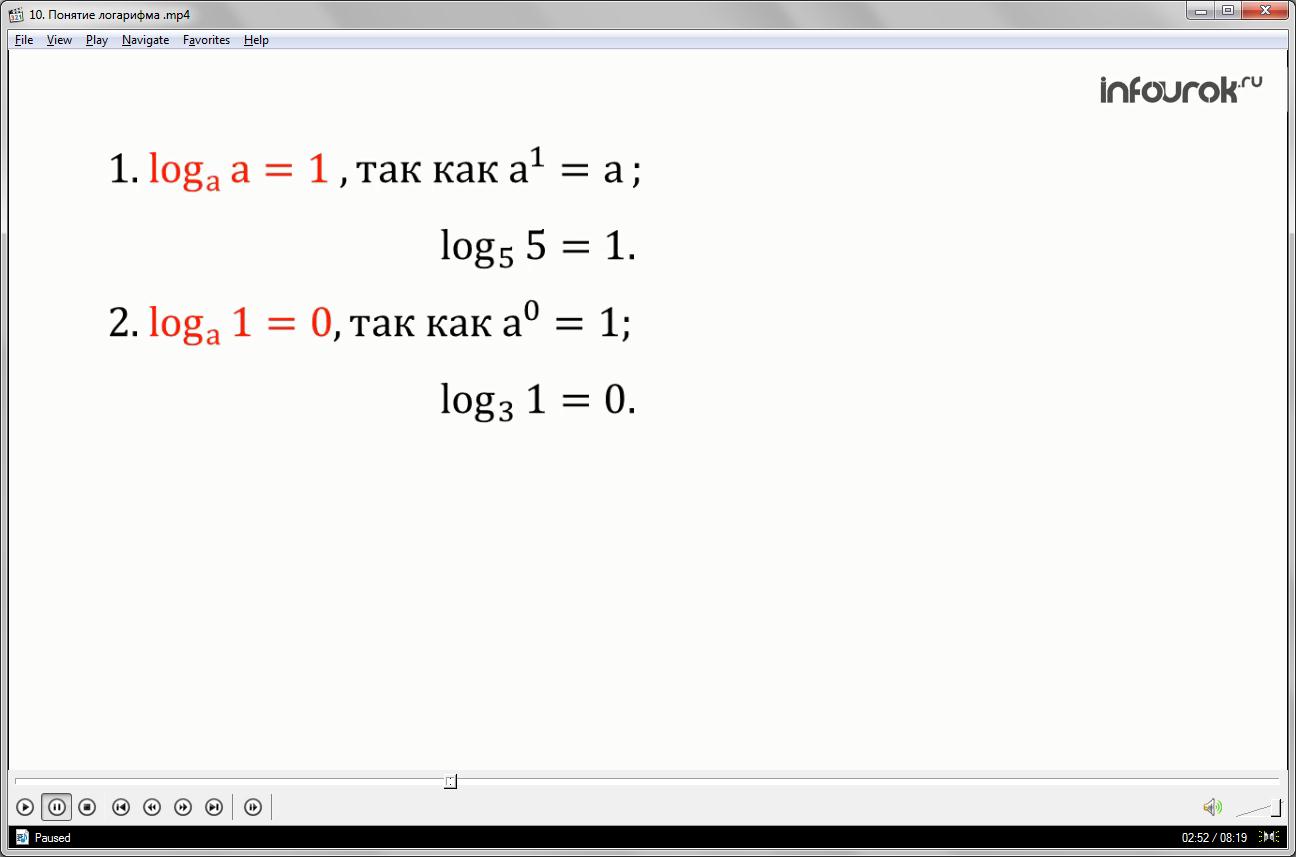
- (логарифм числа а по основанию а равен единице, так как любое число в первой степени равно самому себе). Значит,
- (логарифм единицы по основанию а равен нулю, так как любое число в нулевой степени равно единице). Таким образом,
3. (логарифм числа а в степени эм по основанию а равен эм, так как а в степени эм равняется а в степени эм). Следовательно,
Рассмотрим . Так как точного рационального значения (логарифма восьми по основанию три) мы указать не можем, то такие числа принято называть иррациональными.
Обоснуем это:
Пусть – рациональное число, тогда его можно представить в виде дроби эм, деленное на эн, где эм и эн — натуральные числа: . Тогда, применив определение логарифма и свойство степени, получим (три в степени эм равно восьми в степени эн), но этого быть не может, так как три в степени эм – целое число, кратное трем, а восемь в степени эн – целое число кратное двум
Получили противоречие нашему утверждению, значит
Посмотрите и запомните, как на математическом языке выглядит определение логарифма: (а в степени логарифм числа бэ по основанию а равно бэ)
Например:
Другими словами, если основание степени и основание логарифма, стоящего в степени, равны, то значение выражения равно подлогарифмическому числу.
Рассмотрим вычисление значения логарифма.
Пример1: Вычислите (логарифм числа двести двадцать пять корней кубических из пятнадцати по основанию одна пятнадцатая)
(логарифм числа двести двадцать пять корней кубических из пятнадцати по основанию одна пятнадцатая)
Применим определение логарифма и получим =225 (одна пятнадцатая в степени икс равно двести двадцать пять корней кубических из пятнадцати).
Решим полученное показательное уравнение.
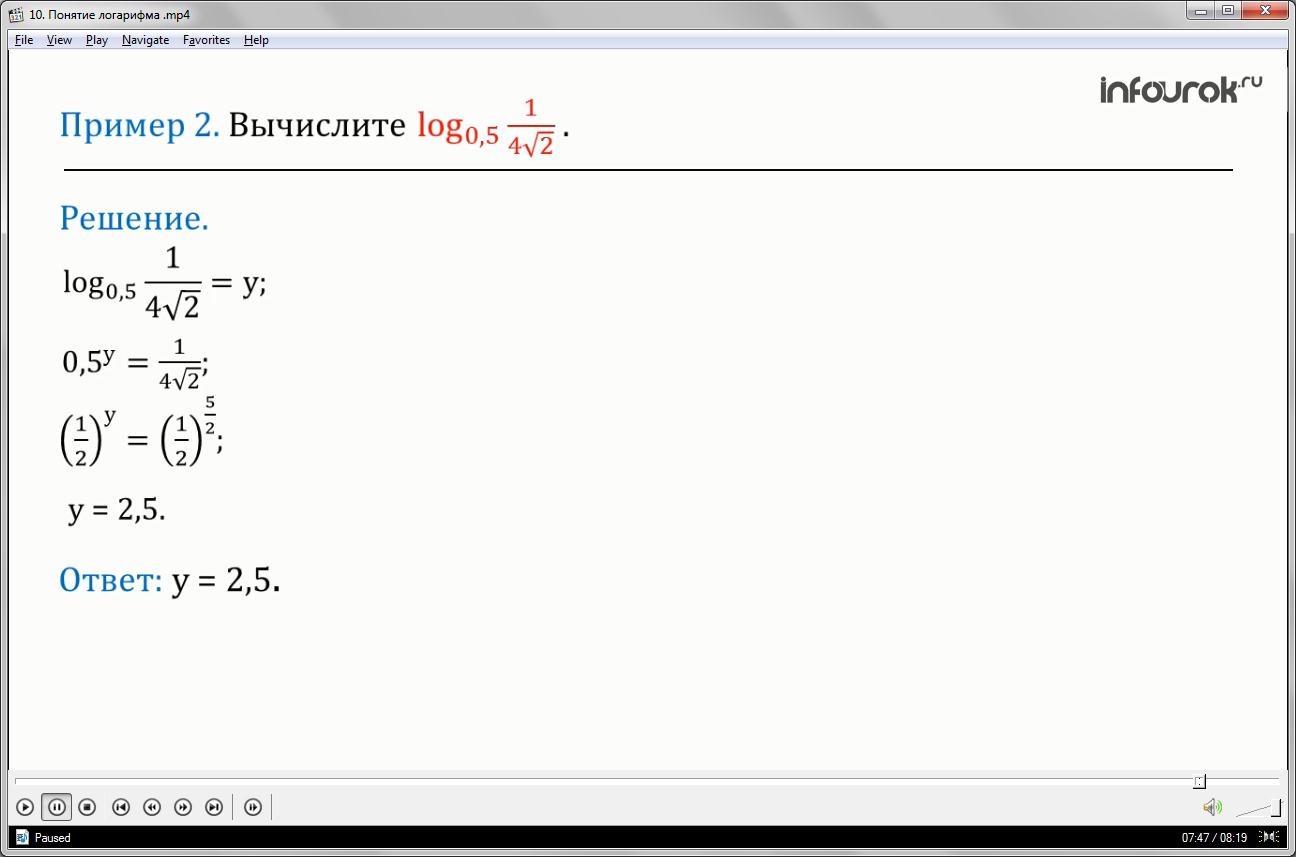
приведя обе части уравнения к основанию пятнадцать получим:
воспользуемся свойством степени (при умножении показатели складываются)
значит, (т.к. )
получим ответ: икс равен минус семь третьих
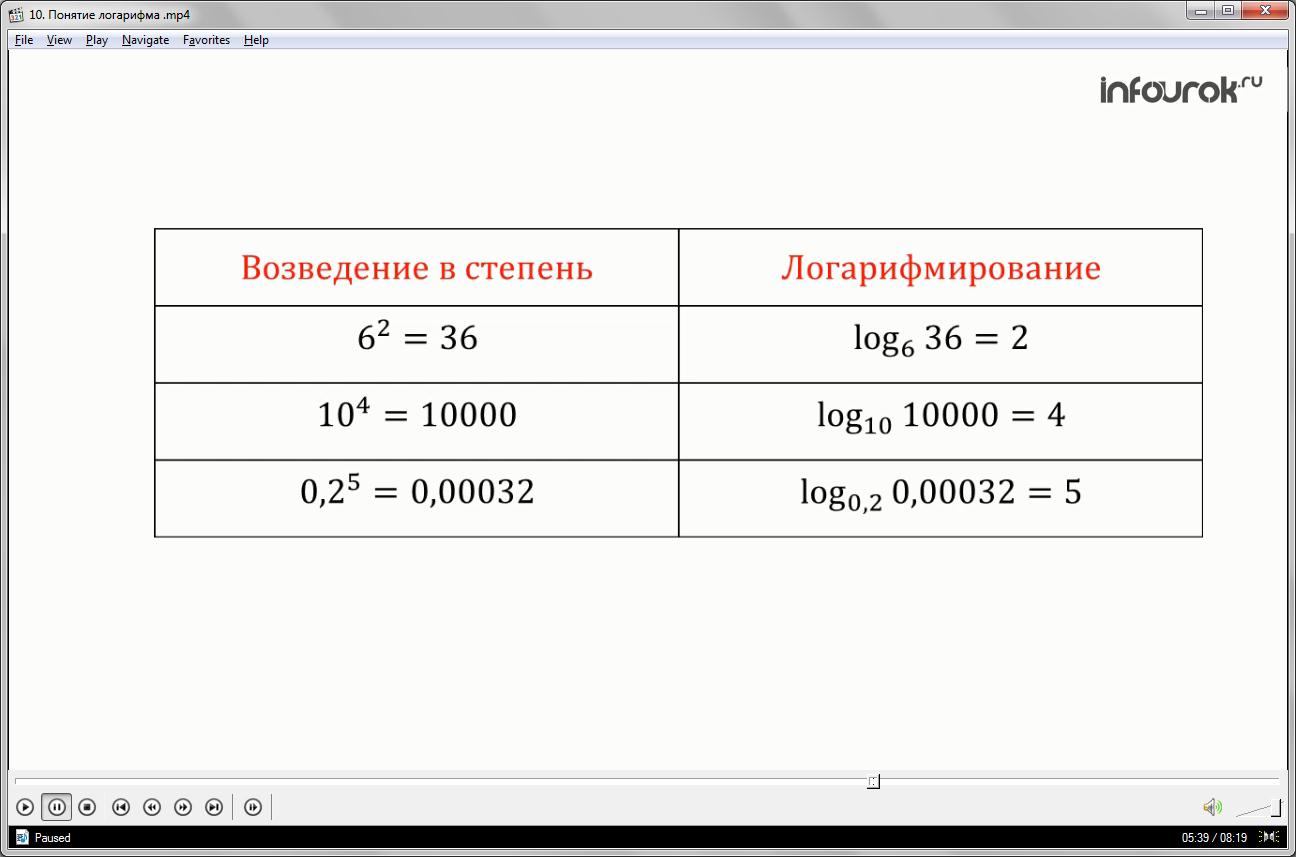
Математики для логарифма по основанию 10 ввели новое обозначение и назвали логарифм по основанию десять десятичным логарифмом. Вместо.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5337 |
| Номер материала | 1059 |