
Урок «Последовательности»

Краткое описание документа:
Видеоурок «Последовательности» содержит видеоматериал для наглядного представления учебного материала по данной теме. В ходе видеоурока вводится понятие последовательности, представляются формулы для расчета некоторого члена последовательности, основные виды последовательностей. Материал может заменить объяснение учителя по теме или помочь учителю представить учебный материал в качестве сопровождающего объяснение наглядного материала.
Для повышения эффективности урока в видеопособии используются анимационные эффекты, важные понятия и детали выделяются рамкой, цветом. Такое представление способствует удержанию внимания учеников на изучаемом материале, лучшему запоминанию материала, усваиванию понятий.
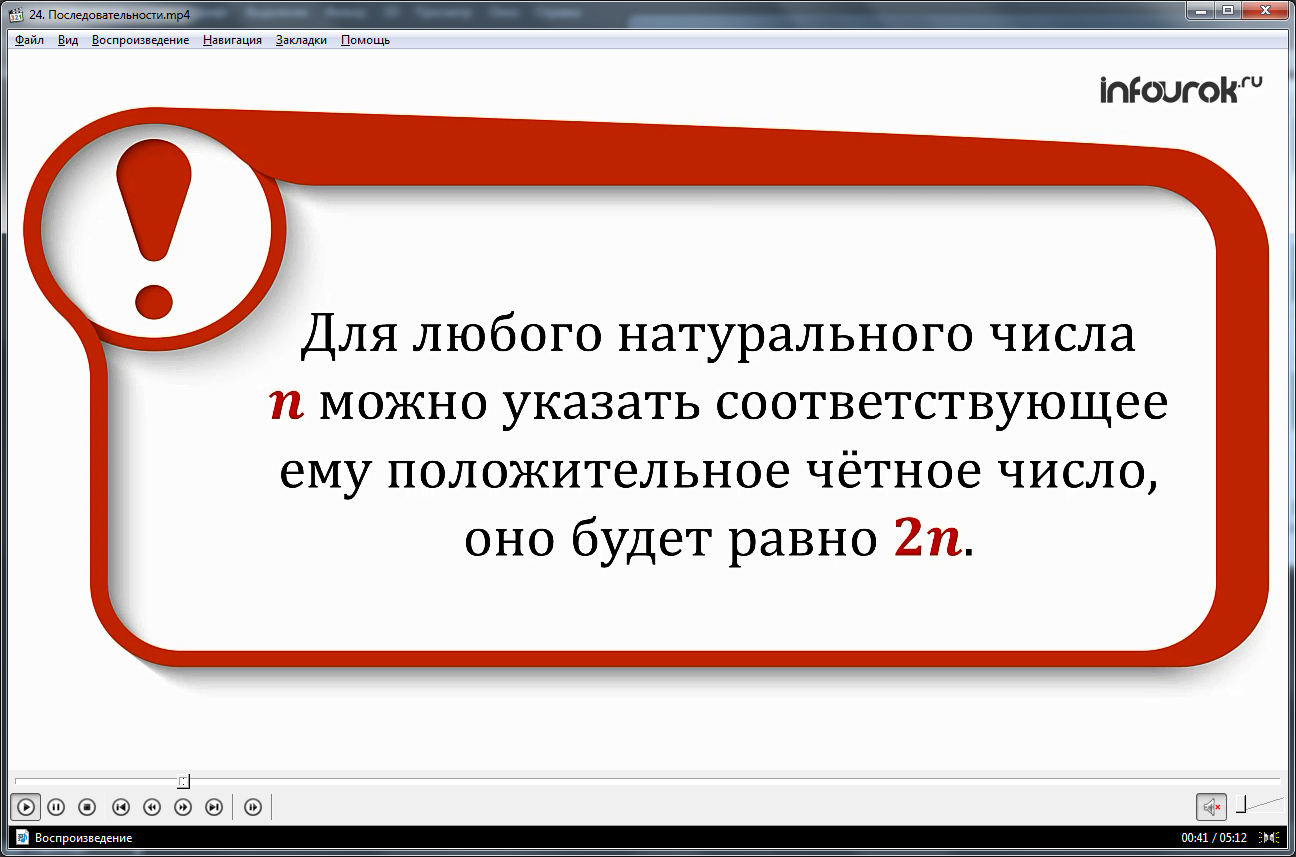
Видеоурок начинается с представления темы и введения понятия последовательности. Предлагается рассмотреть свойства некоторого числового ряда. Его примером служит ряд четных чисел – 2, 4, 6 и т.д. Понятие «последовательность» выделено в рамку на экране для запоминания. Отмечаются особенности данной последовательности, которые заключаются в том, что каждому порядковому номеру члена данной последовательности будет соответствовать положительное четное число 2n.
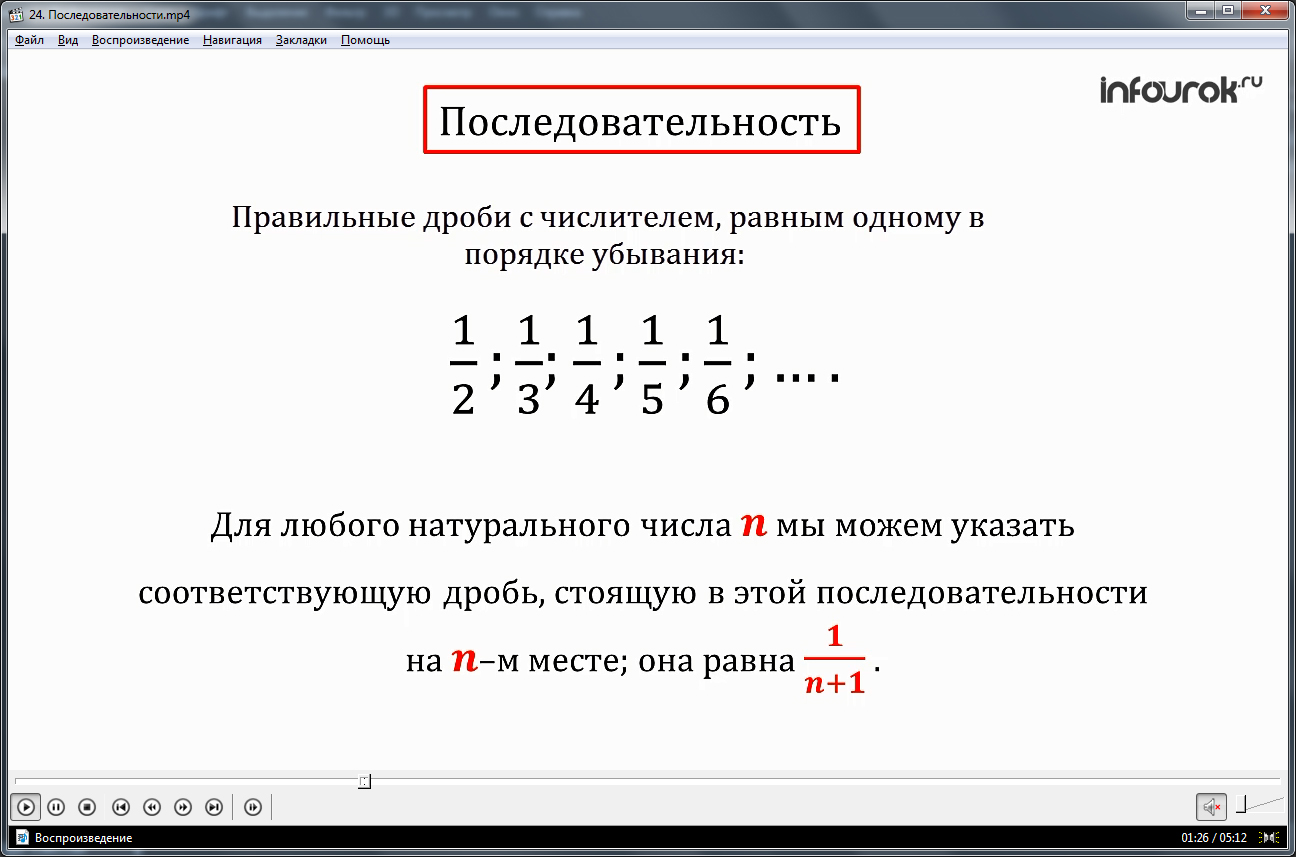
Рассматривается еще одна последовательность, члены которой являются дробными числами, в числителе которых единица, а в знаменателе последовательно идут числа по возрастанию, начиная с двух: ½, 1/3, ¼, 1/5, … Описать данную последовательность можно, отмечая, что каждый член последовательности формируется в соответствии с его порядковым номером n в последовательности и формулой 1/(n+1). В соответствии с указанной закономерностью, можно определить любой последующий член данной последовательности. Указывается, что таким образом на 7-м месте будет стоять 1/8, на 100-м будет располагаться 1/101 и т.д.
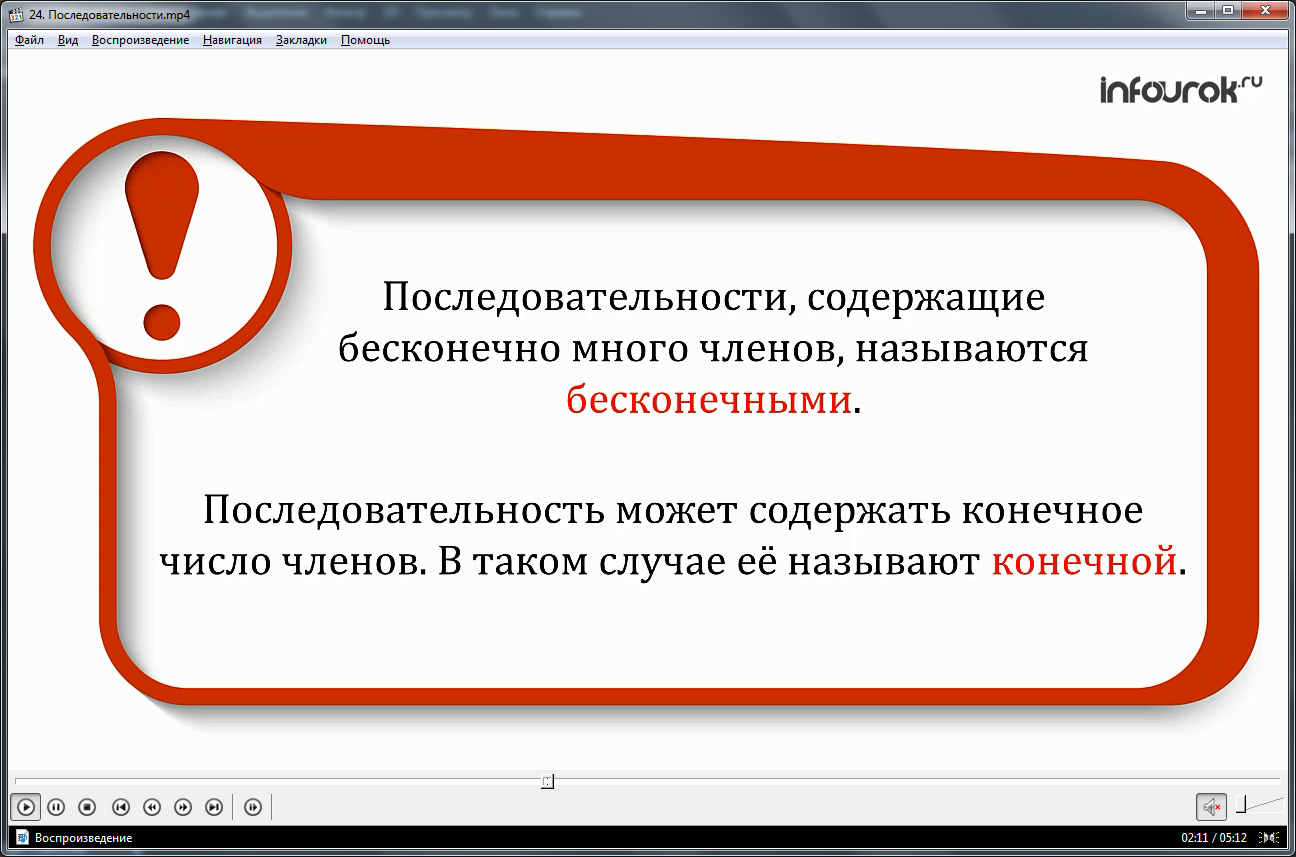
Далее вводится понятие членов последовательности как чисел, образующих данную последовательность. Определение члена последовательности выделено для запоминания в рамке. Указывается математическая запись членов последовательности в виде букв с индексами, которые обозначают порядковый номер – а1, а2, а3… Далее вводится общее обозначение некоторого n-ного члена последовательности an. Также на экран выведено общее обозначение последовательности (an). При этом отмечается, что ранее рассмотренные последовательности не имеют конца, поэтому называются бесконечными последовательностями. Также выделена информация о том, что последовательности могут состоять из конечного числа членов. Такие последовательности называются конечными. Приводится пример конечной последовательности 20, 21, 22, …, 88, 89 и понятие конечной последовательности выделено в рамку для запоминания. Также здесь отмечено, что для задания некоторой последовательности следует указывать способ нахождения некоторого члена последовательности под любым порядковым номером. Примером такого задания является формула n-го члена последовательности. Примером служит формула, по которой можно определить любой член последовательности, рассмотренной в первом примере. То есть последовательность четных чисел задается формулой an=2n. Рассмотренный пример последовательности с дробными числами обозначается формулой некоторого n-го члена последовательности bn=1/(n+1).
Далее описывается пример последовательности, заданной формулой yn=n2-2n. Описано, каким образом формируются члены последовательности, подставляя их порядковый номер в данную формулу. Таким образом получаются значения каждого члена: у1=-1, у2=0, у3=3 и т.д. В результате получаем последовательность чисел -1, 0, 3, -8,…
Второй пример рассматривает формирование знакопеременной последовательности, в которой ее члены формируются по формуле xn=(-1)n·100. В данной последовательности каждый член принимает значение 100 или -100, в зависимости от четности порядкового номера. Соответственно, если порядковый номер четный, то значение xn будет 100 для нечетного - -100. Последовательность будет представлять ряд чисел -100, 100, -100, 100 и т.д.
Третий пример задает последовательность с общим представлением ее члена cn=4. Члены данной последовательности будут х1=4, х2=4, х3=4 и т.д. Сама последовательность выглядит так: 4, 4, 4, …
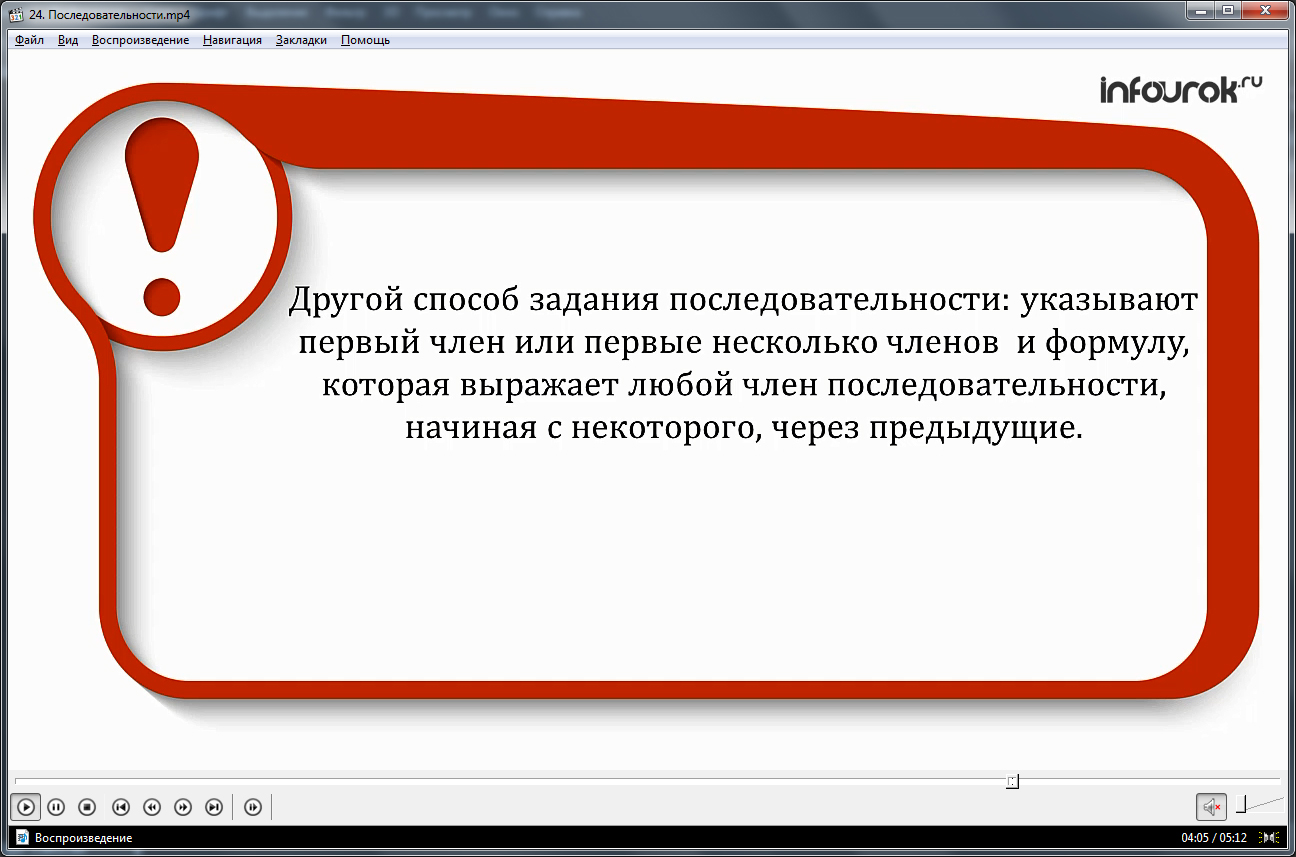
После введения понятия о последовательности и представлении ее формулой общего представления члена последовательности указывается другой способ задания последовательности, который называется рекуррентным. Данный способ состоит в задании последовательности через первый член или несколько членов, а остальную часть – формулой, выражающей правило формирования последующих членов. Такую формулу также называют рекуррентной. Данные понятия выделены для запоминания в рамку, а сами названия обозначены красным цветом.
Последним описывается пример задания последовательности рекуррентным способом. Последовательность (un) определяется с указанием первых ее двух членов u1=1, u2=1 и формулой, в соответствии с которой формируются последующие члены un+1= un+ un-1. Эта формула верна для n>2. Такое описание дает следующую последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. эта последовательность имеет определенную ценность в математике, поэтому ученикам даются некоторые сведения о ее истории. Последовательность была исследована итальянским математиком Леонардо де Пиза, которые более известен под именем Леонардо Фибоначчи, а данная последовательность иначе называется числами Фибоначчи.
Видеоурок «Последовательности» предназначен для использования на уроке алгебры в школе как наглядный материал для повышения эффективности преподавания. Также материал может быть полезен при дистанционном обучении. Рекомендуется использовать этот материал и школьником для самостоятельного рассмотрения и изучения темы.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 12488 |
| Номер материала | 668 |