
Урок «Уравнение с двумя переменными и его график»

Краткое описание документа:
Видеоурок «Уравнение с двумя переменными и его график» знакомит учеников с понятием уравнения с двумя переменными, его решением, дает представление о графике уравнения с двумя переменными, его построении. Задача видеоурока – наглядно представить учебный материал по данной теме, облегчая выполнение задач учителя на уроке и давая возможность ему более эффективно использовать время урока.
Возможности видеоурока больше, чем любого другого наглядного пособия. Возможность использовать анимационные эффекты, заменить учителя в демонстрации построения графиков, чертежей, выполнение голосового сопровождения позволяет повысить эффективность урока, более рационально распределять время, удерживать внимание учеников на изучаемом материале.
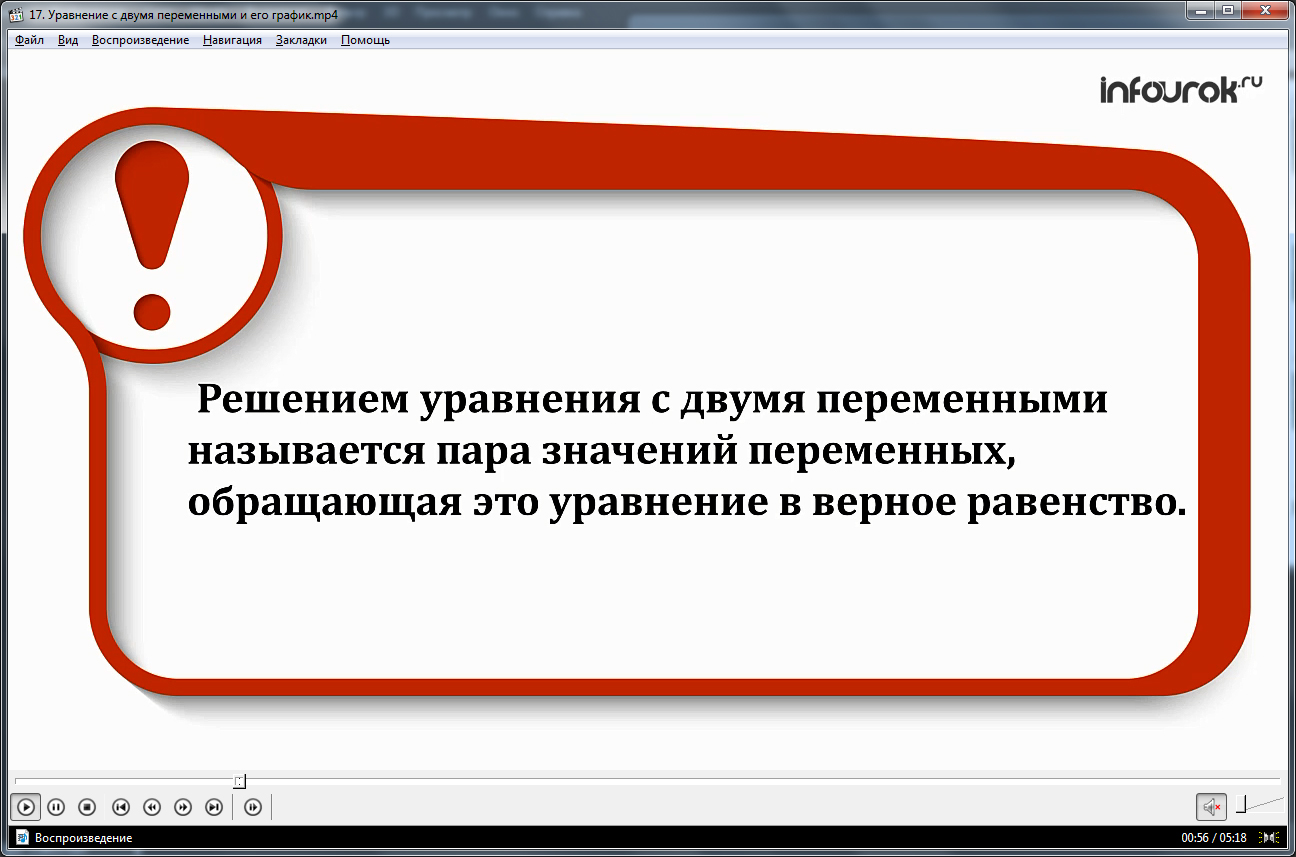
Видеоурок начинается с представления темы. Ученикам представляются примеры уравнений с двумя переменными: 3х+4у=16, х2=9-у2, ху-8=0. Далее дается представление о решениях уравнения с двумя переменными. Демонстрируется подстановка значений переменных х=4 и у=1, которые превращают уравнение 3х+4у=16 в справедливое равенство. После объяснения сути решения уравнения, вводится понятие решения уравнения, которое в данном случае представляет собой пару чисел (4;1), в котором на первом месте представлено значение переменной х, а на втором – значение переменной у. Далее для запоминания учениками на экран выведено определение, что такое решение уравнения, которым называется пара значений для переменных, обращающая уравнение в верное равенство.
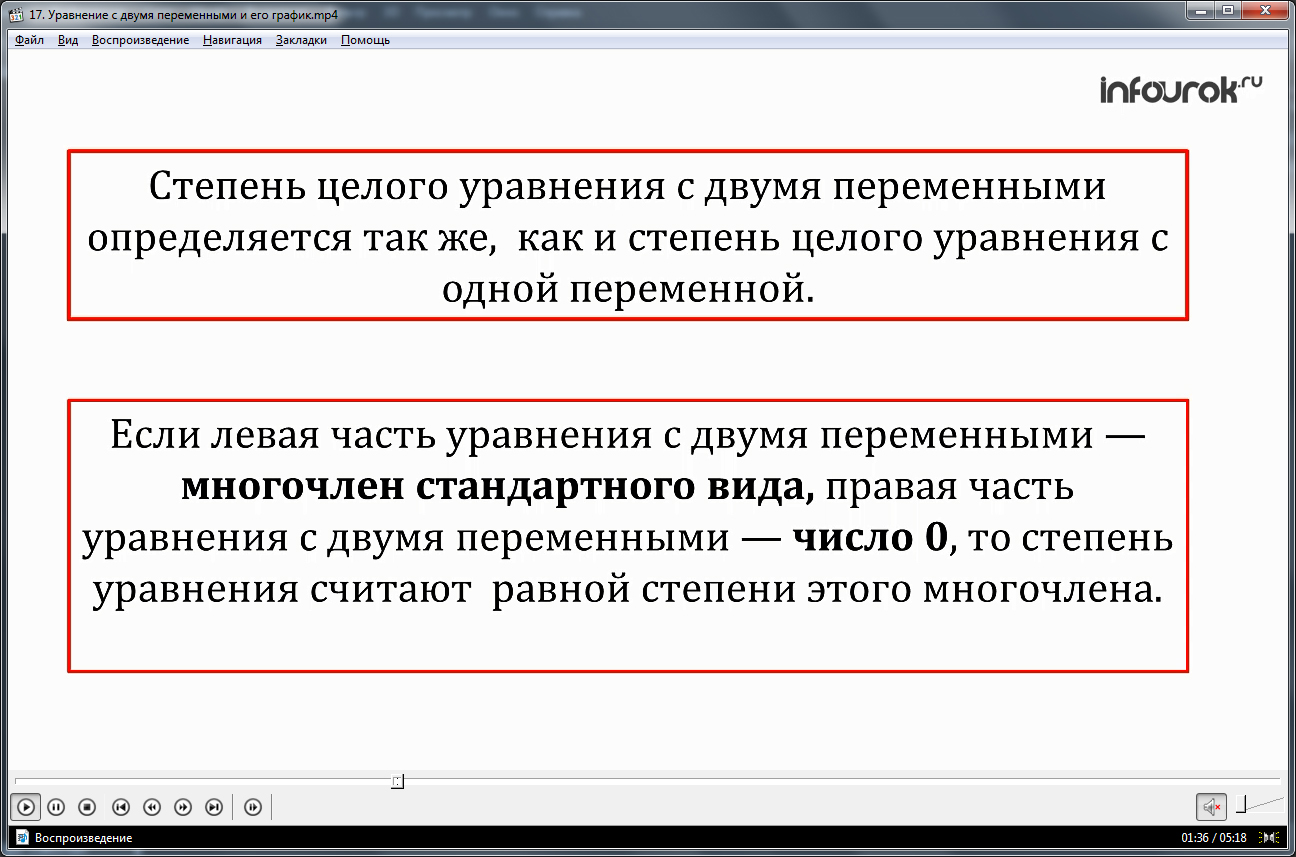
Уточняется особенность уравнения, имеющего две переменные - в большинстве случаев они имеют бесконечное множество решений. Вводится понятие равносильных уравнений, представляющих собой уравнения, имеющие одинаковое множество решений. Отмечается одинаковый способ определения степени целого уравнения, имеющего две переменные, и целого уравнения, имеющего одну переменную. Также уточняется, что уравнение, содержащее две переменные, у которого в левой части – многочлен, а в правой – 0, имеет степень, равной степени данного многочлена. Способом определения степени уравнения остается замена его равносильным уравнением таким образом, чтобы в левой части уравнения остался многочлен стандартного вида, а в левой – нуль. Приведен пример такой замены: отмечается, что уравнения (х2-у)2=х4-1 и -2х2у+у2+1=0 равносильны. После приведения уравнения к виду, когда в левой части остается многочлен стандартного вида, можно установить, что данное уравнение - третьей степени.
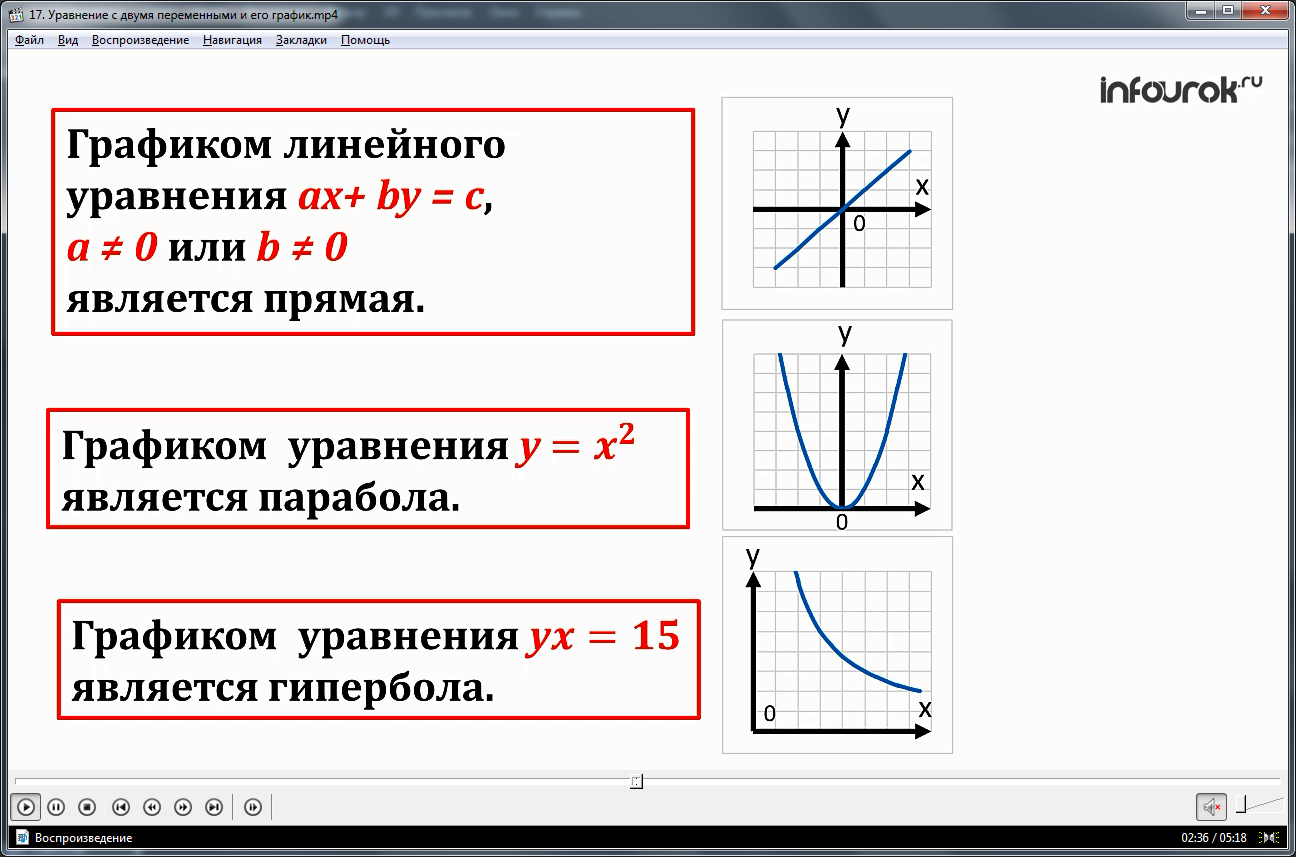
Далее рассматриваются особенности графика уравнения, имеющего две переменные. В представленном определении графиком некоторого уравнения, имеющего две переменные, является множество точек на координатной плоскости, подставив координаты которых, можно получить верное равенство. Ученикам напоминается вид графиков, уже изученных ранее и представляющих собой график уравнения с двумя переменными. Это прямая, представляющая собой график линейного уравнения ax+by=c, где a≠0 и b≠0, а также парабола – график уравнения у=х2, гипербола – график ух=15.
Ученикам демонстрируется построение графика функции x2+y2=r2, где r – произвольное положительное число. Окружность, являющаяся графиком данного уравнения, представлена на экране. Доказывается, что любая точка окружности будет удовлетворять данному уравнению. Для этого отмечаем произвольную точку В(х;у). Длина опущенного на ось абсцисс перпендикуляра равна модулю ординаты данной точки, а отрезок, проведенный из данной точки в начало координат – радиусу. Длина отрезка от начала координат до точки пересечения перпендикуляра с осью абсцисс равна модулю абсциссы. Из полученного прямоугольного треугольника АОВ имеем равенство: АО2+АВ2=ВО2, то есть |x|2+|y|2=r2. Это равенство также справедливо без знака модуля.
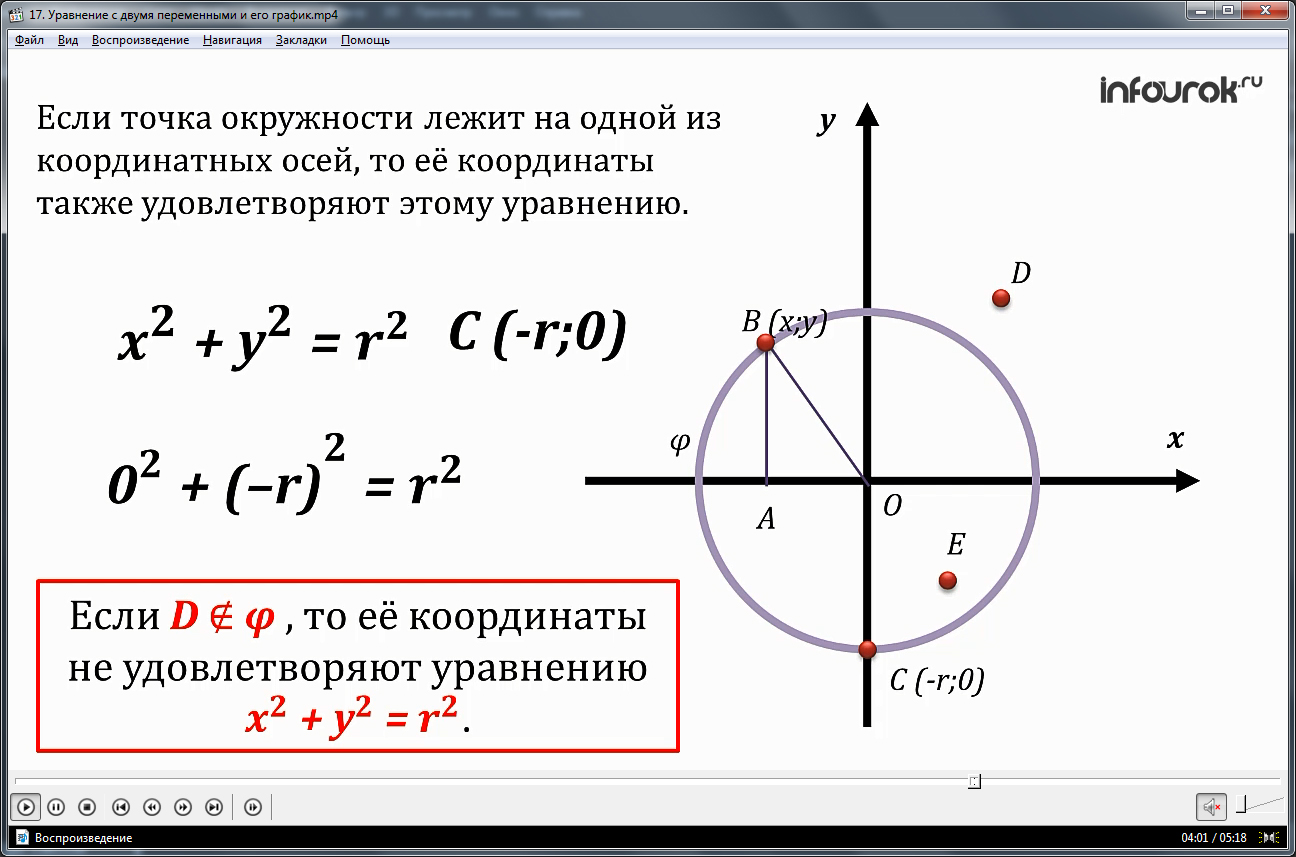
Чтобы убедиться, что уравнение верно в любом положении В(х;у) на окружности, предлагается рассмотреть точку В, которая лежит в точке пересечения окружности с осью абсцисс. Отмечается, что в этом случае одна координата точкиу равняется радиусу, а вторая – нуль. Уравнение x2+y2=r2 превращается в 02+r2=r2, поэтому равенство также справедливо. При этом для всех точек, которые не лежат в области определения, их координаты не удовлетворяют уравнению окружности x2+y2=r2. Примеры таких точек отмечены на координатной плоскости. Общий вывод из рассмотренного построения следует, что уравнение окружности в записи х2+у2=r2 верно для случаев, когда точки А(х;у) принадлежат области определения φ, О(0;0) – центр окружности, а r - радиус.
Далее рассматривается, как уравнение окружности зависит от положения ее центра. Отмечается, что при переносе центра на |а| единиц вправо или влево параллельно х, а также на |b| единиц вверх или вниз, параллельно у, получается окружность того же радиуса, только с центром в точке с новыми координатами О(a;b). Уравнением такой окружности будет (x-a)2+(y-b)2=r2.
Видеоурок «Уравнение с двумя переменными и его график» может быть использован как наглядное пособие на уроке алгебры по данной теме или заменить объяснение учителя по теме. Также данный материал может быть полезен при дистанционном обучении, поможет освоить тему ученикам самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 12700 |
| Номер материала | 663 |