
Урок «Решение неравенств методом интервалов»

Краткое описание документа:
Видеоурок «Решение неравенств методом интервалов» раскрывает содержание и смысл метода интервалов в решении неравенств. Видеоматериал содержит достаточно информации и описания примеров для освоения данного метода решения. Задача видеоурока – облегчить освоение материала, формировать умение решать неравенства.
Приемы, используемые в видеоуроке, направлены на увеличение эффективности подачи материала. Для углубления понимания метода решения используются анимационные эффекты, выделение цветом, выделение формул и понятий в рамке. При помощи видео легче воспроизвести построения и отметить промежутки, которые являются решениями данного неравенства.
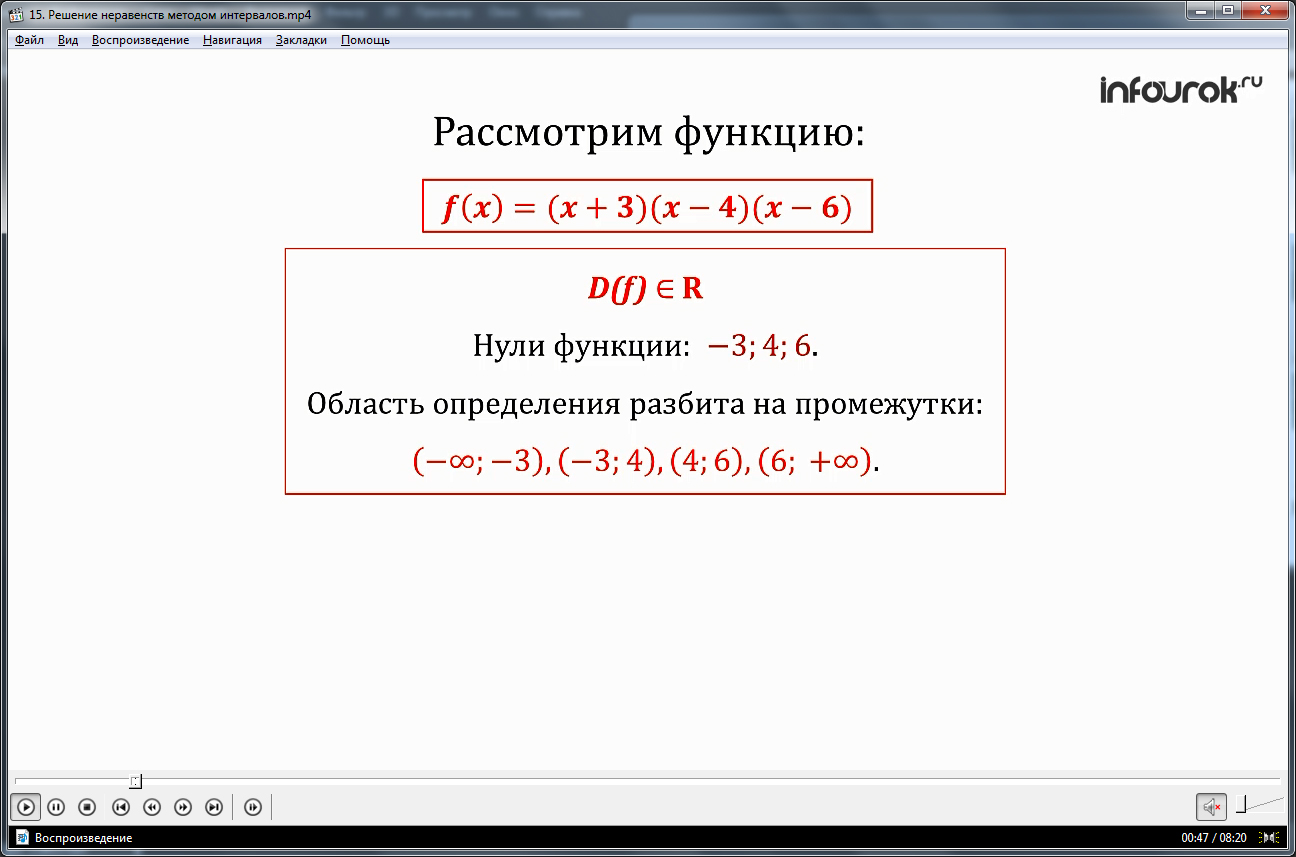
Видеоурок начинается с представления темы. Для освоения метода интервалов для решения неравенств предлагается прежде всего рассмотреть поведение функции, состоящей из множителей – линейных одночленов первой степени. Описание метода производится на примере функции f(x)=(x+3)(x-4)(x-6). В результате исследования функции отмечено, что областью определения функции будет все множество действительных чисел D(f) є R. Нулями данной функции будут -3, 4, 6 – числа, в которых функция обнуляется. Поэтому область определения данной функции разбивается на промежутки (-∞;-3), (-3;4), (4;6), (6;+∞), в каждом из которых функция обладает определенными свойствами, характеризующими значения функции. Чтобы определить знак функции на каждом из промежутков, Оценивается значение каждого множителя. Для этого в таблицу заносится промежуток и множители, оценка знака которых выполняется. Например, так как на промежутке (-∞;-3) каждый из множителей (x+3), (x-4) и (x-6) приобретают отрицательное значение, то их произведение также является отрицательным. Таким образом оценивается каждый промежуток функции. В результате анализа определяется знак функции: для (-∞;-3) f(x)<0, для (-3;4) f(x)>0, для (4;6) f(x)<0, для (6;+∞) f(x)>0. На рисунке, сопровождающем решение, отмечены интервалы, которые характеризуют знак функции и помогают оценить знак функции и проверить справедливость неравенства на том или ином промежутке. Таким образом метод интервалов помогает найти решения неравенства.

Описание решения на примере функции f(x)=(x+3)(x-4)(x-6) подводит к пониманию общей схемы применения метода интервалов. На экране представлена в общем виде функция f(x)=(x-x1)(x-x2)…(x-xn), в которой х – переменная, х1, х2,…хn – различные числа, не равные друг другу. Основное свойство данной функции – знак в каждом выделенном промежутке сохраняется, а при переходе из одного промежутка в другой знак функции меняется.
Далее представляются неравенства, которые можно решить методом интервалом. На экране выделен в рамку общий вид таких неравенств: (x-x1)(x-x2)…(x-xn)>0 и (x-x1)(x-x2)…(x-xn)<0. При этом х1, х2,…хn – различные числа, не равные друг другу.
Сформировать умения решать неравенства данного вида видеоурок помогает при помощи описания решения в наиболее характерных случаях. В первом примере предлагается решить неравенство (x+7)(x+2)(x-3)<0. Согласно используемому методу интервалов поведение функции оценивается в точках х1=-7, х2=-2, х3=3. Отмечены промежутки, на которые разбивается область определения: (-∞;-7), (-7;-2), (-2;3), (3;+∞). На рисунке, сопровождающем решение неравенства, отмечен знак функции, приобретаемый в каждом из промежутков. В результате анализа, что необходимое условие отрицательных значений функций соблюдается на промежутках (-∞;-7) и (-2;3). Объединение данных промежутков и будет решением задачи. Для лучшего запоминания метода решения, его название выводится на экран и выделяется цветом и восклицательным знаком.

Следующим рассматривается решение неравенства х(1-x)(x+5)<0. Основная особенность данного неравенства – наличие в формуле отрицательного х. Чтобы решить такое неравенство методом интервалов, его приводят к виду (x-x1)(x-x2)…(x-xn)<0. Для этого множитель -1 выносится за скобки. В результате чего неравенство преобразуется в вид: -х(x-1)(x+5)<0 или х(x-1)(x+5)>0. Данное преобразование дает возможность оценить знаки функции в образуемых нулями промежутках. На сопровождающей решение иллюстрации схематично отмечаются найденные промежутки и знак функции на них. Очевидно, знак значений функции будет отрицательным на промежутках (-5;0) и (1; +∞). Объединение данных промежутков является решением неравенства.
Пример 3, рассматривающий описание решения неравенства (5x+1)(2-x)>=0, обращает внимание учеников на использование в неравенстве знака >= и закрепляет умение преобразовывать неравенство к виду, походящему для применения метода интервалов. Для обращения левой части неравенства в выражение вида (x-x1)(x-x2)…(x-xn) за скобки выносится общий множитель 5 из первого линейного выражения и множитель -1 из вторых скобок. В результате преобразований неравенство приводится к виду (х+1/5)(х-2)<=0. Оценивается знак функции f(x)=(х+1/5)(х-2) на промежутках (-∞;-1/5], [-1/5;2], [2;+ ∞). Обращается внимание учеников на то, что в данном неравенстве промежутки включают нули функции, так как неравенство нестрогое. В результате анализа видно, что неравенство верно на промежутке [-1/5;2].
Также отмечается, что решить методом интервалов можно неравенства, левая часть которых представляет собой дробь, числитель и знаменатель которой – многочлен первой степени. Чтобы применить метод интервалов, выражение (8-х)/(х+1)<0 в левой части преобразуется к виду (x-x1)(x-x2)…(x-xn). Для этого обе части неравенства умножаются на знаменатель дроби. В результате анализа нулей функции оценивается ее знак на различных промежутках. Очевидно, условию неравенства будут удовлетворять интервалы (-∞;-1) и (8;+ ∞). Так как неравенство строгое, нули функции не входят в решение.
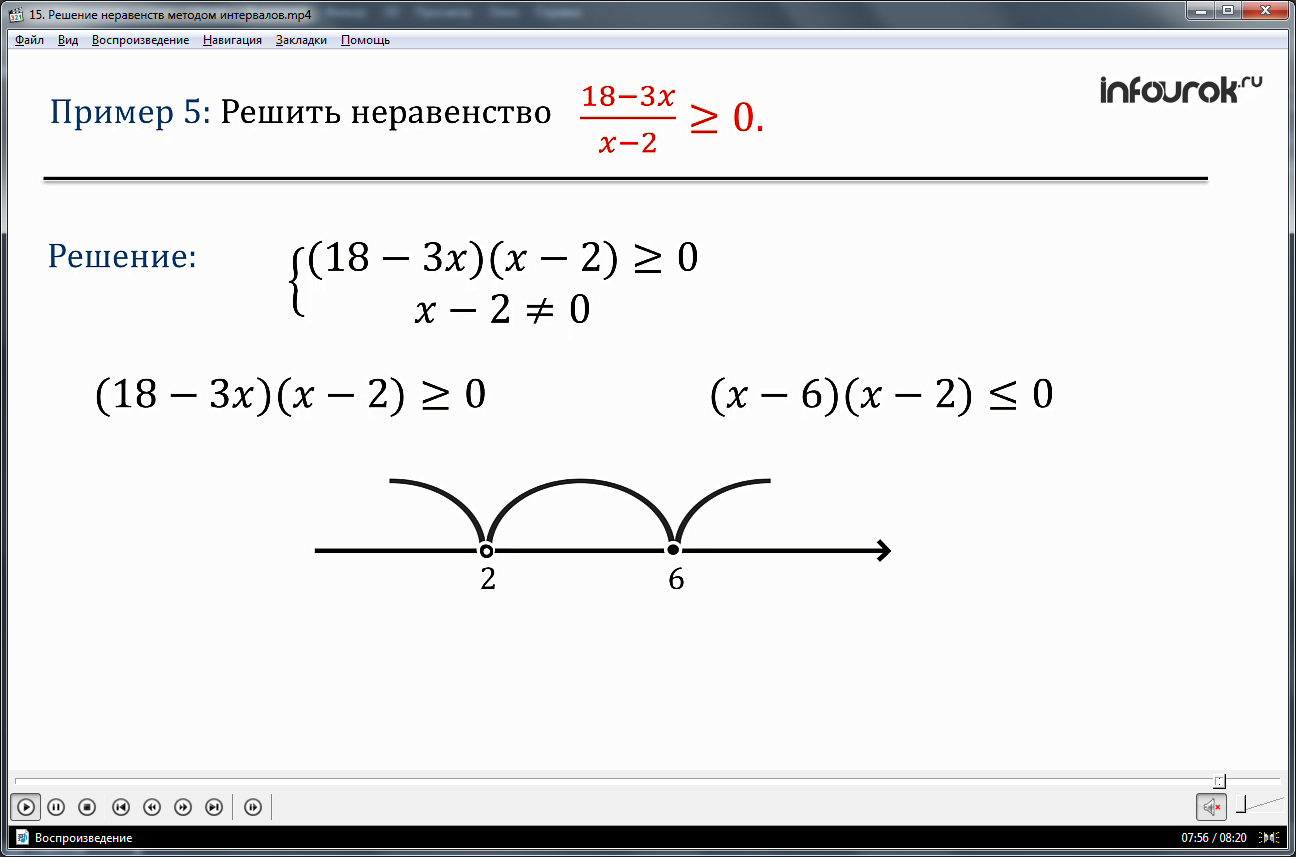
Последний пример, рассмотренный в видеоуроке, описывает решение неравенства (18-3х)/(х-2)>=0. Обращается внимание, что решение уравнения не может обращать в нуль его знаменатель, поэтому при анализе интервалов, обязательно учитывается, что х-2≠0. При умножении обеих частей неравенства на знаменатель дробной части (х-2), образуется неравенство в виде, который дает возможность применить метод интервалов: (18-3х)(х-2)>=0. После вынесения множителя 3 за скобки, получаем интервалы для анализа: (-∞;2), (2;6), (6;+ ∞). Очевидно, условиям неравенства соответствует промежуток (2;6).
Видеоурок «Решение неравенств методом интервалов» может помочь учителю объяснить суть и применение метода интервалов для решения неравенств на уроке в школе. Также подробное описание решения поможет ученику самостоятельно рассмотреть тему. Будет полезен материал и в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11887 |
| Номер материала | 662 |