
Урок «Системы неравенств с двумя переменными»

Краткое описание документа:
Видеоурок «Системы неравенств с двумя переменными» содержит наглядный учебный материал по данной теме. В урок включено рассмотрение понятия о решении системы неравенств с двумя переменными, примеров решения подобных систем графическим способом. Задача данного видеоурока – формировать умение учеников решать системы неравенств с двумя переменными графическим способом, облегчить понимание процесса поиска решений таких систем и запоминания метода решения.
Каждое описание решения сопровождается рисунками, которые отображают решение задачи на координатной плоскости. На таких рисунках наглядно показаны особенности построения графиков и расположения точек, соответствующих решению. Все важные детали и понятия выделены при помощи цвета. Таким образом, видеоурок является удобным инструментом для решения задач учителя на уроке, освобождает учителя от подачи стандартного блока материала для проведения индивидуальной работы с учениками.
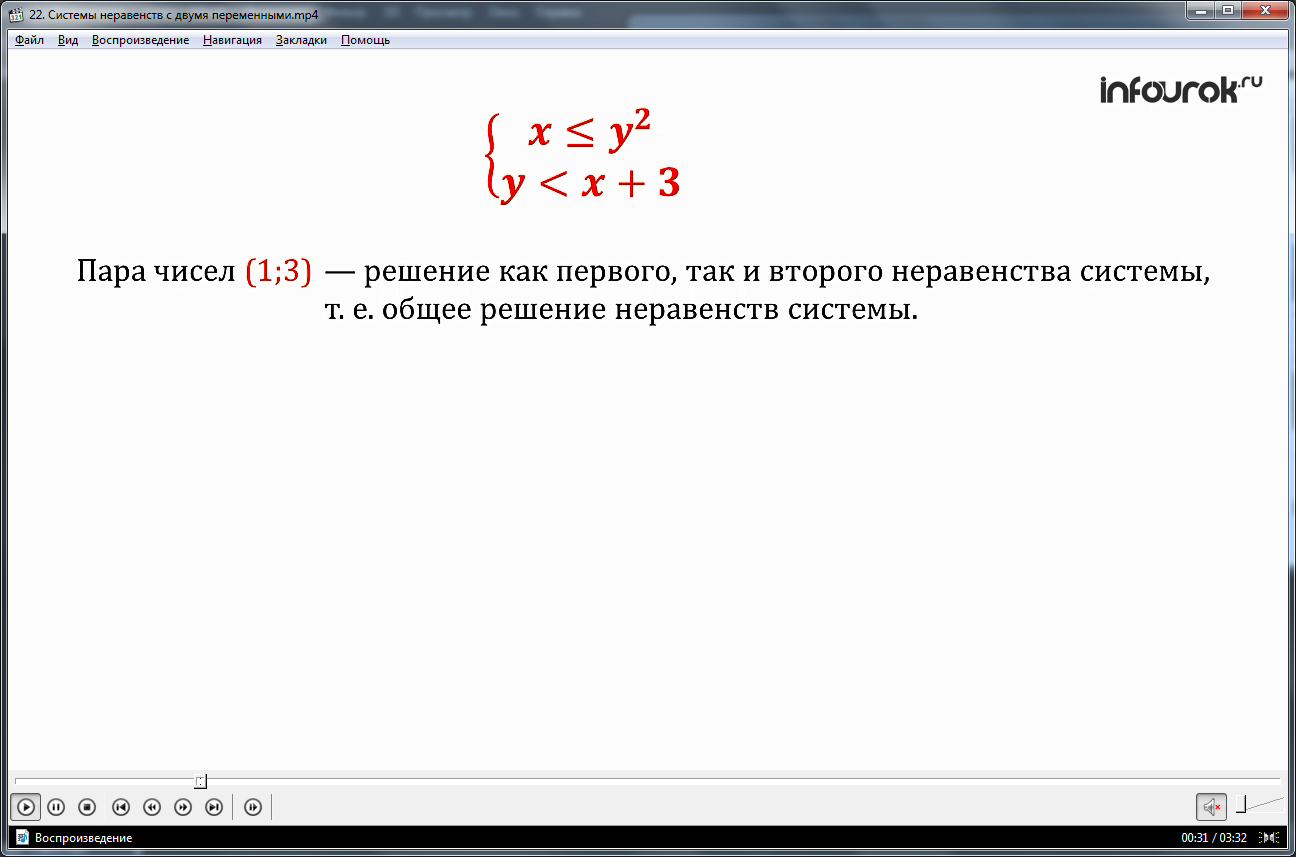
Видеоурок начинается с представления темы и рассмотрения примера поиска решений системы, состоящей из неравенств x<=y2 и у<х+3. Примером точки, координаты которой удовлетворяют условиям обеих неравенств, является (1;3). Отмечается, что, так как данная пара значений является решением обоих неравенств, то она является одним из множества решений. А все множество решений будет охватывать пересечение множеств, которые являются решениями каждого из неравенств. Данный вывод выделен в рамку для запоминания и указания на его важность. Далее указывается, что множество решений на координатной плоскости представляет собой множество точек, которые являются общими для множеств, представляющих решения каждого из неравенств.

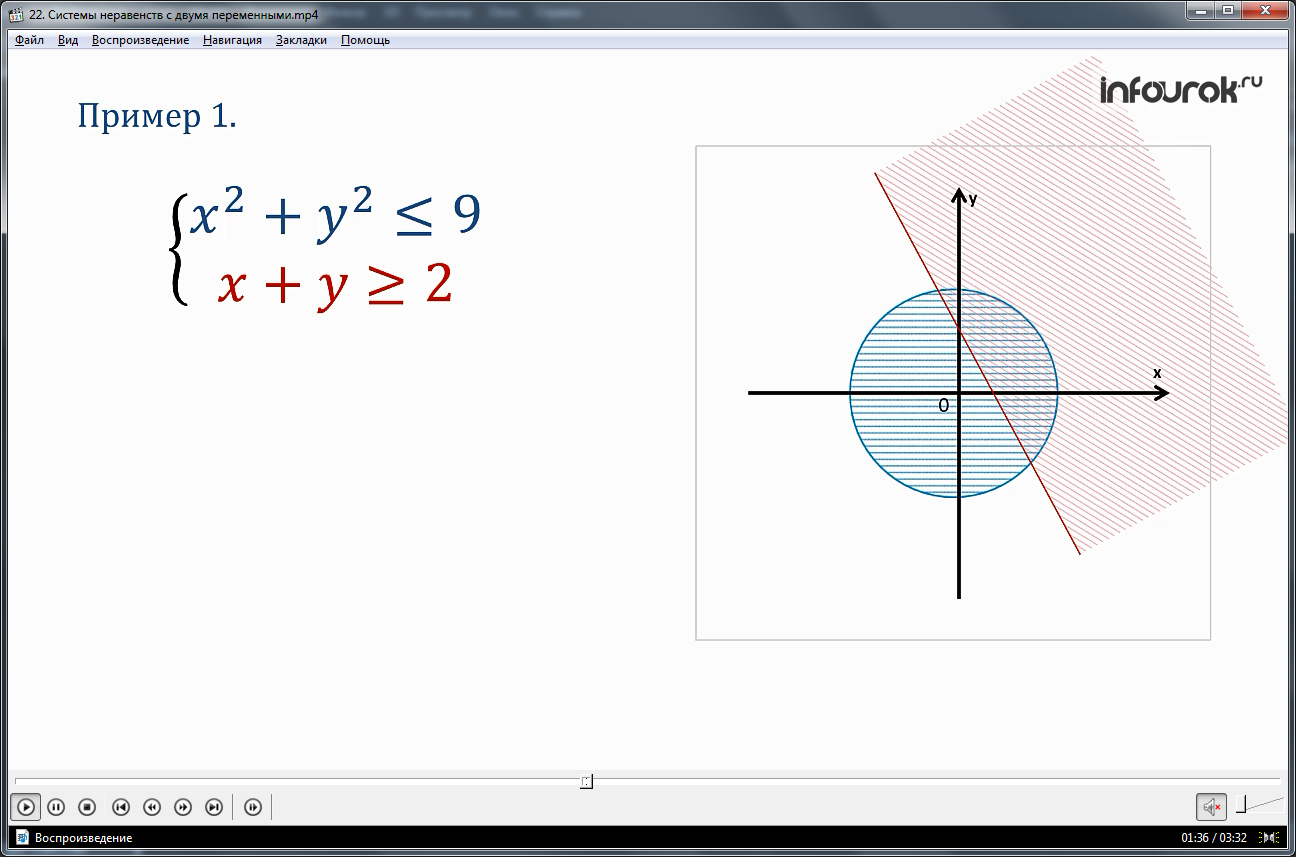
Понимание сделанных выводов о решении системы неравенств закрепляется рассмотрением примеров. Первым рассматривается решение системы неравенств х2+у2<=9 и x+y>=2. Очевидно, что решения первого неравенства на координатной плоскости включают окружность х2+у2=9 и область внутри нее. Эта область на рисунке заполняется горизонтальной штриховкой. Множество решений неравенства x+y>=2 включает прямую x+y=2 и полуплоскость, расположенную выше. Данная область также обозначается на плоскости штрихами другого направления. Теперь можно определить пересечение двух множеств решений на рисунке. Оно заключено в сегменте круга х2+у2<=9, который покрыт штриховкой полуплоскости x+y>=2.
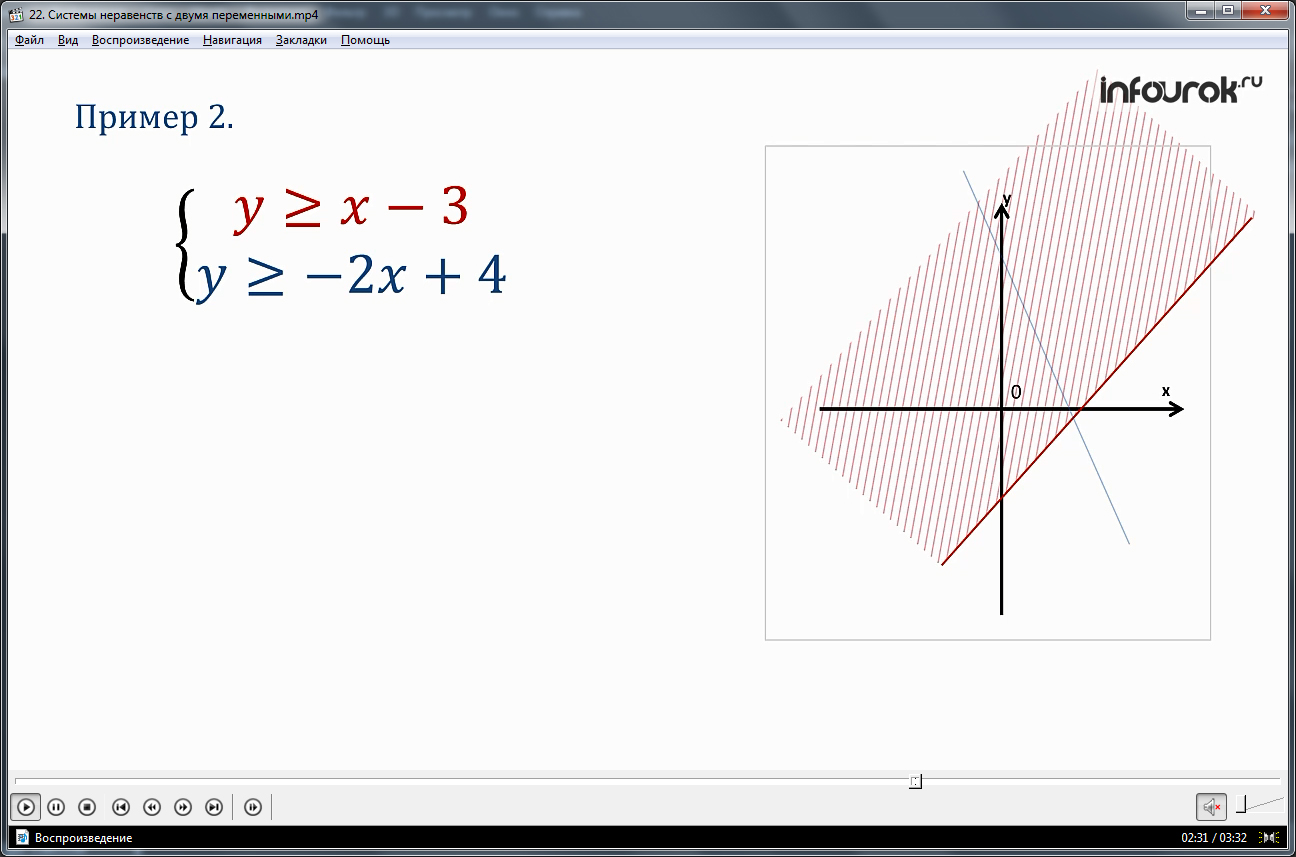
Далее разбирается решение системы линейных неравенств y>=x-3 и y>=-2x+4. На рисунке рядом с условием задания строится координатная плоскость. На ней строится прямая, соответствующая решениям уравнения y=x-3. Областью решения неравенства y>=x-3 будет область, расположенная над данной прямой. Она заштриховывается. Множество решений второго неравенства располагается над прямой y=-2x+4. Данная прямая также строится на той же координатной плоскости и область решений штрихуется. Пересечением двух множеств является угол, построенный двумя прямыми, вместе с его внутренней областью. Область решений системы неравенств заполнена двойной штриховкой.
При рассмотрении третьего примера описан случай, когда графиками уравнений, соответствующих неравенствам системы, являются параллельные прямые. Решить необходимо систему неравенств y<=3x+1 и y>=3x-2. На координатной плоскости строится прямая, соответствующая уравнению y=3x+1. Область значений, соответствующих решениям неравенства y<=3x+1, лежит ниже данной прямой. Множество решений второго неравенства лежит выше прямой y=3x-2. При построении отмечается, что данные прямые параллельны. Область, являющаяся пересечением двух множеств решений, представляет собой полосу между данными прямыми.
Видеоурок «Системы неравенств с двумя переменными» может применяться в качестве наглядного пособия на уроке в школе или заменить объяснение учителя при самостоятельном изучении материала. Подробное понятное объяснение решения систем неравенств на координатной плоскости может помочь подать материал при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11828 |
| Номер материала | 666 |