
Урок «Решение неравенств второй степени с одной переменной»

Краткое описание документа:
Видеоурок «Решение неравенств второй степени с одной переменной» представляет информацию о способах решения неравенств второй степени с одной переменной. Тема важная для решения многих практических задач, которые могут возникнуть в ходе изучения других разделов математики, физики. Видеоурок содержит материал, составляющий теоретическую основу решения, а также множество примеров, которые демонстрируют применение данных способов. Задача видеоурока – помочь пониманию, запоминанию учениками способов решения подобных неравенств.
В ходе видеоурока используются анимационные эффекты, иллюстрации, наглядно демонстрирующие особенности изучаемых понятий. Детальное описание решения неравенств, в котором важные понятия и детали выделены цветом, анимированы, помогает быстрее сформировать умения е их решать.
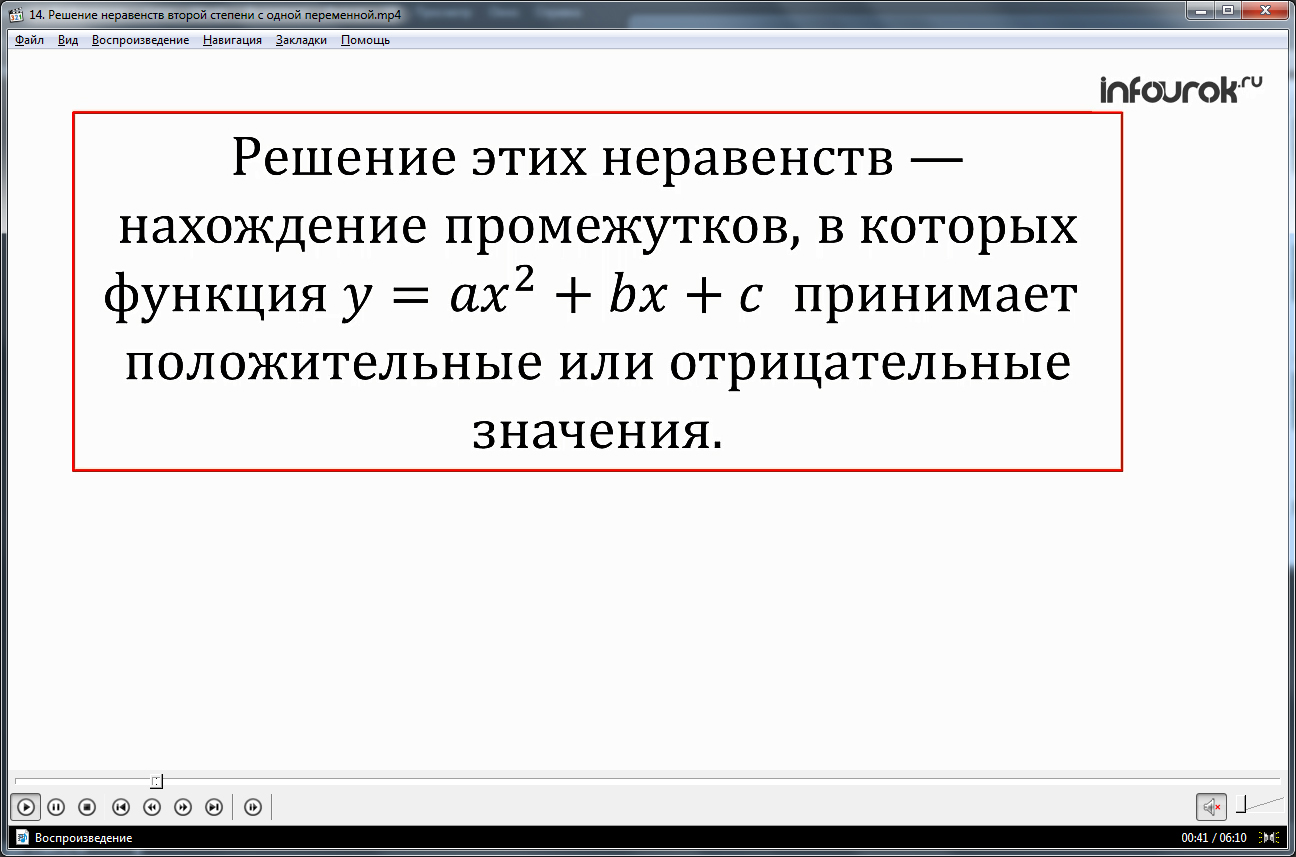
Видеоурок начинается с представления темы, после чего дается определение неравенства второй степени с одной переменной. На экране отображаются неравенства, которые входят число изучаемых выражений: ax2+bx+c>0, ax2+bx+c<0. Также отмечается, что в данных выражениях х – переменная, a, b, c – числа, среди которых а≠0. Далее выделяется особенность решения неравенств второй степени с одной переменной. Оно сводится к нахождению промежутков, в которых у=ax2+bx+c принимает отрицательные или положительные значения. Проанализировать данную особенность решения предлагается на графике функции у=ax2+bx+c. Чтобы отметить особенности решения неравенства при помощи графика функции, нужно выполнить ее исследования, то есть отметить, куда смотрят ветви параболы, пересекает ли и каким образом ось координат х.
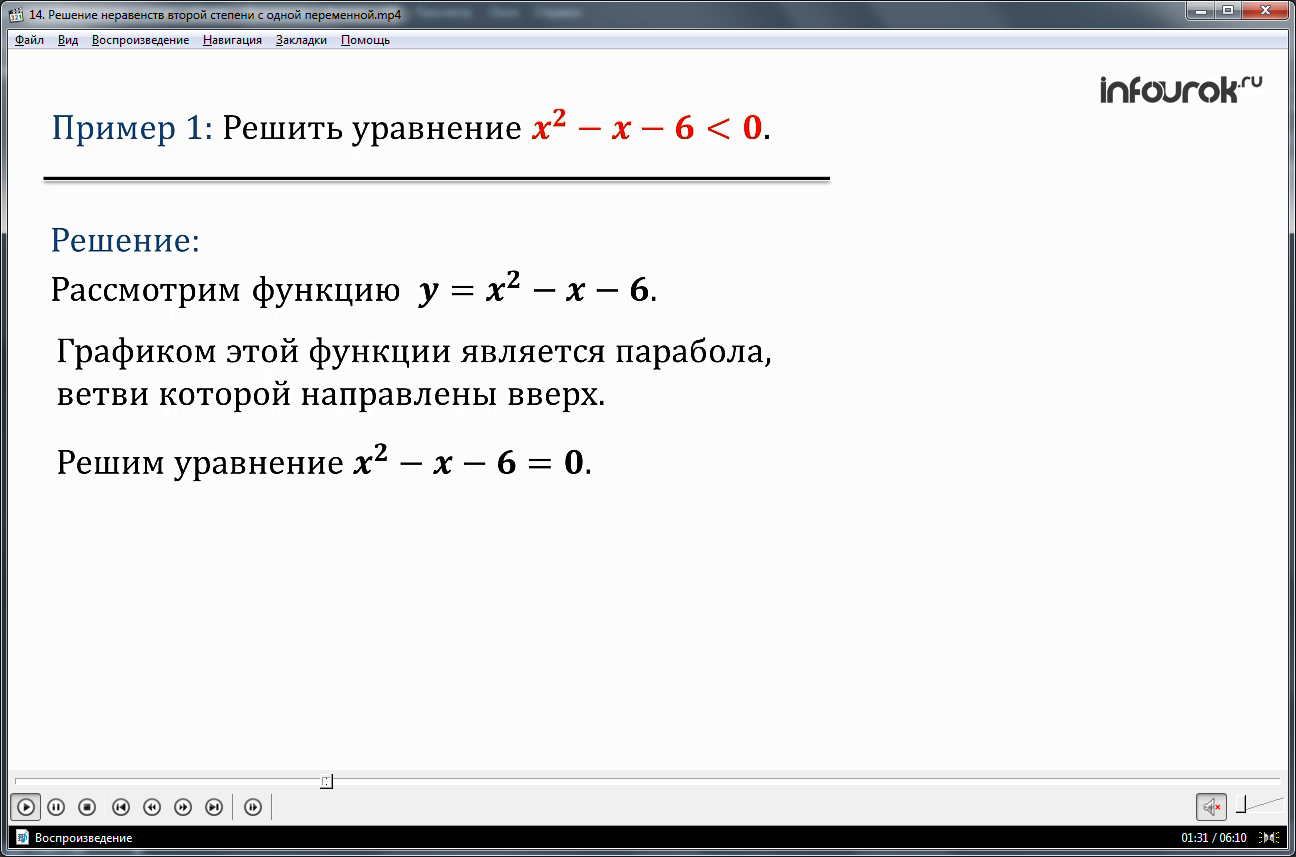
Далее рассматривается решение задачи, в которой необходимо найти решение неравенства х2-х-6<0. Чтобы определить область решений, необходимо сначала исследовать функцию у=x2-x-6. Согласно изученному ранее материалу, известно, что ветви данной параболы направлены вверх, так как старший коэффициент многочлена положительный. Чтобы определить нули функции, приравниваем ее к нулю: x2-2x-6=0. Решив данное уравнение, получаем две точки пересечения параболы осью х: х1=-2, х2=3. При помощи иллюстрации ученикам демонстрируется построение параболы, являющейся графиком данной функции с точками пересечения оси х в х1=-2, х2=3. Отмечается, что значения, меньше нуля, данная функция принимает на промежутке между точками пересечения, то есть х ϵ (-2;3).
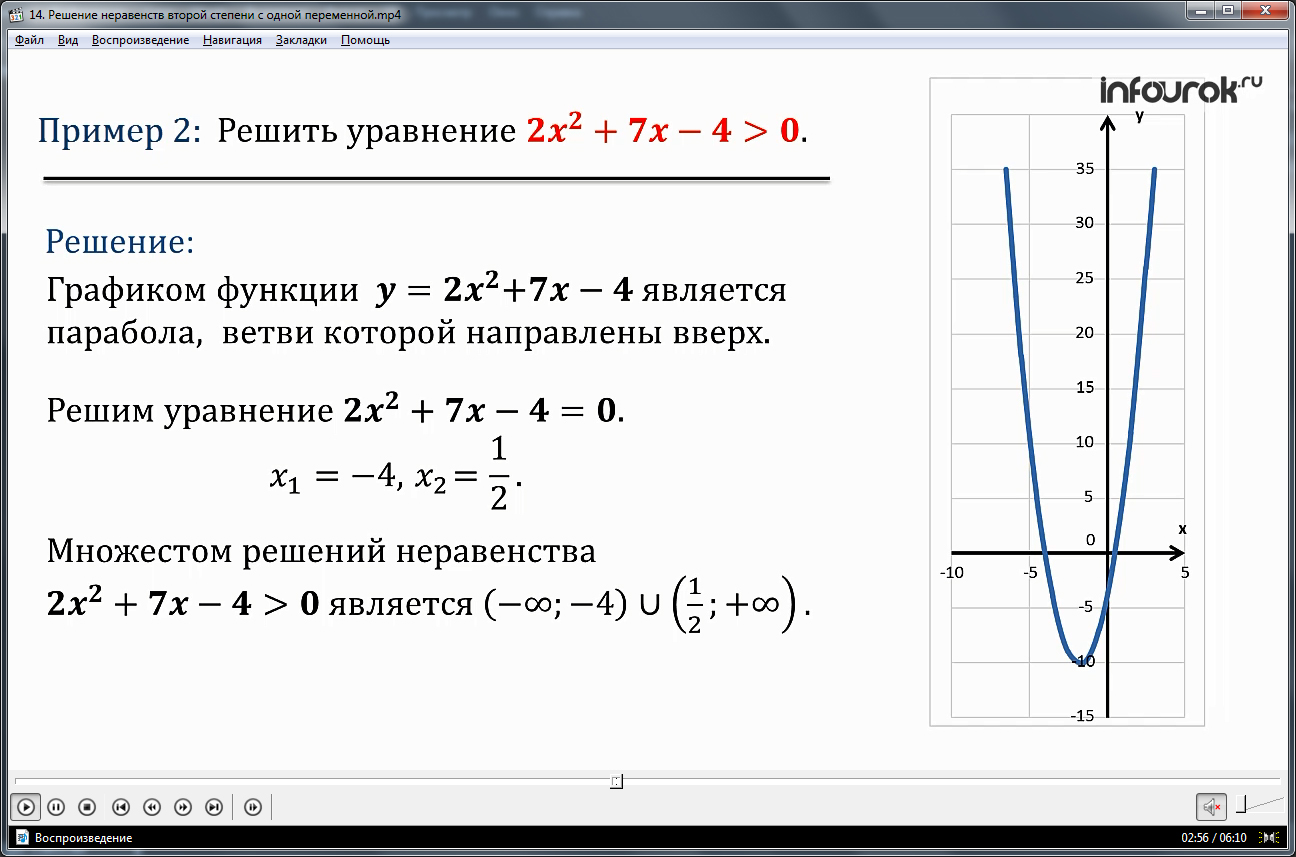
Во втором примере необходимо найти решение неравенства 2х2+7х-4>0. Описывается решение данного неравенства, начиная с указания, что графиком соответствующей функции у=2х2+7х-4 будет парабола, ветви которой направлены вверх. Чтобы определить ее точки пересечения с осью абсцисс, находится решение уравнения 2х2+7х-4=0. После проведенных вычислений определяется, что х1=-4, х2=1/2. На графике, построенном рядом с описанием решения, видно, что положительные значения функция принимает на промежутках (-∞; -4) и (1/2; +∞). Соответственно, решением данного неравенства будет объединение указанных промежутков.
Следующий пример 3 описывает решение неравенства, в котором старший коэффициент многочлена отрицательный: -1/2х2+4х-8<0. Для решения данного неравенства требуется построить график функции у=-1/2х2+4х-8. Так как старший коэффициент многочлена отрицательный, ветви параболы смотрят вниз. После вычисления корень уравнения -1/2х2+4х-8=0 оказывается равным х=4.В точке х=4 парабола пересекает ось абсцисс, она является и вершиной параболы. Соответственно, все значения данной функции будут лежать ниже нуля и удовлетворять требованиям условия задания. Решением неравенства будет объединение промежутков (-∞; 4) и (4; +∞). В ответе указано. Что решением неравенство будет любое число, не равное 4.
В примере 4 предлагается найти решение неравенства х2-10х+31>0. Вначале отмечается, что графиком функции у= х2-10х+31 будет парабола, ветви которой направлены вверх. После поиска корней уравнения х2-10х+31=0 выясняется, что точек пересечения функции с осью абсцисс нет. Так как на всей координатной оси функция принимает положительные значения, решением будет любое значение х.
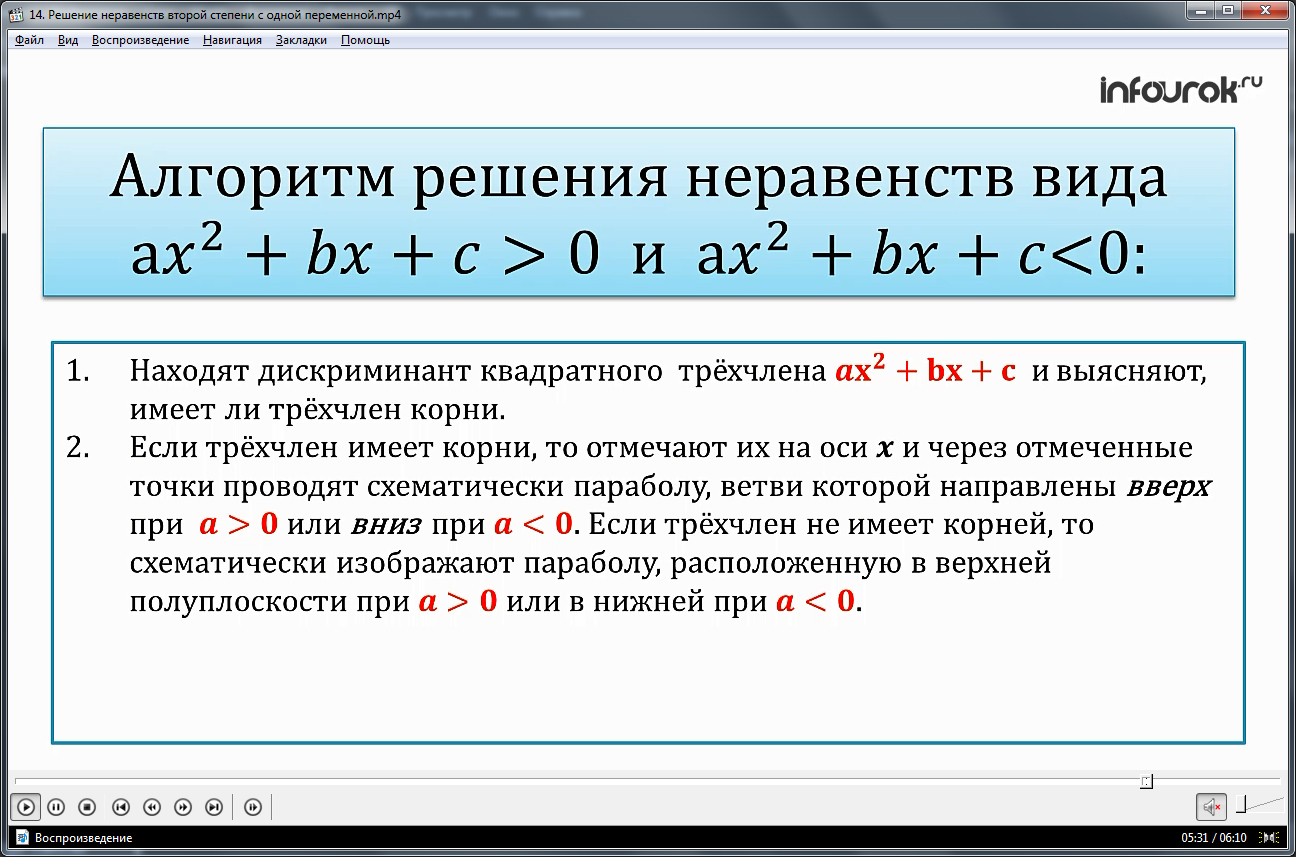
После описания решения подобных заданий на примерах, проводится обобщение способа решения подобных задач. Алгоритм решения выделен в отдельную таблицу, которая предлагается для запоминания. В таблице поэтапно расписано решение. Первый этап решения состоит в вычислении дискриминанта квадратного трехчлена, соответствующего неравенству ax2+bx+c>0 или ax2+bx+c<0. Определяется наличие и количество корней уравнения ax2+bx+c=0. На следующем этапе в случае наличия корней данного уравнения, полученные значения отмечаются на оси х как точки пересечения параболы с осью абсцисс. Строится парабола. Ветви параболы направляют вниз, если в квадратном трехчлене а<0, и ветви параболы направляют вверх, если а >0. Для решения данного задания достаточно схематического построения параболы с учетом выявленных особенностей. На последнем этапе решения определяются промежутки на оси х, которые в параболе для решения ax2+bx+c>0 расположены выше оси абсцисс. При решении ax2+bx+c<0 решением неравенства являются промежутки, которые соответствуют отрицательным значениям функции у=ax2+bx+c.
Видеоурок «Решение неравенств второй степени с одной переменной» может послужить заменой объяснению учителем стандартного блока материала для формирования навыков решения неравенств второй степени. Подробное понятное объяснение будет полезным для тех, кто желает самостоятельно освоить тему. Также данный материал поможет преподавателю, проводящему дистанционное обучение.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7424 |
| Номер материала | 661 |