
Урок "Построение графиков прямой и обратной числовой функции"

Краткое описание документа:
Навык построения графиков функций считается одним из самых важных в процессе обучения математике. Чтобы обучающиеся легко этот навык получили и выработали, важно тщательно подбирать средства обучения. Одним из наиболее эффективных таких средств считается видеоурок.
Данный видеоурок разработан автором с целью облегчить работу учителя. То время, которое учитель тратит на подготовку к уроку, разбору материала по теме, он может посвятить другим более важным делам.
Трансляция урока занимает 6:39 минут. Примерно столько же времени затрачивает учитель, когда объясняет материал сам, без помощи таких средств обучения, как видеоуроки. Но довольно часто обучающиеся стараются завлечь учителя какими-нибудь отвлеченными разговорами. Этот номер не пройдет ,если учитель станет использовать видеоурок. Здесь обучающимся никуда не деться, они будут внимательно слушать и записывать. Поэтому результат должен получиться более устойчивым.
Материал данного урока четко структурирован. Изложение не лишено логики. В самом начале предлагается рассмотреть некоторую обратимую функцию на некоторой области определения и ее обратную функцию.
Далее автор вспоминает свойства прямой и обратной функции, говоря, что они связаны между собой. Эти свойства появляются на экране поочередно, каждое из них подробно поясняется.
После рассмотренных свойств показано, как получаются графики прямой и обратной функций. Все это демонстрируется на рисунке. Подробно, четко и наглядно. Затем на экране появляется правило, которое рекомендуется запомнить. Это правило содержит в себе всю информацию о том, как строится график обратной функции. И затем рисунок показывает, как выглядят прямая и обратная функции на графике.
После того, как обучающиеся познакомятся с теоретическим материалом, предлагается рассмотреть ,как теория применяется на практике. Для этого автор предлагает рассмотреть два примера, где за основу взяты совершенно разные функции. В первом примере показано, как строится график функции обратной линейной функции. А во втором примере рассмотрена квадратичная функция и ее график. В обоих случаях сначала предлагается выразить из прямой функции ей обратную аналитически, а затем уже построить график обратной функции, конечно, после того, как построен график прямой функции.
На этом видеоурок заканчивается. И учитель может ограничиться только тем материалом, который предлагается здесь. Хотя было бы справедливо, рекомендовать учителю после рассмотрения материала данного видеоурока закрепить материал с помощью дополнительных упражнений, которые предстоит подобрать учителю в соответствии со способностями обучающихся.
Данный видеоурок может быть использован учителем на уроке для объяснения нового материала, а также обучающимися для самостоятельной подготовки к уроку по данной теме или в случае самообразования.
ТЕКСТОВАЯ РАСШИФРОВКА:
Построение графиков прямой и обратной числовой функции.
Вспомним определение обратной функции и ее свойства.
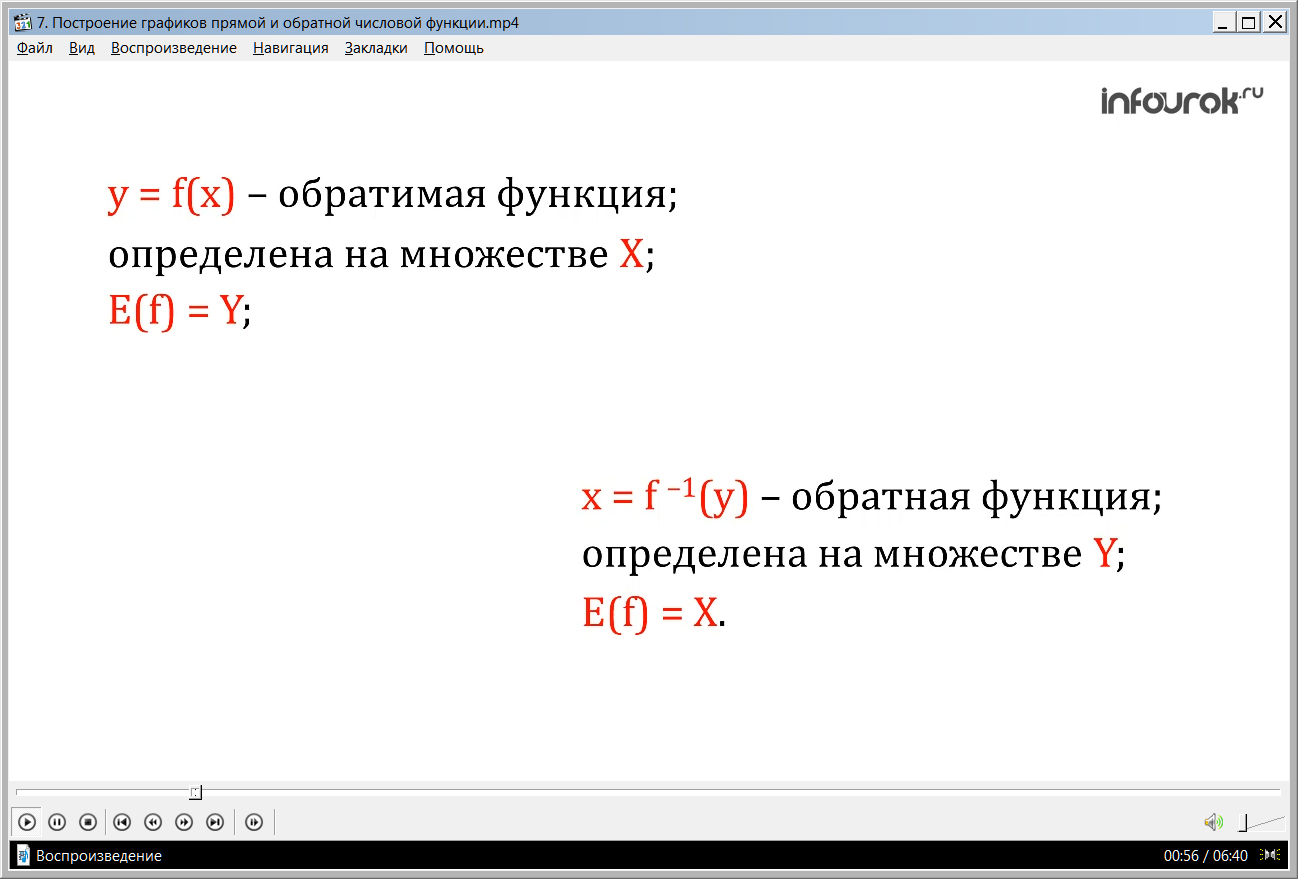
Пусть обратимая функция игрек равно эф от икс определена на множестве икс большоеи область значений есть множество игрек большое. Поставим в соответствие каждому игрек из множества игрек большое. то единственное значение икс, при котором эф от иксравно игрек. Тогда получим функцию, которая определена на множестве игрек большое, а икс большое – область значений функции.
Эту функцию обозначают икс равно эф в минус первой степени от игрек и называют обратной по отношению к функции игрек равно эф от икс .
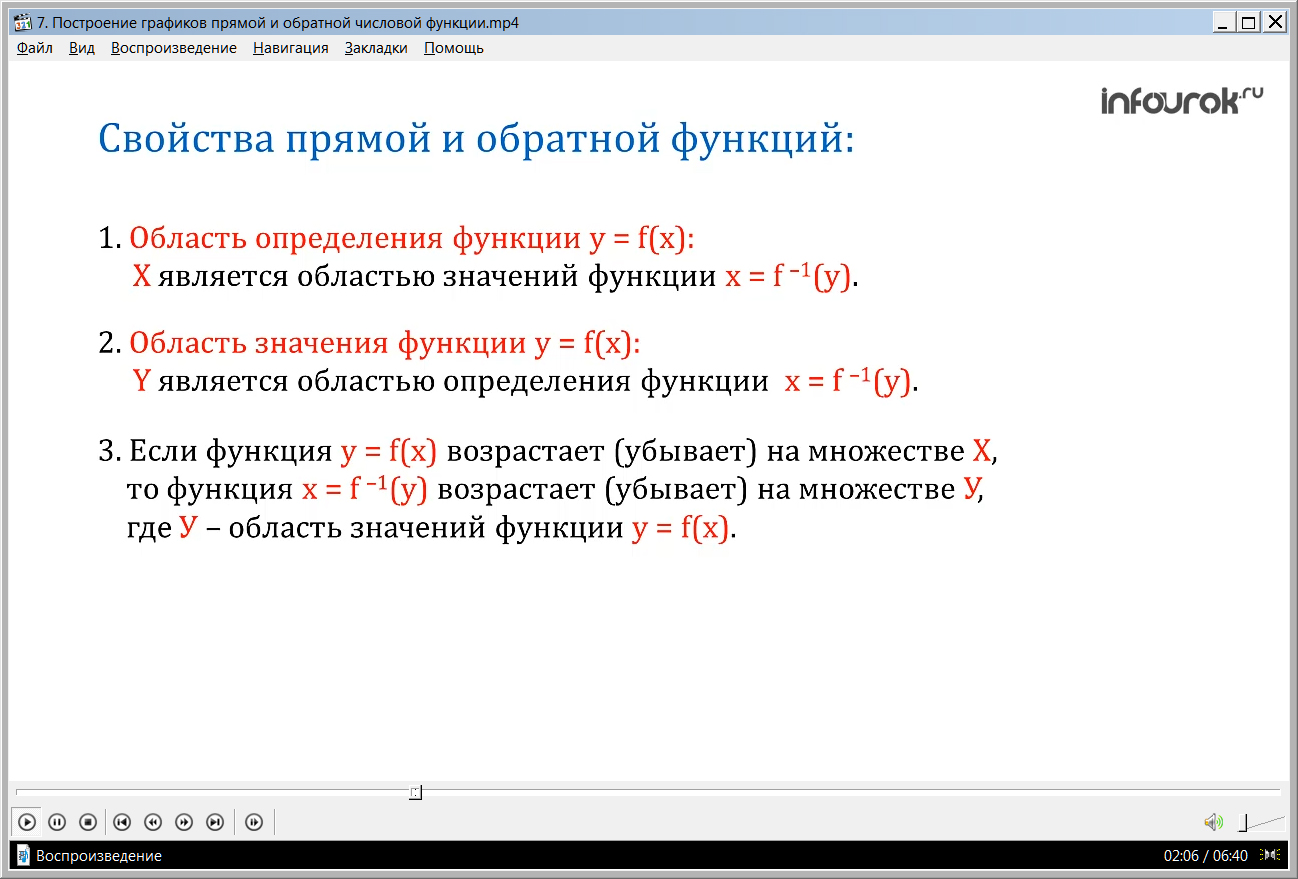
свойства прямой и обратной функций, связаны между собой.
Итак, мы видим, что переход от функции игрек равно эф от икс, где икс из икс большое к обратной функции икс равно эф в минус первой степени от игрек, где игрек из игрек большое сводится к замене множеств икс на игрек: в первом случае икс на игрек, а во втором игрек на икс, тогда зависимость между икс и игрек одна и та же в обоих случаях. Значит, и графики функций
игрек равно эф от икс и икс равно эф в минус первой степени от игрек на координатной плоскости икс о игрек представляют собой одно и то же множество точек.
Если же условиться, что, как обычно, независимую переменную (т. е. аргумент) обозначить через икс, а зависимую переменную через игрек, то пара чисел икс точка с запятой игрек удовлетворяет уравнению игрек равно эф от икс или эквивалентному ему икс равно эф в минус первой степени от игрек, а уравнению
игрек равно эф в минус первой степени от икс - пара чисел игрек точка с запятой икс. Следовательно график функции игрек равно эф в минус первой степени от икс получается из графика функции игрек равно эф от икс с помощью осевой симметрии относительно прямой игрек равно икс
( биссектрисы первого и третьего координатных углов).
Запомни: чтобы получить график функции
игрек равно эф в минус первой степени от икс, которая является обратной к функции игрек равно эф от икс надо график функции игрек равно эф от икс отобразить симметрично относительно прямой игрек равно икс.
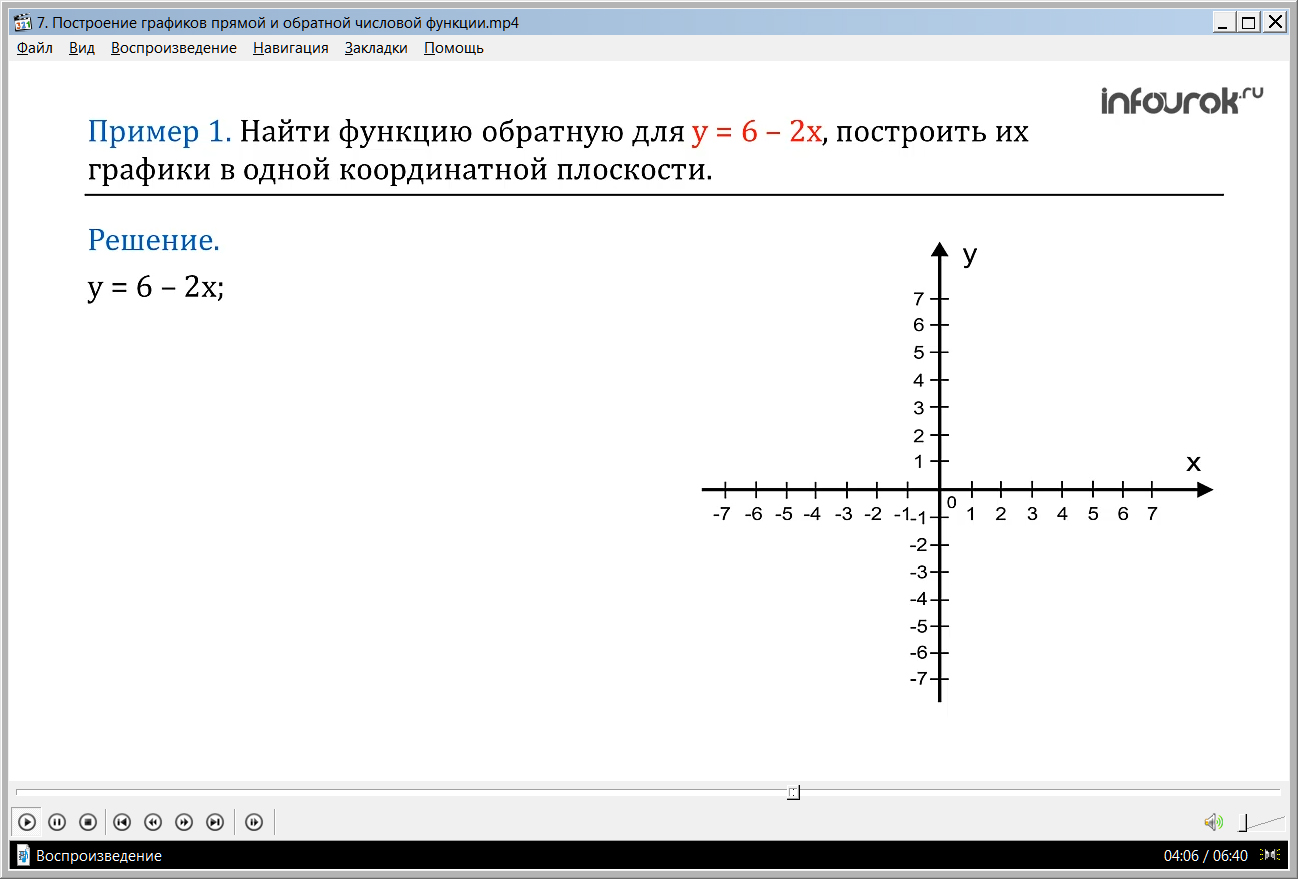
Пример первый. Найти функцию обратную для функции игрек равно шесть минус два икс,
построить их графики в одной координатной плоскости. Решение.
Функция игрек равно шесть минус два икс убывает на всей области определения. Дэ большое от икс равно эр большое Она имеет обратную ей функцию.
Обозначим игрек равно три минус ноль целых пять десятых икс – это и есть обратная функция.
Построим график функции игрек равно шесть минус два икс .Для этого берем пару различных точек, например, с координатами ноль и шесть и три и ноль. Строим их в координатной плоскости икс о игрек. Так как график обратной функции симметричен относительно прямой игрек равно икс, то достаточно построить точки , симметричные данным точкам относительно прямой игрек равно икс
Нетрудно догадаться, что эти точки будут иметь такие координаты шесть и ноль и ноль и три. (то есть икс и игрек меняются местами) Через полученные точки проводим прямую, тем самым получим график обратной функции.
Пример третий
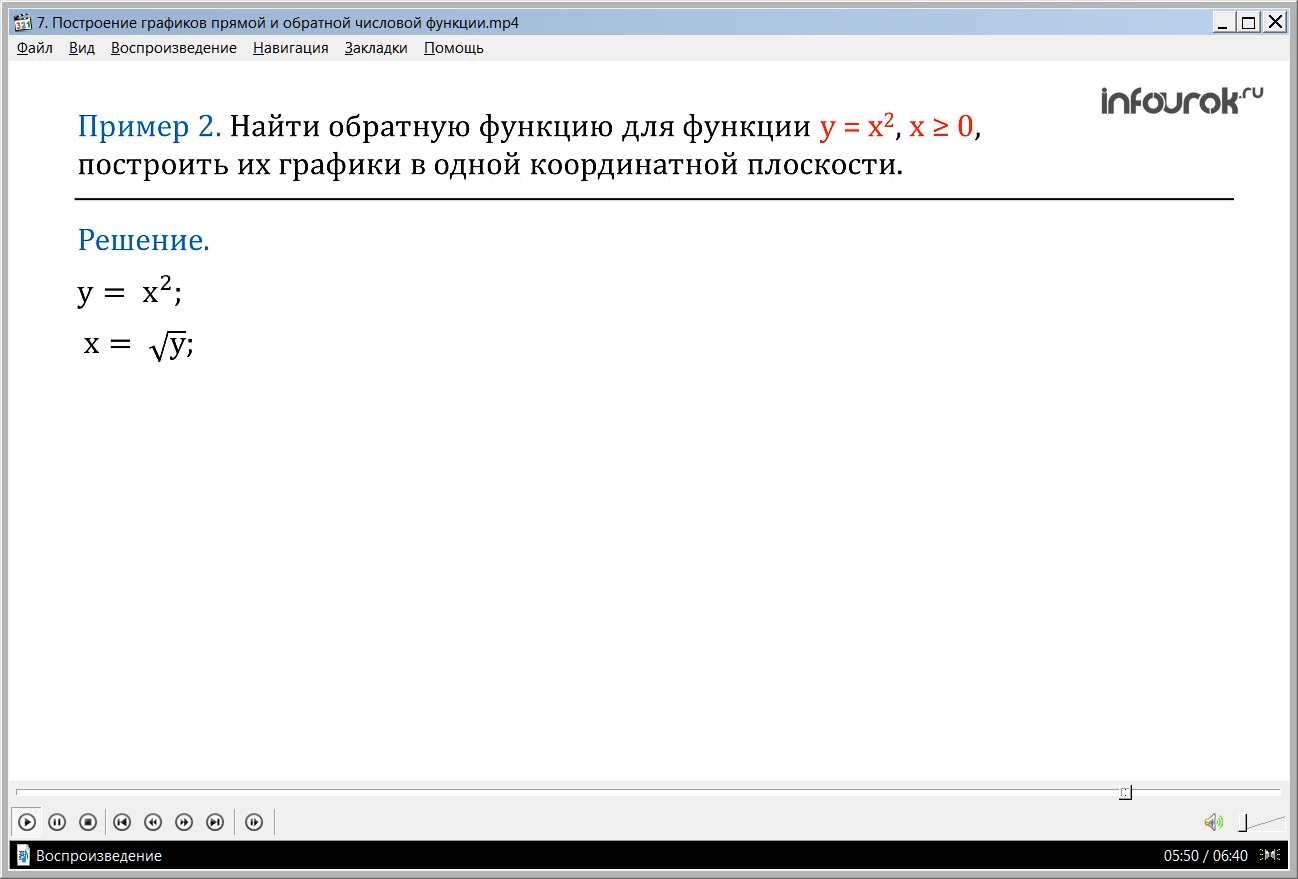
Найти обратную функцию для функции игрек равен икс квадрат, где икс больше или равен нулю, построить их графики в одной координатной плоскости.
Решение.
Сначала отметим, что прямая функция монотонно возрастает, значит, для нее существует обратная функция, которая тоже будет монотонно возрастать.
Выполняем ряд преобразований.
Извлекаем квадратный корень из обеех частей уравнения у=х2, получим ,
Переобозначих переменные
(икс заменяем на игрек)
Обратная функция найдена: игрек равен квадратный корень из икс , где
где икс больше или равно нулю
Рассмотрим график функции игрек равен икс квадрат, где икс больше или равен нулю.
График функции игрек равен икс квадрат нам известен, в данном случае является ветвь параболы на интервале от нуля до плюс бесконечности.
Далее проводим ось симметрии игрек равен икс и отображаем кривую относительно этой прямой – график обратной функции получен.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5055 |
| Номер материала | 830 |