
Урок "Построение правильных многоугольников"

Краткое описание документа:
Видеоурок «Построение правильных многоугольников» раскрывает одноименную тему. В ходе изучения курса математики при решении практических задач может возникнуть необходимость построить правильный многоугольник для графического представления или решения задачи. В этом случае нужно уметь произвести такие построения. В ходе данного видеоурока формируется умение строить правильные многоугольники при помощи циркуля и линейки. Задача видеоматериала – облегчить усвоение материала, формировать умение производить корректные построения, способствовать запоминанию материала.

Для достижения задач учителя в видеоуроке используются анимационные эффекты. Они приближают построения к построениям, выполняемым при помощи чертежных инструментов на бумаге или на доске в классе. Озвучивание процесса построения диктором позволяет создать полноценный обучающий процесс, который может при необходимости контролироваться учителем. Материал может послужить наглядным пособием, сопровождающим объяснение учителя или заменить объяснение учителя по теме. При этом учитель может больше внимания уделить индивидуальной работе с учениками. Таким образом, использование видеоурока способствует повышению эффективности традиционного урока.
Видеоурок начинается с объявления названия темы. Ученикам напоминается, что в ходе изучения геометрии они уже усвоили метод построения правильного треугольника, 4-угольника. Это простейшие фигуры, и для построения их достаточно было имеющихся знаний и умений. Отмечается, что при увеличении количества сторон правильного многоугольника, для его построения необходимо уметь построить для начала описанную около них окружность.

В начале видеоурока рассматривается пример построения правильного шестиугольника, длина стороны которого задана. Чтобы решить поставленную задачу, рекомендуется вспомнить формулу для вычисления стороны многоугольника, изученную на предыдущих уроках a6=2Rsin180°/6=2sin30°=2R·1/2=R. На рисунке к задаче строится отрезок PQ, который задает длину стороны шестиугольника. Для выполнения построения очерчивается окружность радиусом, равным заданному отрезку, длина которого равна длине стороны многоугольника, согласно формуле. На окружности отмечается произвольная точка А1. Таким же раствором циркуля на построенной окружности отмечаются точки от А2 до А6, расположенные друг от друга на расстоянии a6=R. Очевидно, что после соединения построенных точек отрезками А1А2=А2А3=А3А4=А4А5=А5А6, получаем искомый правильный шестиугольник А1А2А3А4А5А6.
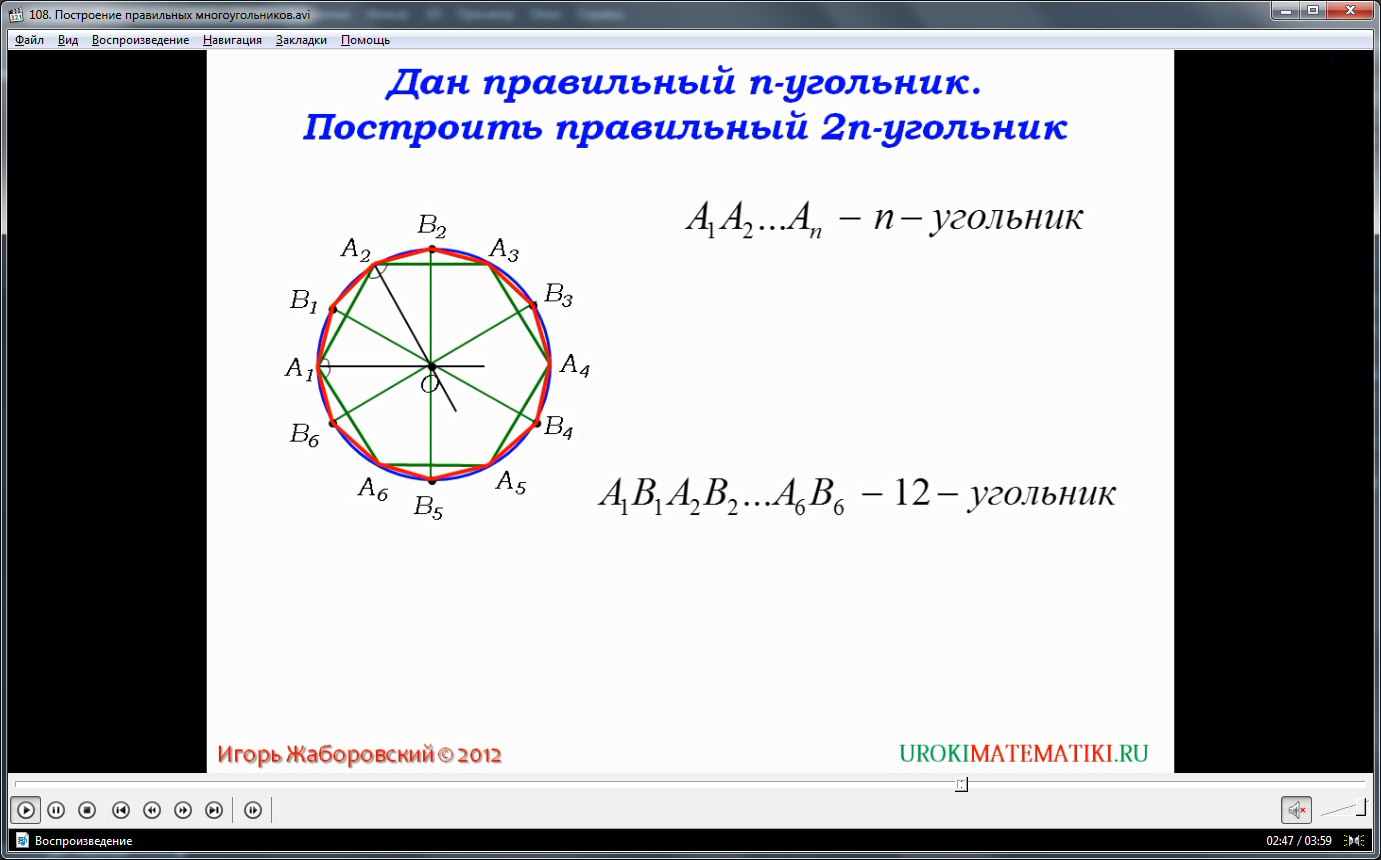
Отмечается, что в геометрии нередко необходимость построить правильный многоугольник возникает при решении задач с условием, где дан некоторый правильный n-угольник, а необходимо очертить правильный 2n-угольник. На рисунке дается построенный n-угольник. Чтобы произвести необходимое построение, очерчивается вспомогательная окружность, которая является описанной. Радиус такой окружности равен ОА1, а центр располагается в точке О. Затем от точки О через середину каждой стороны построенного многоугольника к соответствующей точке, делящей дугу окружности пополам, проводятся отрезки ОB1, OB2, и т.д. После построения соответствующих точек, они соединяются с вершинами А1, А2 и т.д. Таким образом, на рисунке из шестиугольника получилось построение 12-угольника А1 В1А2 В2А3 В3А4 В4А5 В5А6 В6. Отмечается, что аналогично с помощью простых инструментов - циркуля и линейки, строятся любые правильные многоугольники со сторонами 2k.
В конце видеоурока замечается, что многие правильные многоугольники строятся при помощи линейки, циркуля. Однако также замечется, что подобными построениями можно воспользоваться для очерчивания не всех правильных многоугольников. Примером такого многоугольника служит семиугольник, для построения которого недостаточно только этих инструментов. Однако при этом 17-угольник вполне может быть построен с помощью линейки и циркуля.
Видеоурок «Построение правильных многоугольников» может помочь повысить эффективность традиционного урока геометрии в школе. Также материал может быть использован в ходе дистанционного обучения. При необходимости ученику освоить учебную тему самостоятельно или углубить ее понимание, видео может быть рекомендовано для обучения дома.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6087 |
| Номер материала | 751 |