
Урок «Правила отыскания первообразных»

Краткое описание документа:
На прошлом занятии вы познакомились с новым видом взаимно-обратных действий: дифференцированием и интегрированием.
Дифференцирование — процесс нахождения производной функции, интегрирование — процесс нахождения функции по данной производной.
А так же узнали определение первообразной.
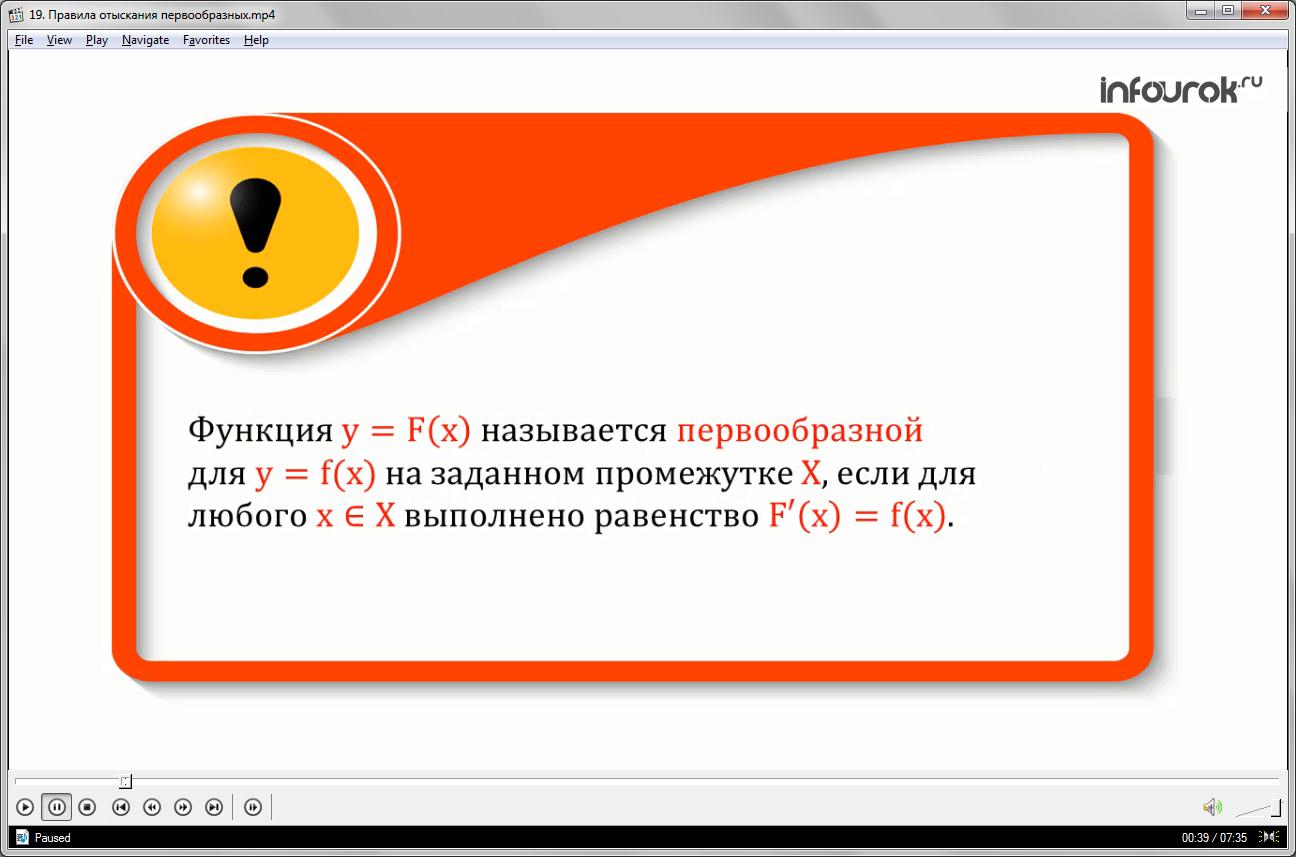
Функцию игрек, равное эф большое от икс, называют первообразной для функции игрек, равное эф малое от икс на заданном промежутке икс большое, если для любого икс, принадлежащего данному промежутку, выполнено равенство:
В процессе поиска первообразной функции возникает необходимость введения некоторых правил, с помощью которых можно найти данную первообразную.
Вы уже знаете, что производная суммы равна сумме производных — данное правило действительно и для первообразной суммы некоторых функций.
Итак, ПРАВИЛО 1:
Первообразная суммы равна сумме первообразных.
Например:
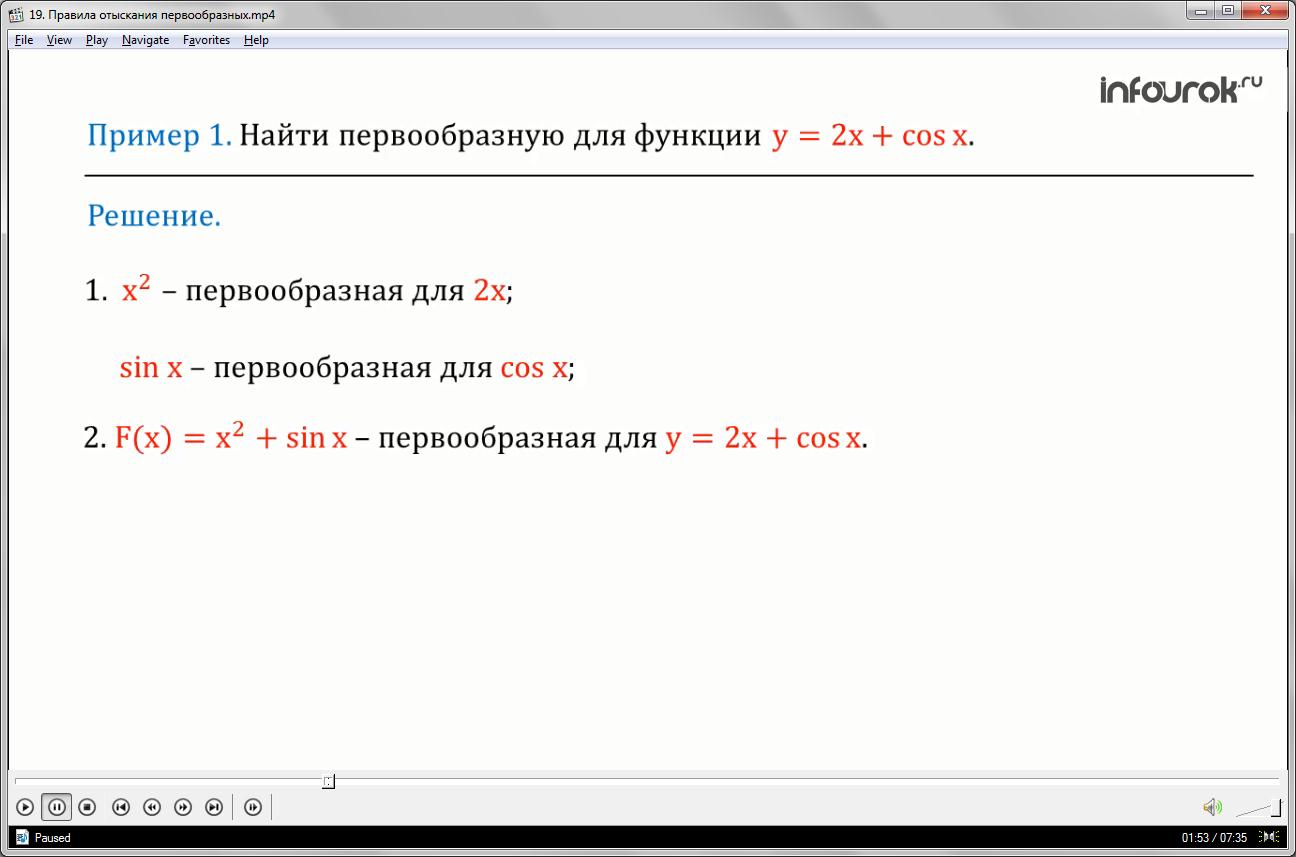
Найти первообразную для функции
Решение:
Не трудно понять, что первообразной для 2х служит функция х2, первообразной для служит .
По правилу суммы первообразных запишем:
Таким образом, для функции игрек равен два икс плюс косинус икс первообразной служит функция эф большое равно икс в квадрате плюс синус икс.
При нахождении производной постоянный множитель выносится за знак производной, данное правило действует и при нахождении первообразной.
Итак, ПРАВИЛО 2:
Постоянный множитель выносится за знак первообразной.
Рассмотрим пример:
Найти первообразную для функции (игрек равен минус три, делённое на два икс в квадрате).
Решение:
По определению степени с целым отрицательным показателем представим данную функцию в виде: (минус три вторых, умноженное на икс в минус второй степени).
По изученному выше правилу, постоянный множитель — минус три вторых — можно вынести за знак первообразной. Затем найдём первообразную от икс в минус второй степени по правилу нахождения первообразной степенной функции.
Получим: минус три вторых, умноженное на икс в минус первой степени, делённое на минус один. Сокращая минусы, имеем: минус три вторых, умноженное на икс в минус первой степени.
Запишем икс в минус первой степени в виде: один, делённое на икс, по определению степени с целым отрицательным показателем.
Мы получили первообразную: три, делённое на два икс, для функции минус три, делённое на два икс.
Известно, что производная произведения не равна произведению производных функций, аналогично, производная частного не равна частному от производных — данные правила более сложные.
Поэтому правил нахождения первообразных произведения и частного двух функций не существует.
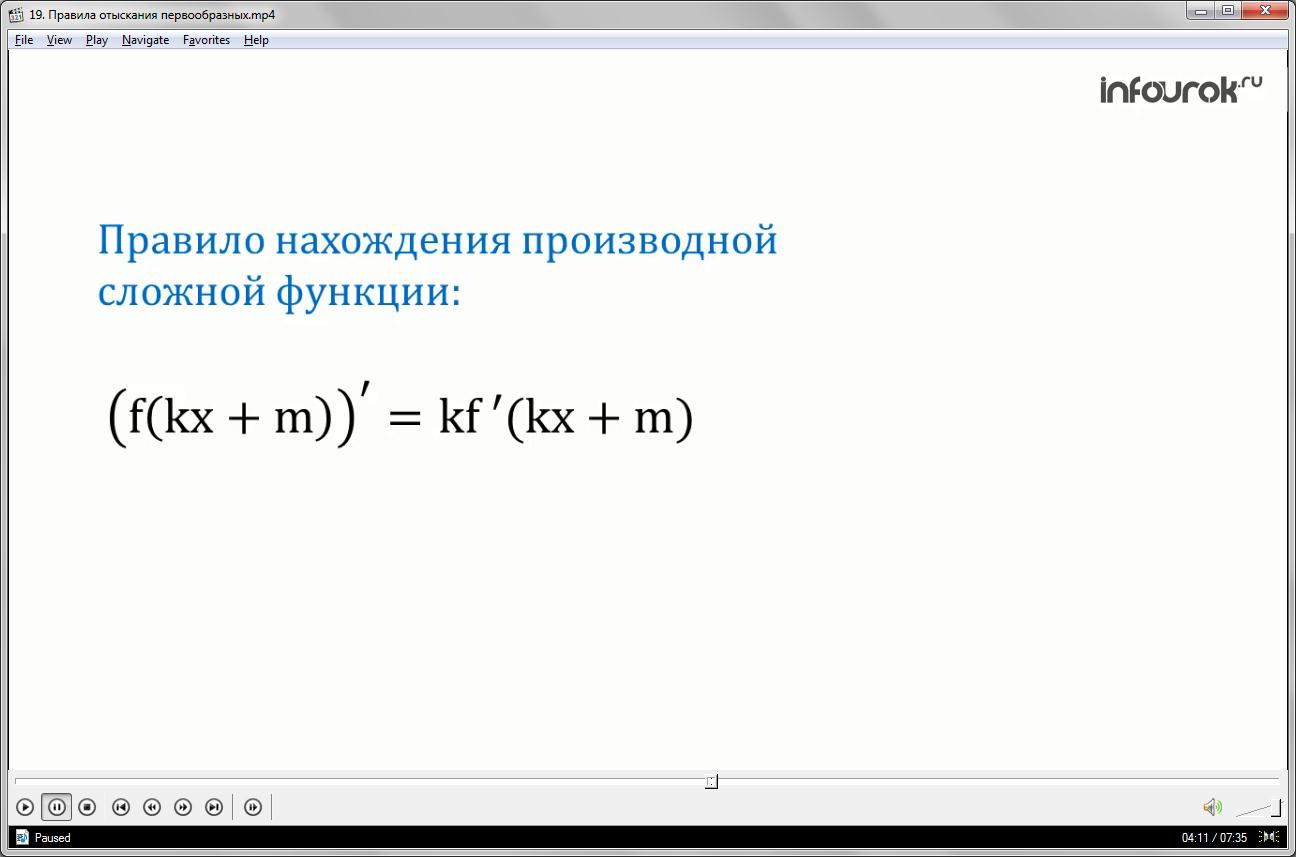
Вы знаете, что производная сложной функции эф от ка икс плюс эм вычисляется по формуле: ка, умноженное на производную эф от ка икс плюс эм.
Таким образом, можно ввести правило нахождения первообразной сложной функции.
Итак, ПРАВИЛО 3:
Если игрек, равное эф большое от икс — первообразная для функции эф малое от икс, то первообразной для функции игрек, равное эф малое от ка икс плюс эм, является функция игрек, равное один, делённое на ка, умноженное на эф большое от ка икс плюс эм.
Рассмотрим применение данного правила на примере.
Найти первообразную для функции игрек равен косинус икс, делённое на три.
Решение:
Постоянная при переменной икс равна одной третьей, значит один, делённое на ка равно трём.
Первообразной для косинуса икс, делённое на три, служит синус икс, делённое на три.
Подставим полученные данные в формулу для нахождения сложной функции, получим: три синус икс, делённое на три.
Таким образом, первообразной для функции игрек равен косинус икс, делённое на три, служит функция три синус икс, делённое на три.
Рассмотрим применение изученных правил при нахождении первообразной.
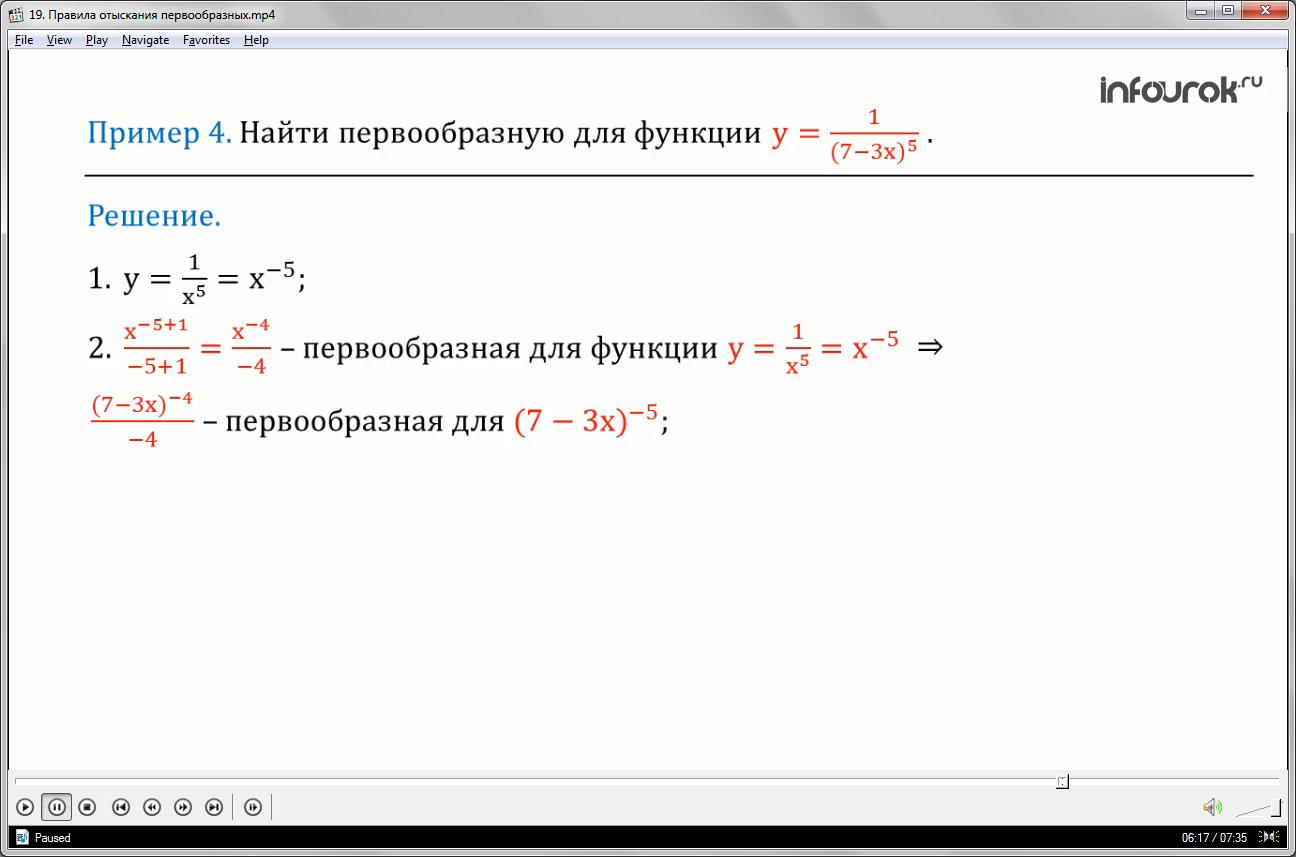
Найти первообразную для функции игрек равно один, деленное на семь минус три икс в пятой степени.
Решение:
1.Найдём первообразную для функции один, делённое на икс в пятой степени, для этого представим данное выражение в виде: икс в минус пятой степени (по определению степени с целым отрицательным показателем)
2.Первообразной для функции икс в минус пятой степени будет являться функция икс в минус четвёртой степени, делённое на минус четыре.
Значит, первообразной для функции игрек равно один, деленное на семь минус три икс в пятой степени, будет функция семь минус три икс — всё это в минус четвёртой степени и делённое на минус четыре, но этого ещё не достаточно, что бы утверждать, что задание решено.
3. Найдём первообразную для функции игрек равно один, деленное на семь минус три икс в пятой степени, с помощью формулы нахождения первообразной сложной функции .
Определим коэффициент при переменной икс, он равен минус три.
Подставим в данную формулу вместо ка — минус три, вместо эф большое от ка икс плюс эм подставим семь минус три икс — всё это в минус четвёртой степени и делённое на минус четыре.
Перемножим минус три и минус четыре, получим 12.
По определению степени с целым отрицательным показателем выражение семь минус три икс всё это в минус четвёртой степени запишем как один, делённое на семь минус три икс — всё это в четвёртой степени.
Таким образом, мы получили, что для функции
игрек равно один, деленное на семь минус три икс в пятой степени, первообразной является функция один, делённое на 12, умноженное на семь минус три икс — всё это в четвёртой степени.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4926 |
| Номер материала | 1068 |