
Урок "Предел числовой последовательности"

Краткое описание документа:
Видеоурок «Предел числовой последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии» предназначена для представления наглядного материала по данной теме. Учебный материал сложный и использование видеоурока для его наглядного представления повышает эффективность обучения, способствует более глубокому пониманию, запоминанию информации.
Наглядность обеспечивается с помощью инструментов, доступных для составления демонстрации в видео – анимационных эффектов, выделения цветом, вставка голосовых комментариев. Видео может применяться как наглядное пособие, а также в качестве части урока, заменяющей объяснение учителя. Это дает возможность уделить больше времени индивидуальной работе с учениками.
Демонстрация начинается с представления темы видеоурока и формулировки свойств сходящихся последовательностей. Указывается, что сходящаяся последовательность может сходиться только к одному пределу, а также то, что если последовательность сходящаяся, то это означает, что она ограничена. При этом также сообщается замечание, что ограниченная последовательность не обязательно должна быть сходящейся. Примером служит последовательность повторяющихся чисел -1, -2, -3, -1, -2, -3,… очевидно, что последовательность ограничена сверху и снизу, однако не сходится к некоторому числу. Отмечается, что необходимое условие сходимости последовательности было выделено немецким ученым Карлом Вейерштрассом, жившим в XIX веке. Это условие является третьим свойством сходящихся последовательностей, в котором указано, что последовательность сходящаяся, если она монотонная и ограниченная. Это утверждение называется теоремой Вейерштрасса.
Далее представляются важные пределы последовательностей, которые часто используются при решении задач – lim(1/n)=0 при n→∞ и lim qn=0 при n→∞ для числа |q|<1, а также постоянная последовательность lim С=С при n→∞. Также представляется теорема, которую необходимо знать для решения задач по данной теме, отображающую свойства пределов. Теорема утверждает, что для последовательностей, имеющих следующие пределы – lim xn=b при n→∞ и lim уn=с при n→∞, верны следующие свойства:
- Суммарный предел последовательностей равен сумме пределов lim (xn+уn)=b+с при n→∞.
- Предел произведения последовательностей определяется произведением пределов этих последовательностей lim xnуn=bс при n→∞.
- Для нахождения предела частного последовательностей нужно разделить пределы этих последовательностей, то есть lim (xn/уn)=b/с при n→∞.
- Если все члены последовательности имеют общий множитель, его можно вынести за знак предела, иначе lim kxn=kb при n→∞.
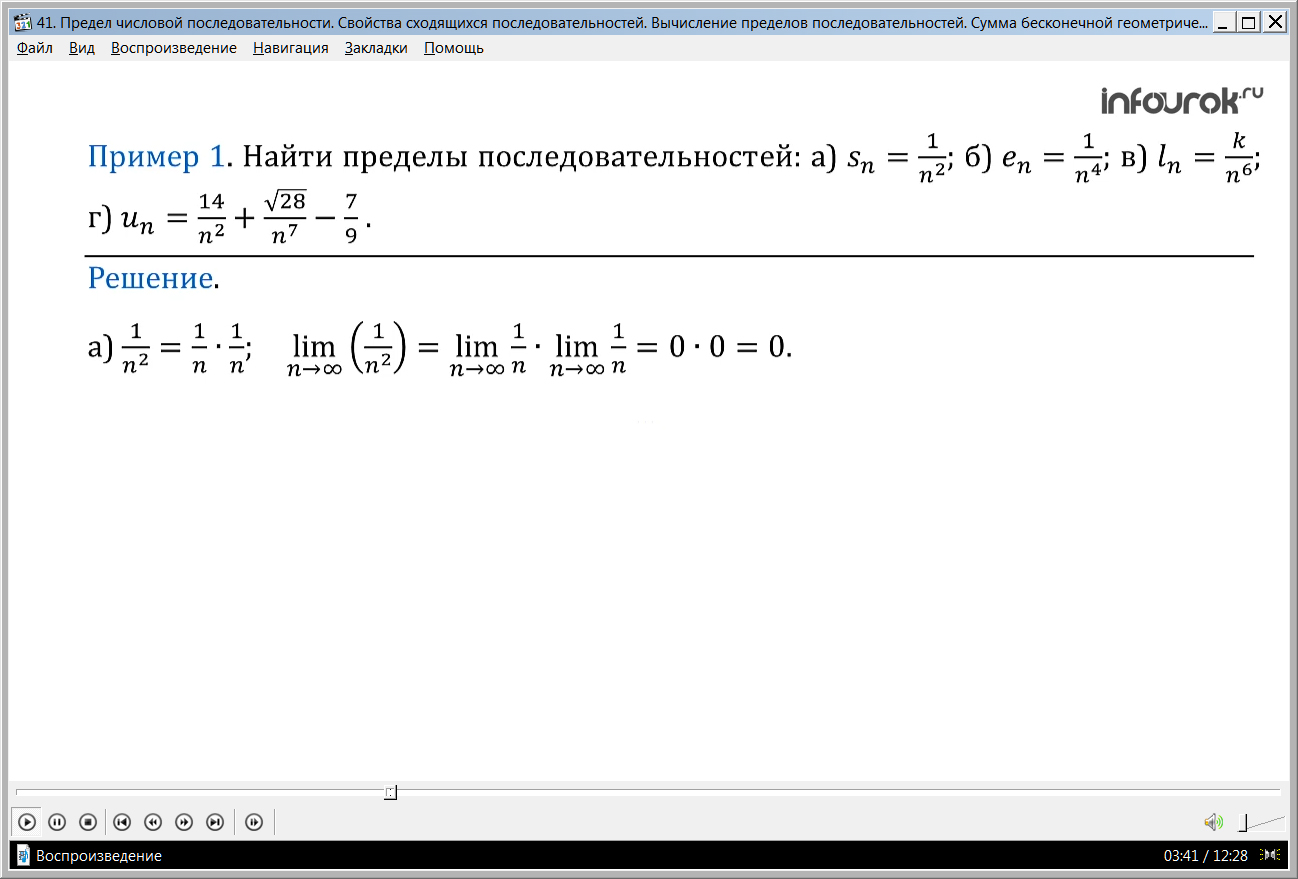
Далее рассматриваются примеры использование изученных свойств при решении задач. В первом примере необходимо найти пределы следующих последовательностей а)Sn=1/n2, б)en=1/n4, в)ln=k/n6, г)un=(14/n2)+(√28/n7)-7/9. Для решения примеров необходимо использовать известные пределы простых последовательностей и изученные свойства. В решении первого примера применяются знания о том, что предел последовательности lim 1/n=0 при n→∞. Используя свойство предела произведения последовательностей, находим lim 1/n2= lim((1/n)·(1/n))=0·0=0. Аналогично получаем значение предела в примере (б) lim 1/n4=0. Для решения примера (в) применяется свойство, в котором отмечается возможность выносить за знак предела постоянный множитель. Поэтому lim k/n6= k·lim 1/n6= k·0=0. Найденный предел рекомендуется запомнить как один из простейших пределов, применяемых для решения задач. При решении примера (г) используется свойство предела суммы последовательностей, а также пределов простых последовательностей 1/n и С. В результате вычисления получаем (14/n2)+(√28/n7)-7/9=-7/9.
Во втором примере дается геометрическая прогрессия Sn, для которой нужно вычислить предел. Отмечается, что последовательность описана формулой Sn=b1(qn-1)/(q-1). При этом b1≠0, а |q|<1. Так как b1 и q – это числа, то выражение b1/(q-1) можно вывести за знак предела. Остается найти b1/(q-1)lim(qn-1) при n→∞. Используя свойство предела разности последовательностей, находим lim(qn-1)= lim qn- lim 1. Так как q меньше единицы, то lim qn=0 при n→∞, а lim(qn-1)=-1. Результат вычисления предела всего выражения lim b1(qn-1)/(q-1)= b1/(1-q).
В примере 3 необходимо вычислить предел последовательности lim (√3n5-17)/(n5+9) при n→∞. Разделив числитель и знаменатель дроби на высшую степень переменной, получаем lim (√3-17/ n5)/(1+9/n5). Применив свойство предела частного последовательностей, находим предел числителя и знаменателя. В итоге получаем предел частного √3.
Далее рассматривается сумма геометрической прогрессии b1, b2, b3, …, bn,…. Расписываются суммы членов последовательности S1=b1, S2=b1 +b1 и т.д., получая новую последовательность S1 , S2 и т.д. Отмечается, что последовательность может сходиться или расходиться. Число S будет суммой геометрической последовательности, если последовательность Sn сходится к числу S. Если последовательность не расходится, то сумму можно найти, но о ней не говорят. Для знаменателя |q|<1 сумма геометрической прогрессии Sn= b1(qn-1)/(q-1). Устанавливается связь между найденным пределом геометрической прогрессии, найденным во втором примере, и суммой геометрической прогрессии. Сообщается, что это одно и тоже число. На экран выводится правило, что для геометрической прогрессии со знаменателем |q|<1, для вычисления суммы используется формула Sn=b1/(1-q).
В примере 4 описывается решение задания, где требуется найти сумму геометрической прогрессии 12, 6, 3, 3/2, ¾,… В данной геометрической прогрессии b1=12, а q=1/2. Для нахождения суммы геометрической прогрессии, где |q|<1, используется формула Sn=b1/(1-q). Подставив значения, получаем сумму Sn=24.
Пример 5 описывается решение задания, в котором требуется найти третий член прогрессии, для которой известна сумма геометрической прогрессии, равная 18, сумма квадратов ее членов, равная 64,8. Для решения используется формула суммы геометрической прогрессии с |q|<1. Подставив в нее известное значение, получаем уравнение b1/(1-q)=18. Для последовательности возведенных в квадрат членов последовательности b12/(1-q2)=64,8. Есть два уравнения с двумя неизвестными. Решив их, получаем значения b1=6 и q=2/3. Третий член последовательности находится, подставив значения в формулу b3= b1q2=8/3.
Видеоурок «Предел числовой последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии» может применяться на традиционном школьном уроке для повышения его эффективности. Также пособие может быть полезно учителю, объясняющему тему дистанционно. Ученикам, недостаточно хорошо освоившим тему, можно рекомендовать видеопособие для самостоятельного рассмотрения.
ТЕКСТОВАЯ РАСШИФРОВКА:
ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
2. Свойства сходящихся последовательностей
Свойство 1. Если последовательность сходится, то только к одному пределу.
Свойство 2. Если последовательность сходится, то она ограниченна.
Замечание: Если последовательность ограниченна, то она не обязательно сходится.
Пример, –1,– 2,– 3, –1, –2, –3,..., –1, –2, –3,... – ограниченная последовательность, но она не сходится.
Необходимое и достаточное условие сходимости последовательности доказал в XIX в. немецкий математик Карл Вейерштрасс. Оказывается, если последовательность не только ограниченна, но и монотонна (убывает или возрастает), то она обязательно сходится, это и есть третье свойство сходимости.
Свойство 3. Если последовательность монотонна и ограниченна, то она сходится (теорема Вейерштрасса).
3. Вычисление пределов последовательностей
К установленным ранее двум важным результатам:
1) ; ( предел единицы, деленной на эн, при стремлении п к бесконечности равен нулю)
2) , если |q|<1, ( предел ку в степени эн при стремлении п к бесконечности равен нулю, если модуль ку меньше единицы)
Иными словами, предел постоянной последовательности равен значению этой постоянной.
Для вычисления пределов последовательностей в более сложных случаях используются указанные соотношения и следующая теорема.
Теорема. Если (предел икс энного равен бэ), , (предел игрек энного равен цэ) то:
1) предел суммы равен сумме пределов:
2) предел произведения равен произведению пределов:
3) предел частного равен частному от деления пределов:
при условиях: c0(це не равно нулю) иyn0 (игрек энный не равен нулю)для любого n (эн);
4) постоянный множитель можно вынести за знак предела:
k– любое число, k0 (ка не равно нулю).
Пример 1. Найти пределы последовательностей: а) (эс энное равно единица деленное на эн в квадрате); б) ; (е энное равно единица, деленная на эн в четвертой степени);
в) ;( эль энное равно ка, деленое на эн в шестой степени);
г) (у энное равно 14, деленное на эн в квадрате, плюс корень из 28-ми, деленное на эн в седьмой степени, минус семь девятых).
Решение. а) Имеем: =·(один деленное на эн в квадрате, равно произведению дробей единица, деленная на эн). Применив правило «предел произведения», получим: (предел единицы, деленной на эн в квадрате, равно произведению пределов дробей единица, деленная на эн, равно нуль умножить на нуль равно нулю).
б) Рассуждая, как в п. а), получим: (предел единицы, деленное на эн в четвертой равен нулю).
в) (предел ка, деленое на эн в шестой степени равен предел ка, умноженное на дробь единица, деленная на эн в шестой степени, равно ка умножить на предел единица, деленная на эн в шестой степени равно ка умножить на нуль равно нуль).
Вообще, для любого натурального показателя т (эм) и любого коэффициента k (ка) справедливо соотношение: .
г) Применив правило «предел суммы», получим:
(Предел суммы равен сумме пределов, где первый и второй пределы равны нулю, а третий предел постоянного числа равен числу семь девятых, в результате получили минус семь девятых).
Пример 2. Даны числа b1 и q (бэ первое и ку), такие, что b10, |q|< 1. (бэ первое не равно нулю, модуль ку меньше единицы). Вычислить (предел эс энное), где (эс энное равно дроби в числителе бэ первое, умноженное на ку в энной минус один, в знаменателе ку минус один).
Решение. Прежде всего воспользуемся тем, что постоянный множитель можно вынести за знак предела. Получим:
(предел эс энное равно бэ первое, деленное на ку минус один, умноженное на предел ку в энной минус один).
Далее воспользуемся тем, что (предел ку в энной равен нулю) и, следовательно, (предел ку в энной минус один равен минус одному).
( бэ первое, деленное на ку минус один, умноженное на предел ку в энной минус один равно бэ первое, деленное на один минус ку).
Ответ: .(предел эс энное равен бэ первое, деленное на один минус ку).
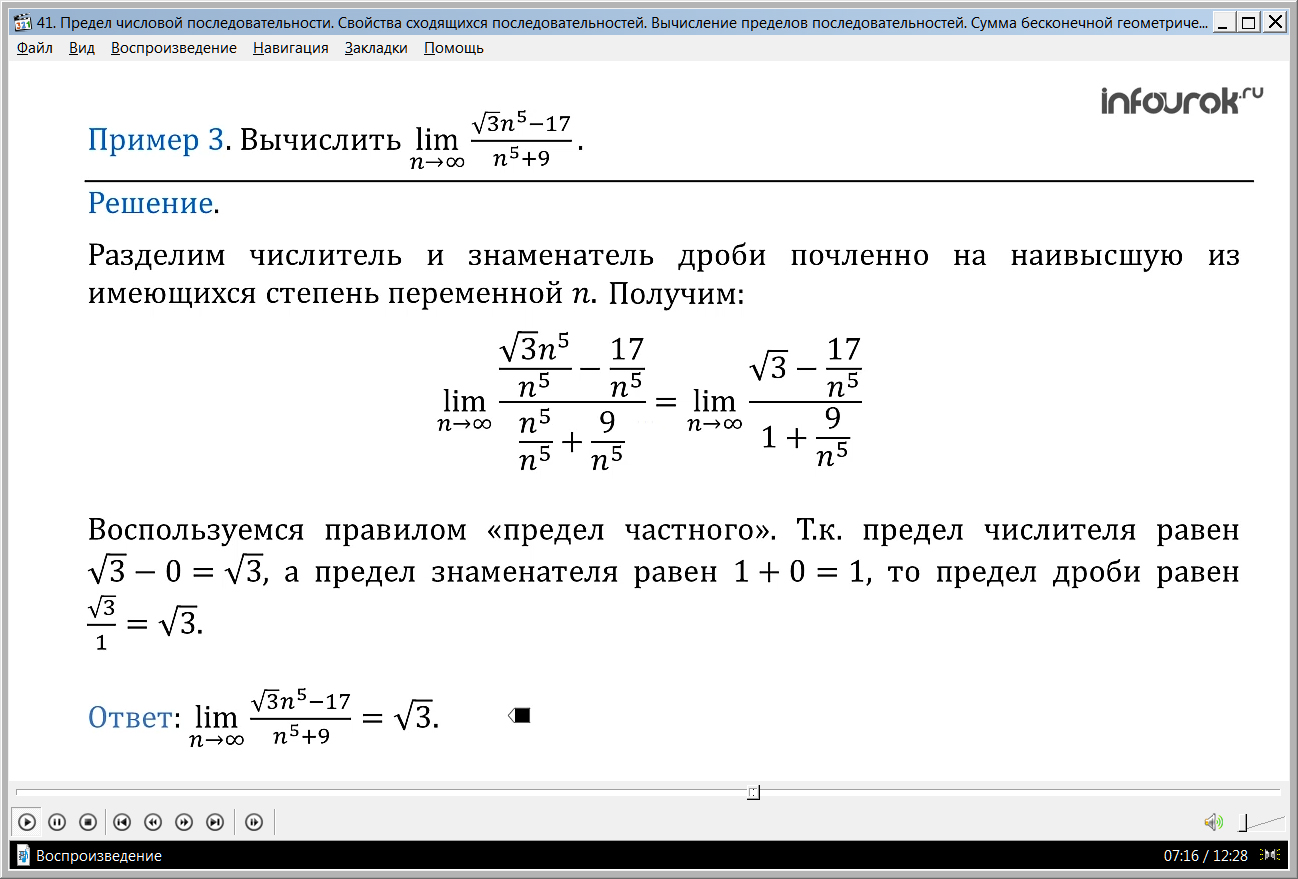
Пример 3. Вычислить (предел дроби в числителе корень из трех эн в пятой минус 17 в знаменателе эн в пятой плюс 9)
Решение. В подобных случаях применяют искусственный прием: делят и числитель, и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n(эн). В данном примере разделим числитель и
знаменатель дроби почленно на n5. Получим:
Далее воспользуемся правилом «предел частного». Поскольку предел
числителя равен – 0=, а предел знаменателя равен 1+0 = 1, то предел
дроби равен .
4. Сумма бесконечной геометрической прогрессии
Рассмотрим бесконечную геометрическую прогрессию:
b1, b2, b3, ..., bn, ... (бэ первое, бэ второе, бэ третье и так далее бэ энное и так далее)
Будем последовательно вычислять суммы двух, трех, четырех и
т.д. членов прогрессии:
S1= b1; (эс первое равно бэ первое)
S2= b1+b2; (эс второе равно бэ первое плюс бэ второе)
S3 =b1+b2+b3;
S4 =b1+b2+b3+b4;
…
Sn =b1+b2+b3+...+bn. (эс энное равно бэ первое плюс бэ второе плюс бэ третье плюс и так далее плюс бэ энное)
Получилась последовательность S1, S2, S3,..., Sn,... (эс первое эс второе эс третье и так далее эс энное и так далее). Как всякая числовая последовательность, она может сходиться или расходиться. Если последовательность Sn (эс энное) сходится к пределу S,(эс) то число S называют суммой геометрической прогрессии (обратите внимание: не суммой nчленов геометрической прогрессии, а суммой всей геометрической прогрессии). Если же эта последовательность расходится, то о сумме геометрической прогрессии не говорят, хотя сумму n членов геометрической прогрессии можно найти и в этом случае.
Предположим, что знаменатель q геометрической прогрессии
удовлетворяет неравенству |q|< 1. (модуль ку меньше одного)
Напомним формулу суммы первых n членов геометрической прогрессии: если Sn = b1+b2+b3+...+bn, (эс энное равно бэ первое плюс бэ второе плюс бэ третье плюс и так далее плюс бэ энное), тo . (эс энное равно дроби: в числителе бэ первое, умноженное на ку в энной минус один, в знаменателе ку минус один).
Во втором примере мы установили, что ( предел эс энное равен бэ первое, деленное на один минус ку). Но (предел эс энное) мы назвали выше суммой геометрической прогрессии. Таким образом, мы доказали следующее утверждение:
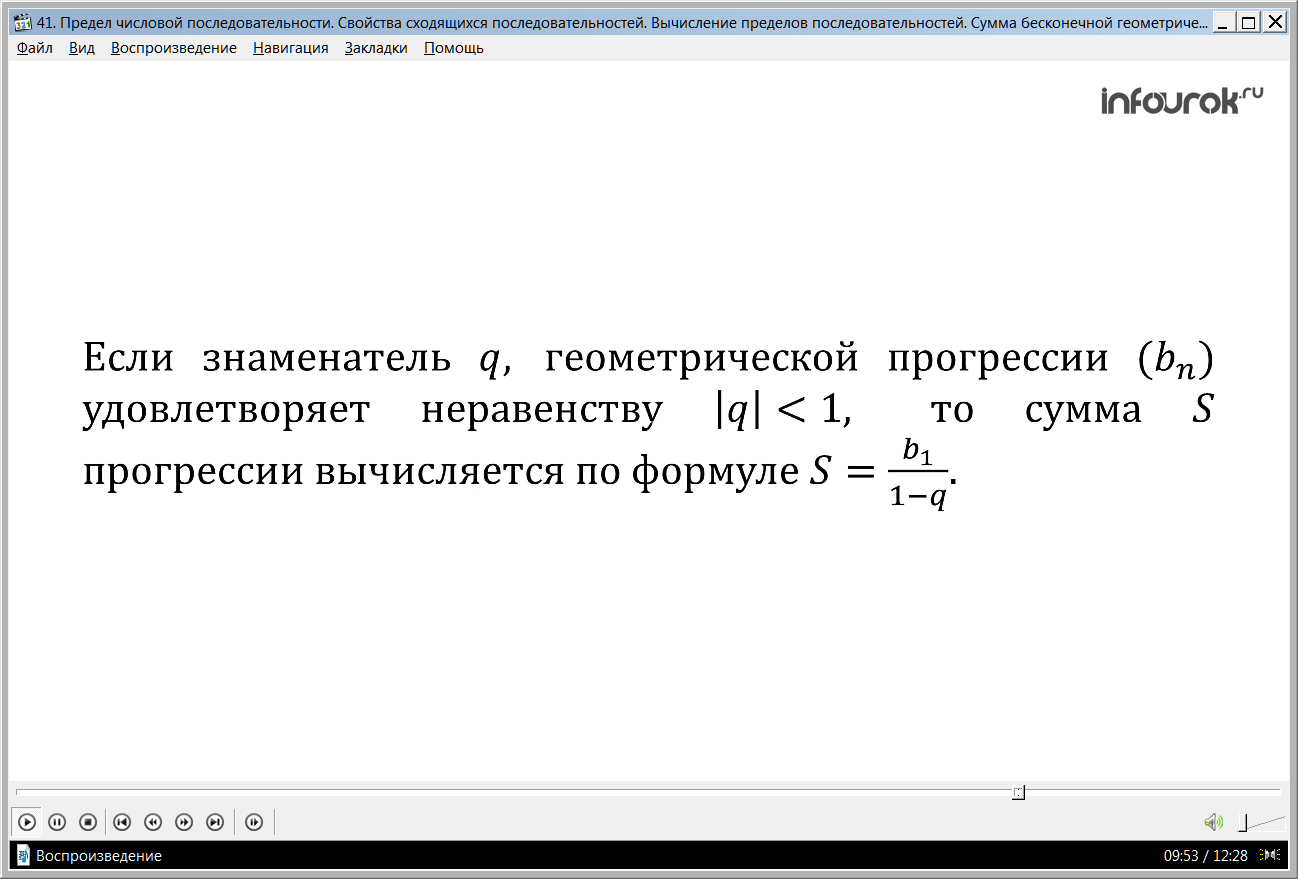
Если знаменатель q (ку) геометрической прогрессии (bn) (бэ энное) удовлетворяет неравенству |q|<l, (модуль ку меньше одного), то сумма S (эс) прогрессии вычисляется
по формуле . (эс равно бэ первое, деленное на один минус ку).
Пример 4. Найти сумму геометрической прогрессии: 12, 6, 3, , , …
Решение. Имеем: b1 =12, q =(бэ первое равно 12, ку равно одной второй). Поскольку знаменатель прогрессии удовлетворяет неравенству |q|< 1(модуль ку меньше одного), мы вычислим сумму прогрессии по формуле . Значит, сумму геометрической прогрессии равна 24 ( ).
Ответ: S = 24.
Пример 5. Сумма геометрической прогрессии равна 18, а сумма квадратов ее членов 64,8. Найти третий член прогрессии.
Решение. Первый этап. Составление математической модели. Дана геометрическая прогрессия: b1, b2, b3, ..., bn, ... со знаменателем q(|q|<l)(ку), ее сумма вычисляется по формуле S=. По условию эта сумма равна S=18. Таким образом, получаем уравнение .
Последовательность , , , ..., , ... также является геометрической прогрессией: ее первый член равен , знаменатель равен q2, а сумма вычисляется по формуле S2=. По условию эта сумма равна S2 =64,8. Таким образом, получаем уравнение
Что выделено желтым только писать на экране.
В итоге задача сводится к решению системы уравнений относительно
переменных b1 и q: (бэ один и ку)
Второй этап. Работа с составленной моделью.
Для решения системы используем метод подстановки: выразим из первого уравнения переменную b1,(бэ один). Получим b1 = 18(1– q). Подставим это выражение вместо b1 во второе уравнение системы. Получим:
Далее последовательно находим q (ку) и b1 (бэ один)
Итак,
5-5q=1+q; q= =
b1=18(1–)=6
Третий этап. Ответ на вопрос задачи.
По условию требуется найти b3.(бэ третье) Имеем: b3 =b1q2 =6 = . ( бэ третье равно восемь третьих).
Ответ: b3
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5509 |
| Номер материала | 864 |