
Урок "Предел числовой последовательности. Определение предела последовательности"

Краткое описание документа:
Видеоурок «Предел числовой последовательности. Определение предела последовательности» будет являться отличным сопровождением при изучении данной темы из области тригонометрии, которой уделяется огромное внимание 10 классе. Данному разделу посвящается большое количество уроков по той причине, что тригонометрия является актуальной при решении задач по алгебре, геометрии, физике, механике и прочее.
При решении задач, которые возникают в различных областях могут появляться последовательности различной сложности, которые будут обладать уникальными свойствами и характеристиками. Этот видеоурок, как и предыдущий, посвящен изучению последовательностей. В предыдущем уроке диктор рассказал, что такое последовательность, какими она может быть, какие существуют способы ее представления. Рассматривались также свойства монотонности и ограниченности последовательностей.
В этом видеоуроке будет рассматриваться такое понятие, как предел последовательности. В первую очередь на экран выводится некоторая возрастающая последовательность, каждый элемент которой представляет собой квадрат некоторого числа, на единицу больше, предыдущего. Данная последовательность является монотонной. Она не может иметь предела, ведь не ограничена сверху.
Вторая же последовательность, которая приводится ниже, представляет собой дроби с числителем, равным 1, и знаменателями, которые представляют собой множество простых чисел. Таким образом, вторая последовательность является убывающей. Это можно легко понять, ведь каждый последующий элемент является меньше предыдущей. Это связано с тем, что числители всех элементов являются одинаковыми, а знаменатели – увеличиваются. Чем больше знаменатель, тем меньше дробь.
Данные числовые последовательности демонстрируются геометрическим образом на единичной числовой оси. Во втором случае легко заметить, что имеется значение, при котором все элементы последовательности являются меньше него. Это говорит о том, что последовательность сама по себе является ограниченной сверху, согласно определению, изученному в предыдущем уроке.
Иными словами можно сказать так: первая последовательность расходится, а вторая – сходится. Эти термины довольно часто будут встречаться в дальнейшем при изучении последовательностей и пределов последовательностей.
Если взять некоторую точку из последовательности, то практически всегда можно рассмотреть ее окрестность. Об этом говориться далее в видеоуроке. Также рассматривается понятие радиуса окрестности. Для того чтобы школьники могли увидеть это наглядно, данное понятие демонстрируется на единичной координатной оси. Радиус окрестности, также как и радиус окружности, принято обозначать через маленькую латинскую букву r.
Приводится пример интервала некоторой окрестности для точки 7, радиус окрестности которого равняется 0,03. Нетрудно догадаться, что это совсем небольшой интервал, однако, в некоторых случаях придется работать и с подобными интервалами.
Понятие окрестности точки необходимо было рассмотреть для того, чтобы в дальнейшем дать определение понятию предел. Он условно обозначен латинской маленькой буквой b. Диктор подробно комментирует и объясняет данное определение. Учитель может предложить ученикам записать его в тетради. Для того чтобы его запомнить, необходимо продемонстрировать его на практических примерах, с помощью чего оно запомниться школьникам на долгое время.
Ниже от определения приводится алгебраическая запись понятия «предел», его обозначение (через сокращенное lim либо стрелочку, напоминающую знак следствия).
Далее диктор приводит пояснения к ранее выведенному определению, после чего рассматривается некоторое замечание. Очень важно понять суть этого замечания, чтобы уловить смысл предела последовательности.
После этого приводится первый практический пример. В ней рассматривается некоторая последовательность отрицательных дробных чисел. Необходимо доказать, что данная последовательность стремиться к нулю, то есть ее предел равняется нулю. При доказательстве опираемся на ранее изученное определение окрестности некоторой точки. Данное решение можно рассмотреть также вместе с учителем либо репетитором. Если школьники поймут суть понятия, то им намного проще будет в дальнейшем находить пределы и доказывать аналогичные примеры.
Второй пример предлагает найти предел некоторой последовательности. Решение также приводится подробным и последовательным образом, что очень важно. Диктор не упускает при объяснении ни один важный момент.
Если некоторая последовательность не имеет предела, иногда говорят что она «не имеет точки сгущения».
После рассмотрения еще одного примера, приводятся графические объяснения понятия предела. Мы видим, что предел графически представляет себя прямую, к которой стремиться график, но не пересекает, иными словами – горизонтальную асимптоту.
Для того чтобы уметь справляться с различными тригонометрическими уравнениями, сложными и простыми выражениями, необходимо изучить не только основные тригонометрические уравнения, но и некоторые другие их следствия. При их изучении важно понять принцип их получения. При этом запоминание во многом упроститься. Если решить достаточное количество практических заданий можно с легкостью распознать, где и какие формулы необходимо использовать. Таким образом, у школьников появятся еще одни необходимые навыки в области тригонометрии.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим две числовые последовательности (уn) (игрек энная) и (хn) (икс энная). (уn): 1, 4, 9, 16, 25, ..., n2, ...;
(xn)
Изобразив члены этих последовательностей точками на координатных прямых для (уn) (игрек энной) (рис 1)и для (хn) (икс энной) (рис 2). Видим, что у первой последовательности (уn) (игрек энной) точки удаляются, то есть нет «точки сгущения», а члены второй последовательности (хn) (икс энной) «сгущаются» около точки 0. В подобных случаях математики говорят так: последовательность (хn) (икс энная) сходится, а последовательность (уn) (игрек энная) расходится.
Возникает вопрос: как узнать, является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности. Чтобы ответить на этот вопрос, введем новый математический термин.
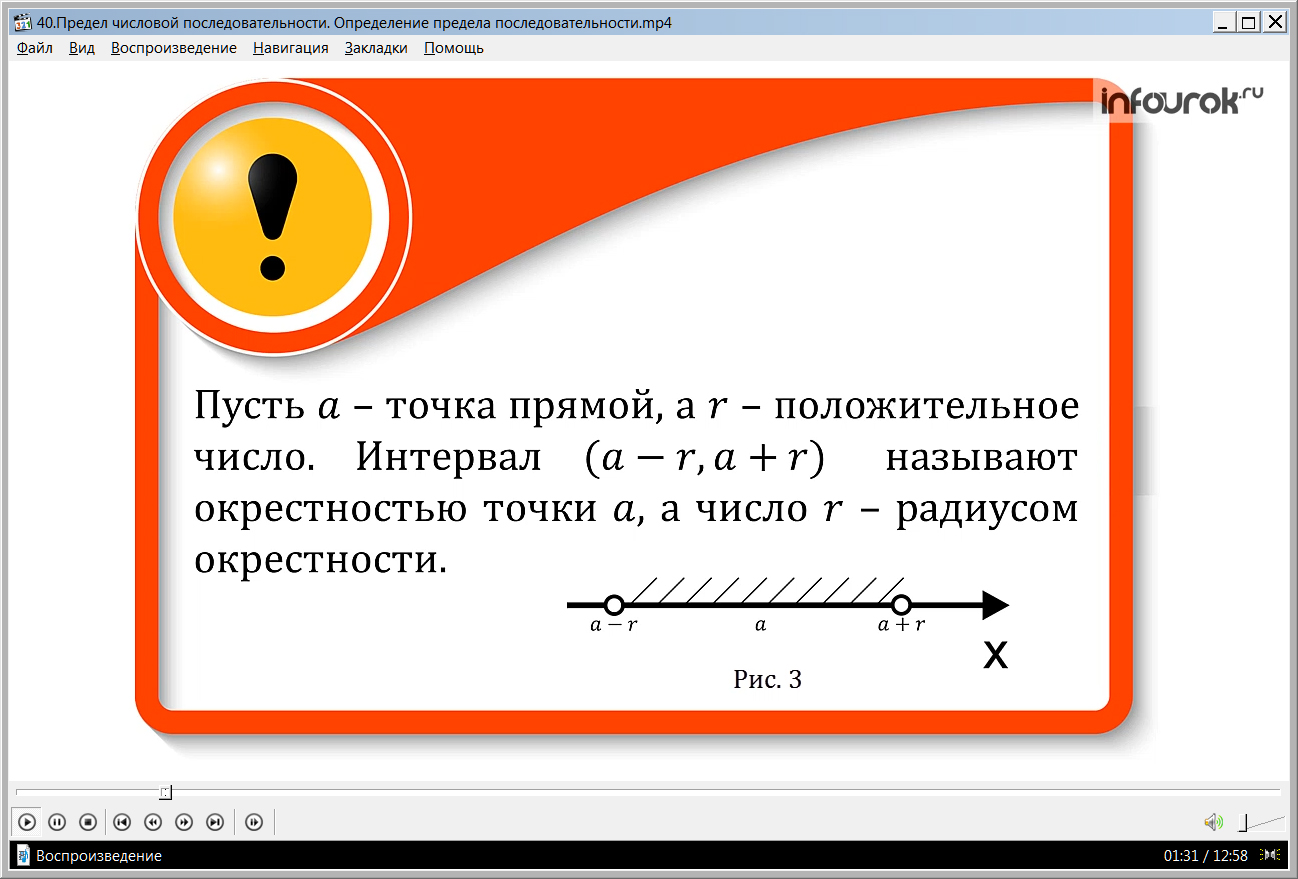
Определение 1. Пусть а – точка прямой, а r— положительное число. Интервал (а–r, а+r)(от а минус эр до а плюс эр)называют окрестностью точки а (рис. 3), а число r – радиусом окрестности.
Рис. 3
Пример,
Интервал (6,97; 7,03) (от шести целых девяноста семи сотых до семи целых трех сотых)– окрестность точки 7, причем радиус этой окрестности равен 0,03.
Ответим на поставленный выше вопрос. Но уточним: математики вместо термина «точка сгущения для членов заданной последовательности», используют термин «предел последовательности».
Определение 2. Число b называют пределом последовательности (уn) (игрек энная), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера.
Пишут либо так: уn b (читают: уn(игрек энный) стремится к b или уn сходится к b), либо так: (читают: предел последовательности уn(игрек энной) при стремлении n к бесконечности равен b; но обычно слова «при стремлении n к бесконечности» опускают).
Поясним определение предела последовательности.
Пусть . (предел последовательности уn(игрек энной) при стремлении n к бесконечности равен b).
Возьмем интервал (b–r1, b+r1) (от бэ минус эр первое до бэ плюс эр первое), т.е. окрестность точки b(бэ); r1 (эр первое)— радиус этой окрестности (r1 >0) (эр первое больше нуля). Существует номер n1 (эн первый), начиная с которого вся последовательность содержится в указанной окрестности: (b–r1, b+r1), (b–r1, b+r1), (b–r1, b+r1),и т.д. (игрек эн первый принадлежит интервалу от бэ минус эр первое до бэ плюс эр первое, игрек эн первый плюс один принадлежит интервалу от бэ минус эр первое до бэ плюс эр первое и т.д.) (номера членов последовательности начинаются с n1, следующий n1+1 …)
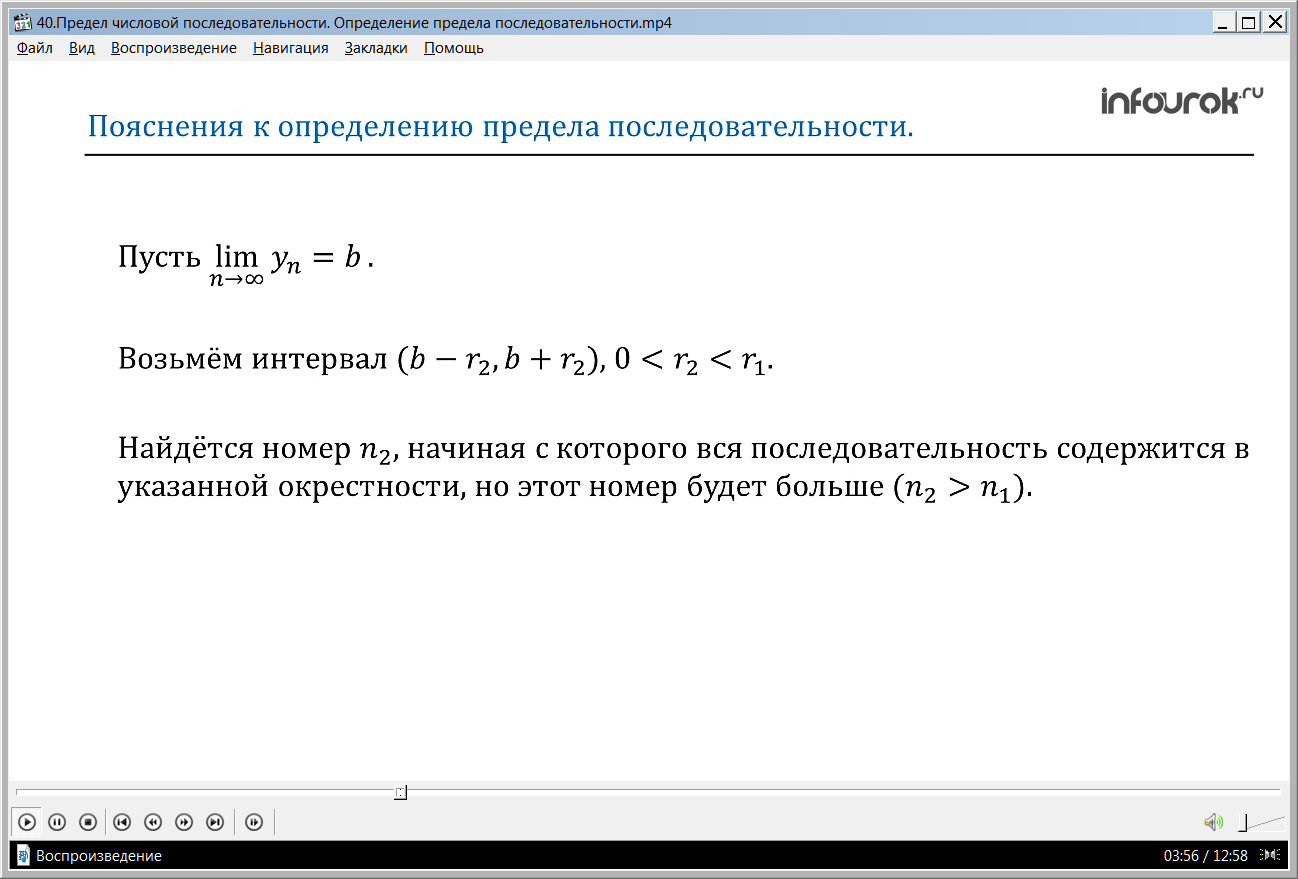
А что будет, если взять интервал (b–r2, b+r2) (от бэ минус эр второе до бэ плюс эр второе), где 0 <r2 <r1, (эр второе больше нуля, но меньше эр первого) т.е. если уменьшить радиус окрестности? Опять найдется номер n2, начиная с которого вся последовательность содержится в указанной окрестности, но этот номер будет больше, т.е. n2 >n1. (эн второй больше эн первого)
Замечание. Если число b — предел последовательности (yn) (игрек энной), то, окрестность точки b– это «отрезок», для последовательности: куда попадают члены последовательности, начиная с некоторого номера n0 (эн нулевого), то есть (игрек эн нулевой) и все последующие члены последовательности. Чем «меньше» отрезок, т.е. чем меньшая выбирается окрестность, тем больше членов последовательности остаются вне него, но потом все равно попадают в выбранную окрестность.
Пример 1. Дана последовательность (хn) (икс энная):
(минус один, минус одна вторая, минус одна третья, минус одна четвертая и так далее минус один, деленное на эн и так далее)
Доказать, что .
Решение. Возьмем любую окрестность точки 0, пусть ее радиус равен r
(рис. 3). Ясно, что всегда можно подобрать натуральное число n0 (эн нулевое) так, чтобы выполнялось неравенство , т.к. у нас члены последовательности приближаются к нулю слева, то они должны быть больше минус эр. Если, например, r = 0,0001, то в качестве n0 можно взять 10001, поскольку – >–0,0001; если r=, то в качестве n0 можно взять 5774, поскольку –>–, и т.д. Но это значит, что член последовательности уn(игрек энной) с номером n0 (эн нулевое), т.е. (игрек эн нулевой), попадает в выбранную окрестность точки 0. Тем более в этой окрестности будут находиться все последующие члены заданной возрастающей последовательности . В соответствии с определением 2 это и означает, что (предел последовательности минус единица, деленная на эн, при стремлении эн к бесконечности равен нулю).
Аналогично рассматривается пример о нахождении предела последовательности уn= и равен он также нулю , т.е.
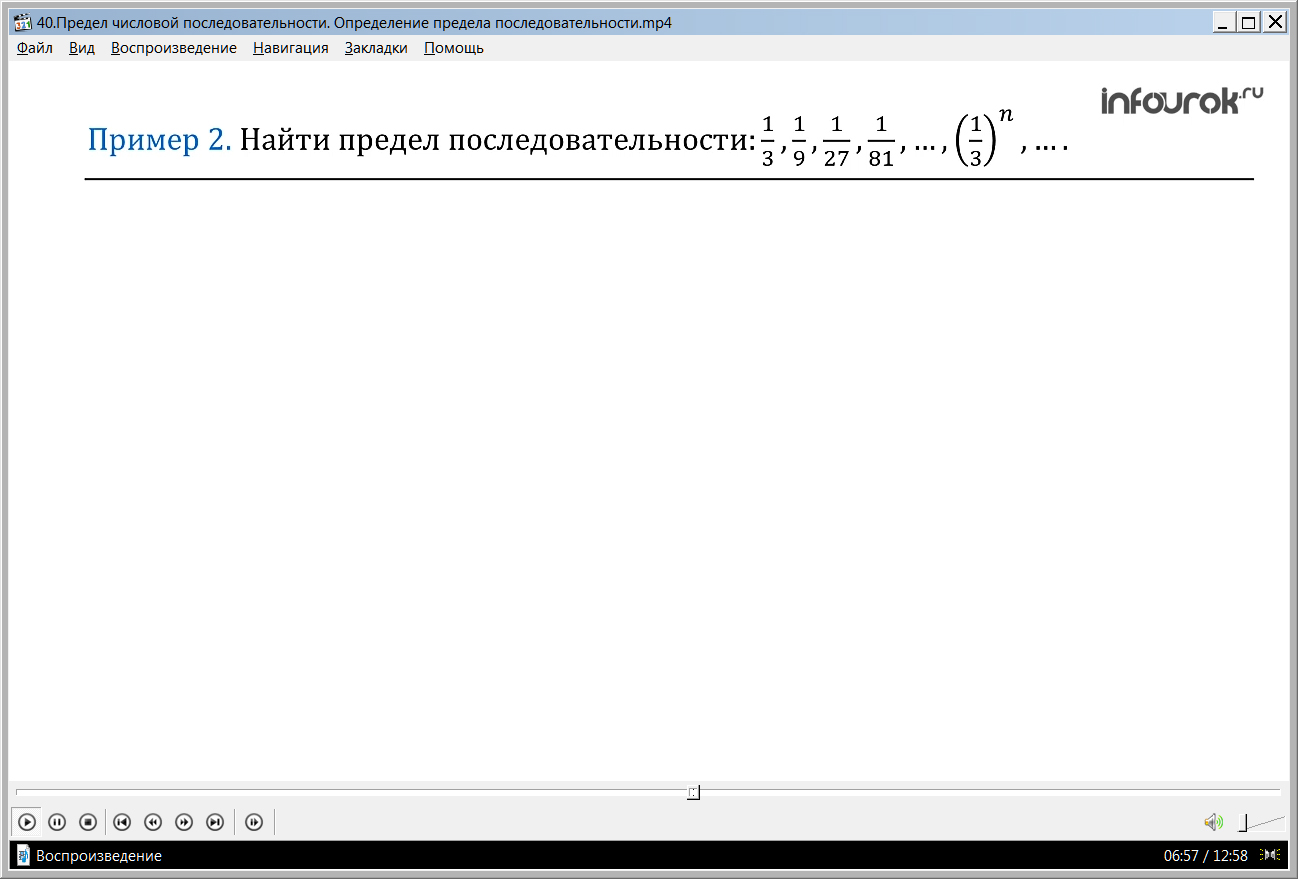
Пример 2. Найти предел последовательности: , , , , …, , …
Решение. Здесь, как и в предыдущем примере, последовательность сходится к 0: (одна третья в энной степени стремиться к нулю) или (предел последовательности одной третьей в энной степени при стремлении эн к бесконечности равен нулю).
Результат, полученный в данном примере, является частным случаем более общего утверждения :
ВЫВОД: если |q|<l (модуль ку меньше единицы), то . (предел последовательности ку в энной степени при стремлении эн к бесконечности равен нулю).
А что будет с последовательностью qn(ку в энной степени), если|q|>1(модуль ку больше единицы)?
Пусть, q =5, т.е. речь идет о последовательности 5, 52, 53, 54, ..., 5n, ...
Эта последовательность явно не имеет предела (нет «точки сгущения»). Вообще, справедливо утверждение:
ВЫВОД: если |q|>1(модуль ку больше единицы), то последовательность qn(ку в энной степени) расходится.
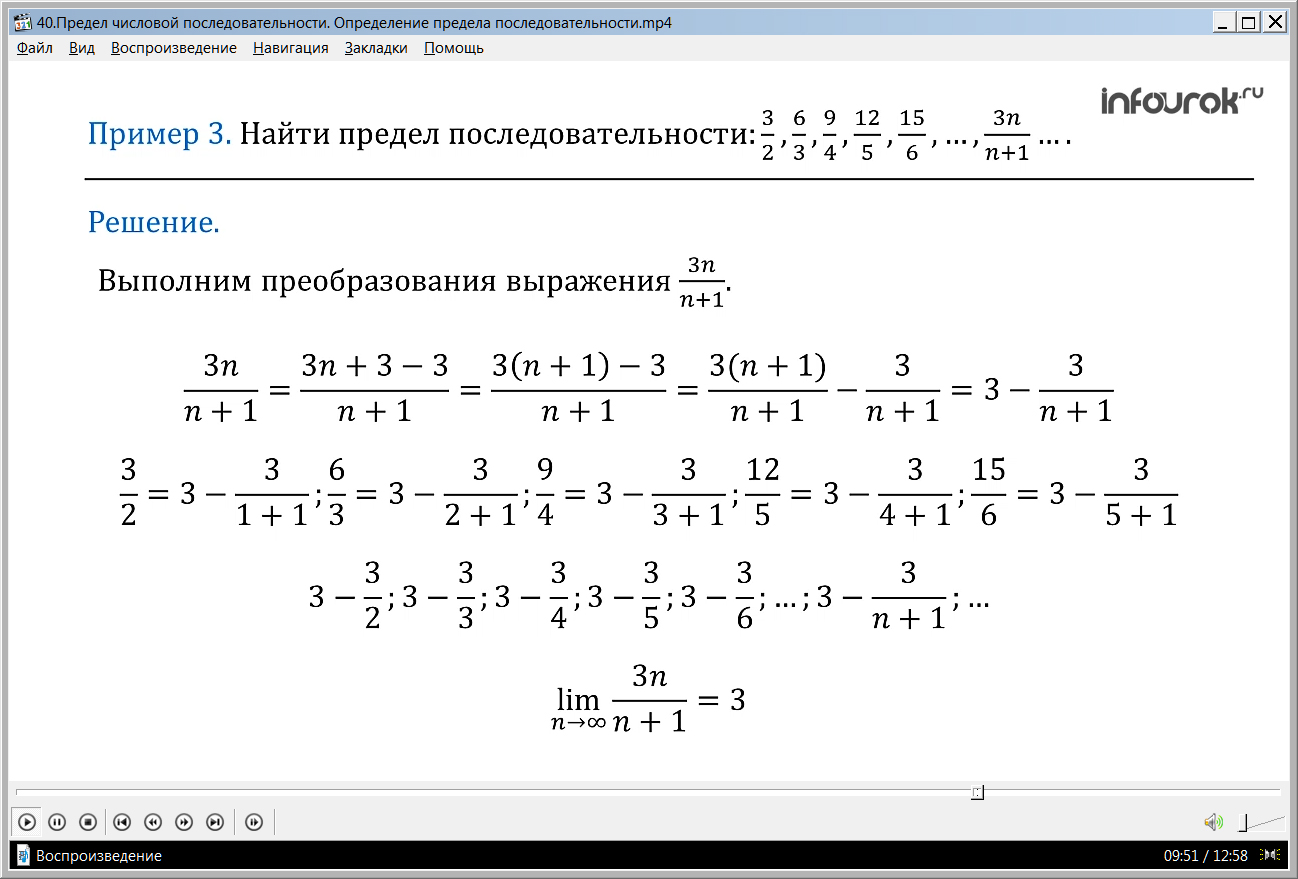
Пример 3. Найти предел последовательности:
Решение. Выполним некоторые преобразования выражения (три эн, деленное на эн плюс один).
Имеем:
( в числителе прибавим и отнимем число три, затем сгруппируем и вынесем общий множитель три за скобки;
далее каждое слагаемое разделим на знаменатель, получим разность двух дробей : первую дробь сократим на эн плюс один и получим конечный результат три минус дробь три, деленное на эн плюс один).
Это значит, в частности, что
и т.д., а потому заданную последовательность можно переписать так:
То есть видим, что «точкой сгущения» является 3; иными словами, последовательность сходится к числу 3:
(предел последовательности три эн, деленное на эн плюс один, при стремлении эн к бесконечности равен трем).
А теперь обсудим результаты, полученные в 3-х рассмотренных примерах, с геометрической точки зрения. Для этого построим графики последовательностей уn =– (игрек энный равен минус один, деленный на эн), yn=( игрек энный равен одна третья в энной степени), yn=( игрек энный равен три эн, деленное на эн плюс один), т.е. графики функции:
у =–, xN, (игрек равен минус один деленный на икс) y= ,xN(игрек равен одна третья в степени икс), y=, xN. ( игрек равен три икс, деленное на икс плюс один) (эн принадлежит множеству натуральных чисел).
График первой из этих трех функций изображен на рис. 4. Он состоит из точек с абсциссой 1, 2, 3, 4, ..., лежащих на ветви гиперболы у = – ( игрек равен минус один, деленный на икс).
Рис. 4
У второй функции аргумент х содержится в показателе степени, поэтому такую функцию называют показательной. На рис. 5 изображен график функции y=,xN. (игрек равен одна третья в степени икс). И он состоит из точек с абсциссами 1, 2, 3, ..., лежащих на некоторой кривой, — ее называют экспонентой.
Сначала сроим график функции у = ( игрек равен три икс, деленное на икс плюс один) или, что то же самое, у =, ( игрек равен сумме минус три, деленное на икс плюс один, и трех) (рис. 6)
А затем выбираем ту часть графика, которая дает представление о графике последовательности уn =. И состоит он из точек с абсциссами 1, 2, 3, 4, .. и т.д. ., лежащих на правой ветви гиперболы (рис. 7).
На всех трех рисунках точки графика, по мере их ухода вправо, все ближе и ближе подходят к некоторой горизонтальной прямой: на рис. 4 – к прямой
у = 0 (игрек равен нулю), на рис. 5 – к прямой у = 0, на рис. 7 – к прямой
у = 3. Каждую из этих прямых называют горизонтальной асимптотой графика. То есть предел последовательности является горизонтальной асимптотой функции f(n), nN (эф от эн, эн принадлежит множеству натуральных чисел).
ВЫВОД:
равенство (предел функции эф от эн равен бэ) означает, что прямая у=b(игрек равен бэ) является горизонтальной асимптотой графика функции y = f(n) (игрек равен эф от эн) (рис. 8).
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8393 |
| Номер материала | 863 |