
Урок "Предел функции"

Краткое описание документа:
Видеоурок «Предел функции» представляет учебный материал для изучения данной темы на уроке математики. В ходе изучения темы производится сравнение асимптоты функции и ее предела, правил вычисления пределов, понятие о приращении функции, описываются примеры решения задач. С помощью видеоурока есть возможность улучшить подачу материала, запоминание и понимание материала.
Видеоурок начинается с представления темы и напоминания ученикам понятия асимптоты графика функции. Отображается определение горизонтальной асимптоты y=f(n), где n – натуральные числа. Асимптота определяется пределом данной функции lim f(n)=b при n→∞ и представляет собой на координатной плоскости прямую y=b.
Аналогично роль асимптоты раскрывается для функции. Рассматривается некоторая функция y=f(x) с областью определения D(f)=[a;+∞). Известно, что y=b представляет горизонтальную асимптоту данной функции, то есть lim f(х)=b при x→+∞. Стремление функции на бесконечности к некоторому пределу – асимптоте y=b отображается на рисунке, где изображена координатная плоскость, на ней график y=f(x) и асимптота y=b. График стремится к асимптоте в положительном направлении оси абсцисс.
Далее рассматривается случай, когда график функции y=f(x) стремится к горизонтальной асимптоте при определении ее на промежутке D(f)= (-∞;a]. Замечено, в этом случае асимптота определяется пределом функции при х→-∞. На рисунке отображается приближение графика функции к асимптоте при стремлении его в сторону -∞.
Раскрываются особенности поведения функции, имеющей одинаковый предел при стремлении к +∞ и к -∞. Одновременное выполнение соотношений lim f(х)=b при x→+∞ и lim f(х)=b при x→-∞ означает, что функция в обоих направлениях стремится к асимптоте y=b. В записи подобное поведение объединяется соотношением lim f(х)=b при x→∞. Такое поведение функции отображается на сопровождающем объяснение рисунке. На нем начерчен график функции, прямая y=b и приближение графика функции к асимптоте в обоих направлениях.
Указываются свойства предела функции, стремящейся к некоторому пределу на бесконечности. Они аналогичны свойствам пределов последовательностей. Сначала представляется предел одной их популярных функций на бесконечности lim k/хm=0 при x→∞. Для двух функций с определенными пределами lim f(х)=b при x→∞ и lim g(х)=c при x→∞ являются верными следующие свойства:
- Предел функции, представляющей собой сумму двух функций f(х) и g(х), вычисляется суммой пределов каждой функции lim (f(х)+ g(х))= b+ c при x→∞.
- Предел произведения функций равен произведению пределов каждой из них lim (f(х)·g(х))=bc при x→∞.
- Для нахождения предела частного двух функций необходимо найти частное пределов каждой функции lim (f(х)/g(х))=b/c при x→∞. При этом должно быть g(х)≠0 и с≠0.
- Для функции, в которой можно выделить постоянный множитель, верно lim kf(x)=kb при x→∞.
Для усвоения темы рассматривается решение примеров с применением полученных знаний. Необходимо вычислить lim (√3)х5-17/(х5+9) при x→∞. Для вычисления предела числитель и знаменатель функции делятся на высшую степень аргумента. В результате вычисления получается lim (√3)х5-17/(х5+9)=lim (√3-17/ n5)/(1+9/n5) при x→∞. После применения свойства предела частного, вычисленное значение предела lim (√3)х5-17/(х5+9)=√3 при x→∞.
Отдельно на экран выводится замечание о том, что решение предела функций аналогично решению предела последовательностей. Разница в решении определяется наличием аргумента х, для которого недопустимо обращение знаменателя в нуль. Поэтому, как указано в замечании, в последнем примере не может быть х=-5√9, так как в этом случае знаменатель равен нулю.
Также рассматривается понятие предела функции lim f(x)=b при x→а. Указана возможность трех основных ситуаций при приближении к точке. На рисунке изображены три координатные плоскости, на каждой их которых – график функции y=f(x). На первых двух рисунках отмечен разрыв функции в (a,b). При этом на первом графике функция не имеет значения в точке, на втором – принимает иное значение, не принадлежащее линии графика, а в третьем случае – разрыв отсутствует. Все три функции имеют одинаковые графики, отличающиеся поведением в х=а. И при этом во всех lim f(x)=b при х→а.
На основании рассмотренных примеров вводится понятие непрерывной в точке функции. Она определяется как функция, удовлетворяющая условию lim f(x)= f(а) при x→а. Также вводится понятие функции, что непрерывна на промежутке Х, если она в каждой точке промежутка будет непрерывной. Для усвоения материала рассматривается непрерывность основных изученных функций. Подчеркивается непрерывность на числовой прямой функций постоянной, линейной, квадратичной, степенной и модуля. Непрерывной на луче [0;+∞) является функция у=√х. Функция у=х-n непрерывна на промежутках (0;+∞) и (-∞; 0) с разрывом в точке х=0. Отмечается непрерывность на числовой прямой тригонометрических функций y=sin x и y=cos x, а функций y=tg x и у=ctg x – на промежутках, входящих в область определения. Обобщая рассмотренные случаи, на экране отображается вывод о непрерывности в любой точке области определения функций, состоящих из выражений, включающих иррациональные, рациональные, тригонометрические выражения.
Далее предлагается для усвоения темы рассмотреть решение нескольких примеров. В примере 2 необходимо вычислить предел функции lim(x3+3x2-11x-8) при х→-1. Используя непрерывность функции и свойство предела суммы функций, находим значение предела lim(x3+3x2-11x-8)=5 при х→-1. В примере 3 описывается нахождение lim(cos πx/√x+6) при х→1. Зная, что функция определена, а также непрерывна в любой ее точке, в том числе и точке х=1, то в ней она принимает значение в ней f(1), то есть lim(cos πx/√x+6)=-1/7 при х→1. В примере 4 рассматривается решение предела, где необходимо преобразовать выражение под знаком предела. Необходимо вычислить lim((x2-25)/(x-5)) при х→5. Подставив сразу х=5 в выражение, частное не имеет смысла, поэтому дробь сокращается. Полученное после сокращения выражение х+5 является тождественным исходному, если х≠5. Предел выражения при х→5 равен 10.
В замечании к изученным свойствам основных функций рассматривается поведение функции (sin t)/t при t →0. Отмечается, что сама функция и, так как она непрерывна, ее предел тоже стремятся к 1, то есть lim(sin t/t)=1 при t →0.
Рассматриваются понятия приращения функции и аргумента. Дается определение приращения аргумента, выраженного разностью х1-х0, приращения функции f(x1)-f(x0) для функции у= f(x), что непрерывна в рассматриваемых точках. Вводятся обозначения приращения аргумента Δх=х1-х0 и Δу =f(x1)-f(x0). Отмечается, что иначе Δу =f(х0+Δх)-f(x0). Для усвоения понятий приращения функции и аргумента рассматривается решение примеров на их нахождение.
Описывается связь предела и приращения функции, связывая различные представления непрерывности функции и отмечая, что в этой точке приращение Δу→0. Отдельно выделяется условие непрерывности – если Δх→0, то Δу→0.
Для закрепления полученных знаний рассматривается нахождение приращения линейной функции y=kx+m при изменении аргумента х+Δх. Он равен Δу=kΔх. Предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю lim Δу/Δх= lim kΔх/ Δх=k. Анализ также делается с помощью рисунка, где изображен график функции и описывается ее поведение.
В примере 7 рассматривается решение задания, где для функции у=х3 определяется приращение функции при х+Δх, предел отношения приращения Δу/Δх.
Видеоурок «Предел функции» может применяться на традиционном уроке математики для повышения его эффективности. Также материал может быть полезен для обеспечения наглядности в ходе дистанционного обучения. Ученикам, которым требуется дополнительное объяснение темы, можно рекомендовать видеопособие для самостоятельного рассмотрения.
ТЕКСТОВАЯ РАСШИФРОВКА:
При изучении предела числовой последовательности мы рассматривали функцию y= f (n)(игрек равный эф от эн), гдеnN(эн принадлежит множеству натуральных чисел) и получили результат, что равенство ( предел эф от эн равен бэ) означает, что прямая у = b(игрек равный бэ) является горизонтальной асимптотой графика функции у =f (n) (игрек равный эф от эн).
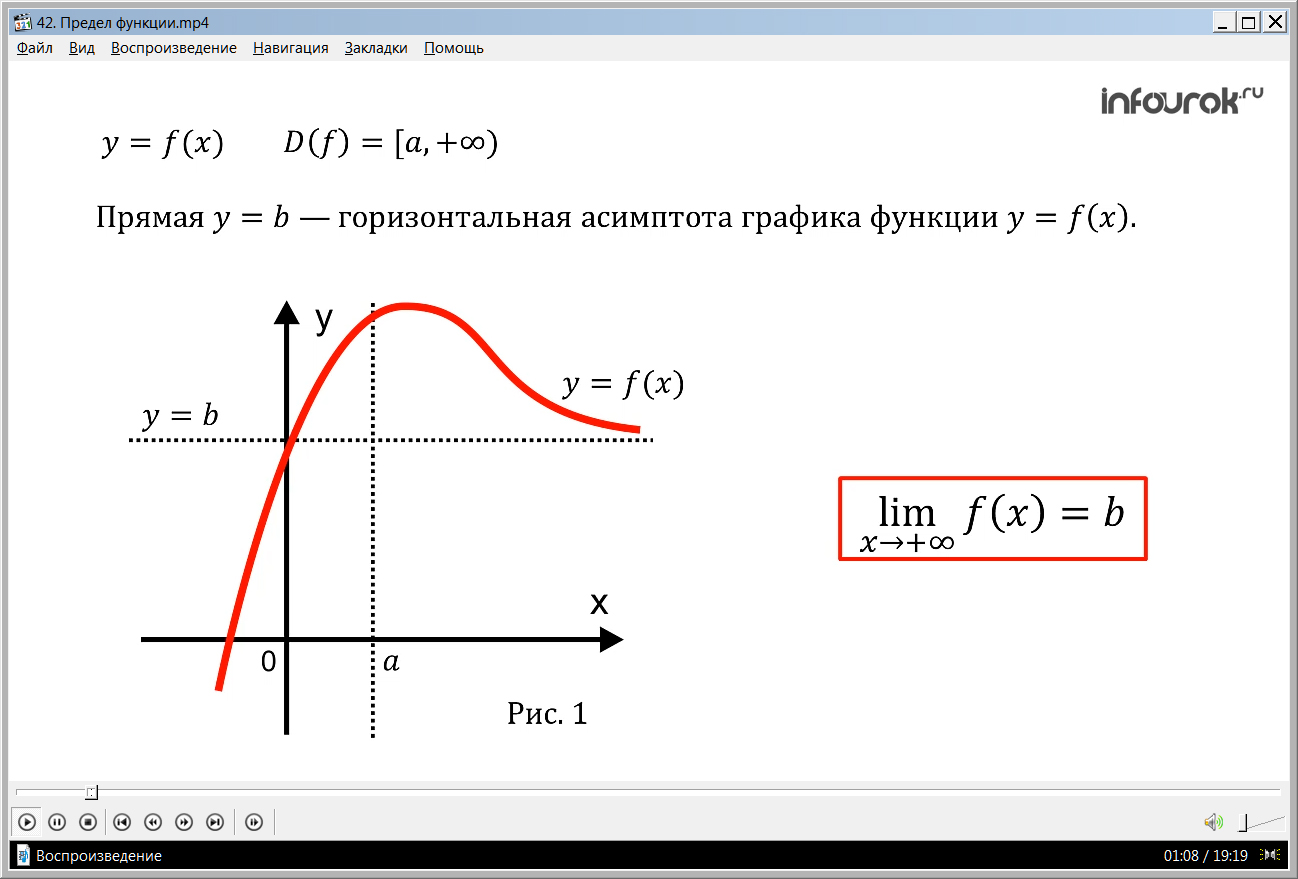
Пусть теперь дана функция у =f (x)( игрек равный эф от икс), в области определения которой содержится луч [а, +), (от а до плюс бесконечности) и пусть прямая у = b(игрек равный бэ) является горизонтальной
асимптотой графика (рис. 1) функции у =f(x). (игрек равный эф от икс). То воспользуемся равенством: (читают: предел функции у = f(x) (игрек равный эф от икс) при стремлении х (икс) к плюс бесконечности равен b).
Рис. 1
Если же дана функция у = f (x) (игрек равный эф от икс), в области определения которой содержится луч (–, а](от минус бесконечности до а), и прямая у = b(игрек равен бэ)является горизонтальной асимптотой графика функции у = f(x) (игрек равный эф от икс) (рис. 2), то в этом случае используют запись: (читают: предел функции у = f(x) (игрек равный эф от икс) при стремлении х к минус бесконечности равен b).
Рис 2
(предел функции у = f(x) (игрек равный эф от икс) при стремлении х (икс) к плюс бесконечности равен b) и (предел функции
у = f(x) (игрек равный эф от икс) при стремлении х к минус бесконечности равен b), то можно объединить их одним соотношением: . Но условились использовать следующую запись:
(читают: предел функции у =f(х) при стремлении х к бесконечности равен b).
Рис. 3
В этом случае прямая у = b является горизонтальной асимптотой графика функции у = f(x) как бы с двух сторон (рис. 3).
Предел функции на бесконечности вычисляется по тем же правилам, что и вычисление предела последовательности. Сформулируем их.
Правила вычисления предела функции на бесконечности:
1) Для любого натурального показателя т и любого коэффициента k справедливо соотношение:
2)Если , , mo
а) предел суммы равен сумме пределов:
б) предел произведения равен произведению пределов:
в) Предел частного равен частному от деления пределов (при условии, что g(x)0 и с 0):
г) постоянный множитель можно вынести за знак предела:
Пример 1. Вычислить . (предел дроби корень из трех икс в пятой минус 17, деленное на икс в пятой плюс 9).
ЗНАК σ НУЖНО ЗАМЕНИТЬ НА х.
Решение. Разделим числитель и знаменатель дроби почленно на х5:
Осталось воспользоваться правилом «предел частного». Поскольку
предел числителя равен – 0=(корень из трех), а предел знаменателя равен 1–0 = 1 (единица), то предел дроби равен .(корень из трех)
Ответ: =.
Замечание. Решаются пределы функций точно также как и пределы числовых последовательностей, отличие только в том, что переменная х может быть любым действительным числом, кроме значения (минус корень пятой степени из девяти), которое обращает в нуль знаменатель дроби, содержащейся под знаком предела.
2. Предел функции в точке
Рассмотрим функции, графики которых изображены на рис. 4(а-в). Во всех трех случаях изображена одна и та же кривая, тем не менее это три разные функции, они отличаются друг от друга своим поведением в точке х =а (икс равен а). Для функции у = f(x), график которой изображен на рис. 4(а), значение f(a) (эф от а) не существует, потому что функция в указанной точке не определена. Для функции у = f(x), график которой изображен на рис. 4(б), значение f(a) существует, но оно находится не на кривой графика, то есть отлично от b (бэ). Наконец, для функции у = f(x), график которой изображен на рис. 4(в), значение f(a) существует, и лежит на кривой то есть равно b. Если же точку х =а исключить из рассмотрения, то все три функции будут тождественными.
Для всех трех случаев используется одна и та же запись:
(читаем: «предел функции у =f(x) при стремлении х к а равен b»).
Введем определение непрерывной функции.
Непрерывной считают функцию у =f(x), которая удовлетворяет условию
( предел функции у =f(x) при стремлении х к а равен эф от а), в нашем примере функция изображенная на третьем графике.
Иными словами, функцию у = f(х) называют непрерывной в точке х=а, если предел функции y = f(x) при стремлении х к а равен значению функции в точке х=а.
Функция y = f(x) называют непрерывной в точке х = а, если выполняется соотношение: . (только на экран как определение)
А также функцию y= f(x) называют непрерывной на промежутке X(икс большое), то есть на ее области определения, если она непрерывна в каждой точке промежутка.
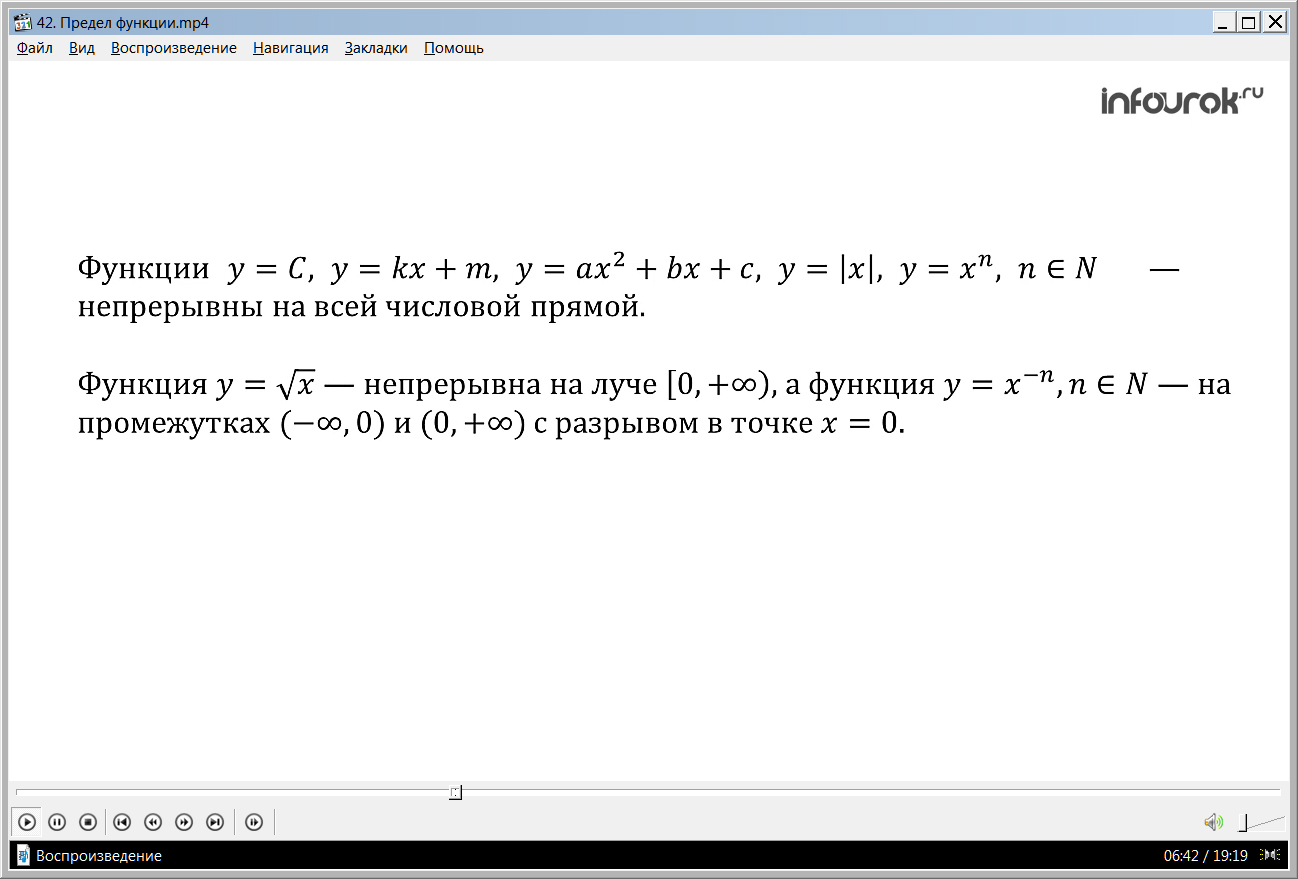
Рассматривая функции y=C, y = kx + m, y=ax2 + bx+c, y=|x|, y=xn, где n — натуральное число, мы знаем что они — непрерывны на всей числовой прямой.
Функция у = (игрек равен корень квадратный из икс) непрерывна на луче [0, +), а функция у = х–n(игрек равен икс в минус энной степени)
(n — натуральное число) непрерывна на промежутках (–, 0) и (0, +), но претерпевает разрыв в точке х = 0.
Тригонометрические функции у = sinx и у=cosx непрерывны на всей числовой прямой, а функции у= tg х, y=ctgx непрерывны в каждом промежутке из области их определения.
Таки образом, из всего вышесказанного сделаем вывод:
Если выражение f(x) составлено из рациональных, иррациональных, тригонометрических выражений, то функция y=f(x) непрерывна в любой точке, в которой определено выражение f(x).
Рассмотрим несколько примеров на вычисление пределов функций.
Пример 2. Вычислить: . (предел выражения икс в кубе плюс три, умноженное на икс во второй, минус 11 икс минус 8 при икс стремящемся к минус одному).
ЗНАК σ НУЖНО ЗАМЕНИТЬ НА х.
Решение. Выражение х3 +3х2 – 11х –8 определено в любой точке х, в частности, в точке х = –1. Следовательно, функция у = х3 +3х2 – 11х –8 непрерывна в точке х = –1, а потому предел функции при стремлении х к –1 равен значению функции в точке х = –1.
Имеем: . (получили, что предел равен пяти)
Ответ: 5.
Пример 3. Вычислить: (предел косинус пи икс, деленное на корень из икс плюс шесть при стремлении икс к одному).
Решение. Выражение f(x) = определено в любой точке х ≥ 0, в частности, в точке х = 1. Следовательно, функция у = f(х) непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению
функции в точке х =1. Имеем: === ( получили предел равен минус одной седьмой)
В рассмотренных примерах вычисление пределов сводилось к нахождению значение функции в точке, к которой стремится аргумент х.
Но часто что бы найти предел функции необходимо выражение, стоящее под знаком предела, сначала преобразовать. Рассмотрим пример.
Пример 4. Вычислить (предел икс в квадрате минус двадцать пять, деленное на икс минус пять)ЗНАК σ НУЖНО ЗАМЕНИТЬ НА х.
Решение. Если подставить значение х = 5 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на 0 делить нельзя. Но заданную алгебраическую дробь можно сократить:
Значит, функции у = и у = х+5 тождественны при условии х5.
Но при вычислении предела функции при х 5 (икс стремится к пяти) саму точку х = 5 можно исключить из рассмотрения, мы об этом говорили выше. Значит,
5+5=10 (предел икс в квадрате минус двадцать пять, деленное на икс минус пять равно десять).
Ответ: 10.
Замечание.
Рис 5

Возьмем числовую окружность, выберем достаточно малое положительное значение t, отметим на окружности точку M(t) и ее ординату, т.е. sint; t– это длина дуги AM, sint — это длина перпендикуляра МР . Для достаточно малых значений t выполняется приближенное равенство
AMМР, т.е. sintt, и, следовательно, . Например, ; ; . То есть, получаем равенство, которое называют первый замечательный предел:
(предел отношения синуса тэ к тэ при стремлении тэ к нулю равен единице ).
3. Приращение аргумента. Приращение функции .
Для того, чтобы изучить поведение функции у = f(x) (игрек равен эф от икс) около конкретной точки х0,(икс нулевой) важно знать, как меняется значение функции при изменении значения аргумента. Для этого используются понятия приращений аргумента и функции.
Определение 1. Пусть функция у =f(x) определена в точках х0 и х1. Разность х1 –х0 называют приращением аргумента (при переходе от точки х0 к х1), а разность f(x1) –f(x0) (эф от икс первого минус эф от икс нулевого) называют приращением функции.
Приращение аргумента обозначают х (читают: «дельта икс»; — прописная буква греческого алфавита «дельта»). Приращение функции обозначают у (дельта игрек) или f (дельта эф).
Итак, х1–х0 =х, значит, х1 =х0 +х (икс первый минус икс нулевой равно дельта икс, значит, икс первый равен икс нулевой плюс дельта икс)
f(x1)–f(x0) = y(или f), значит,
y=f(x0+x)–f(x0). (Дельта игрек равен эф от икс нулевого плюс дельта икс минус эф от икс нулевого)
Пример 5. Найти приращение функции у = х2 при переходе от точки
х0 = 2 к точкам: а) х = 2,1; б) х = 1,98.
Решение,
а)f(2)=22=4; f(2,1)=2,12 =4,41;
y= f(2,1)– f(2)=4,41–4=0,41
б)f(2)=4; f(1,98) = 1,982 =3,9204;
y= f(1,98)– f(2)=3,9204–4= –0,0796.
Обратите внимание на полученный ответ: приращение функции (как, впрочем, и приращение аргумента) может быть и положительным, и отрицательным числом, так что не стоит понимать термин «приращение» как «прирост».
А теперь посмотрим на определение непрерывной функции с точки зрения приращений аргумента и функции. Определение непрерывности функции в точке х =а выглядит так: . Здесь ха, значит, (х–а) 0, т.е. x0. При этом f(x) f(a), значит,(f(x)–f(a)) 0, т.е. y0.
Получаем новое истолкование понятия непрерывности функции в точке.
Функция у = f(x) непрерывна в точке х =а, если в точке х=а выполняется следующее условие:
если x0, то y0. (дельта икс стремится к нулю, то дельта игрек стремится к нулю).
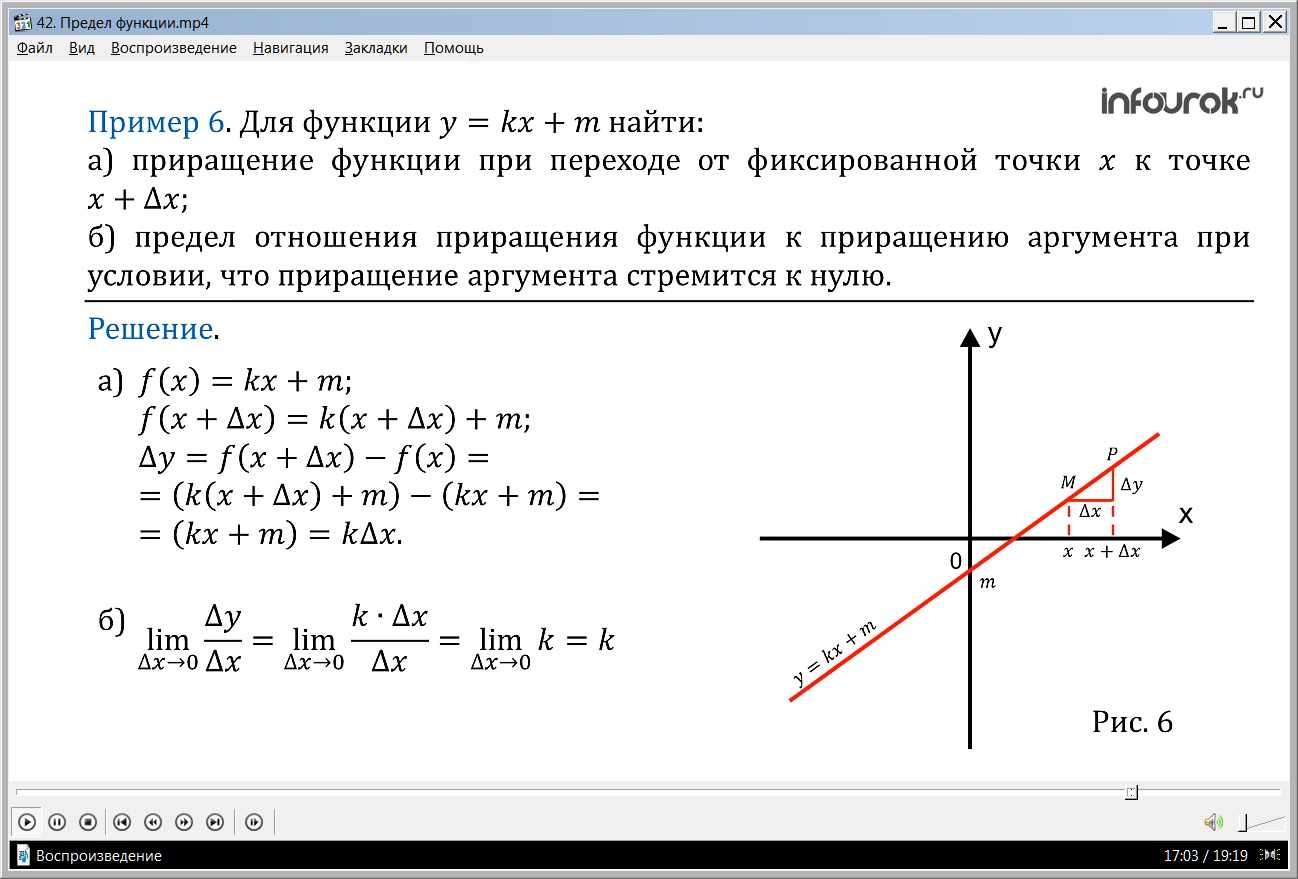
Пример 6. Для функции y = kx + m найти:
а) приращение функции при переходе от фиксированной точки х к точке
х + x;
б) предел отношения приращения функции к приращению аргумента
при условии, что приращение аргумента стремится к нулю.
Решение. а) Имеем:
f(x)=kx + m;
f(x + x)=k(x + x) +m;
y=f(x+x)–f(x)=(k(x+x)+m) –(kx+m)= (kx+kx+m)–(kx+m)=k·x.
Итак, для данной линейной функции y=kx + m получили приращение: y=k·x.
б) Нужно вычислить. (предел дельта игрек к дельта икс при дельта икс стремящемся к нулю). Имеем:
===k
Итак, для заданной линейной функции y=kx + m получили: =k.
Рис 6
На рис. 6 изображен график линейной функции у = kx+m, и показана точка графика М(х, f(x)), (эм с координатами икс и эф от икс ), а также отмечены приращение аргумента и приращение функции при переходе от точки х к точке х+х. По чертежу видно, что ( дельта игрек, деленное на дельта икс) — есть тангенс угла между прямой у = kx + m и положительным направлением оси х, а это — есть угловой коэффициент прямой. Следовательно,
= k, что и получено при решении примера 6.
Пример 7. Для функции у = х3 найти:
а) приращение функции при переходе от фиксированной точки х к точке
х + х;
б) предел отношения приращения функции к приращению аргумента
при условии, что приращение аргумента стремится к нулю.
Решение. а) Имеем:
f(x)=x3;
f(x+x)=(x+x)3;
у = f(x+x)–f(x)= (x+x)3– x3= (x3+3x2x+3х(Δх)2+(x)3)– x3= 3x2x+3х(Δх)2+(x)3=(3x2+3хΔх+(x)2)Δх
Итак, для функции у = х3 получили: у = (3x2+3хΔх+(x)2)Δх.
б) Нужно вычислить
Имеем: ===3x2
При вычислении последнего предела мы учли, что х – фиксированная
точка, т.е. постоянное число, а х — переменная: если х0, то
(3x2+3хΔх+(x)2)3x2.
Итак, для заданной функции у = х3 получили: = 3х2.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13173 |
| Номер материала | 865 |