
Урок "Преобразование произведений тригонометрических функций в суммы"

Краткое описание документа:
Данный видеоурок составлен для учеников 10 класса. С помощью нее они смогут изучить тему «Преобразования произведений тригонометрических выражений в суммы». Сопровождается обучающий материал спокойным мужским голосом. С помощью нее можно провести интересный и познавательный урок в школе. Благодаря иллюстрациям и определениям, которые выводятся понятным текстом на экран, школьники смогут быстрее и эффективнее понять данную тему.
Несмотря на то, что тригонометрия, как наука, появилась достаточно давно, она не утратила свою актуальность и по сей день. В различных науках появляются задачи, при решениях которых школьникам придется столкнуться с данной областью. По этой причине, они должны уметь справляться с примерами различной сложности, рассматривать функции, содержащие синусы, косинусы, тангенсы и котангенсы и т.д.
Так как тригонометрия содержит в себе огромное количество формул, без которых упрощения того или иного выражения заняло бы огромное количество времени. Поэтому очень важным является запоминание и понимание этих формул. Если понять способ их выведения, можно с легкостью их запомнить и применять на практике. Для того чтобы они остались в памяти на долгое время, необходимо укрепить их на практике. Поэтому, необходимо учителям задавать на дом большое количество тригонометрических выражений и уравнений школьникам.

Данный видеоурок составлен профессионалами. Он имеет последовательную структуру, нет никакой лишней и ненужной информации, которая отклоняется от учебного плана.
Школьникам уже известно, как необходимо преобразовывать тригонометрические уравнения суммы в произведение. Как же выполняться при необходимости обратный процесс? Иногда для упрощения того или иного выражения это будет являться необходимостью.
Начинается рассмотрения с приведения примера. Записывается произведения синуса некоторого tна косинус такого же значения. Преобразовывается данное выражение через дробь, где в числителе мы видим сумму синуса суммы аргументов и разности, деленную на 2.
Аналогичным образом преобразовывается произведение синус некоторого s на синус t.
Для того чтобы закрепить данные выражения практикой предлагается решить некоторые примеры. В первом из них предлагается найти числовой ответ для выражения, представляющее собой произведение синуса 2х на косинус 9х. При решении данного примера используется ранее изученная формула. На экране выводится подробное решение примера, также показывается, какая именно формула используется.
Далее рассматривается еще один пример, где предлагается преобразовать произведение в сумму. С правой стороны выводятся все выкладки и объяснения. Понять, как решается этот пример не так сложно, ведь диктор все подробно комментирует.
Третий пример предлагает упросить выражение, которое состоит из произведения трех синусов некоторых градусных величин. При упрощении используется формула преобразования произведения синусов в сумму. При решении данного примера обращается внимание на то, что функция косинуса является четной функцией. Таким образом, правильно определяются знаки. Выводится ответ. Решение достаточно объемное, однако, если пошагово его рассмотреть, то ничего непонятного не останется.
Четвертый же пример содержит тригонометрическое уравнение, при решении которого необходимо использовать изученные формулы, как на данном уроке, так и на предыдущих видео.
Как уже было сказано, с помощью данной презентации можно провести интересный урок для десятиклассников. Скачать материал могут и репетиторы и школьники. С помощью него, можно визуально показать ученику пошаговое решение примеров, на подобии которых будут попадаться школьникам, как во время выполнения домашних заданий, так и на самостоятельных и контрольных работах в школе.
ТЕКСТОВАЯ РАСШИФРОВКА:
Преобразование произведений тригонометрических выражений в суммы
Вам уже известно, что любая математическая формула на практике применяется справа налево и слева направо. Следовательно, применяя формулу в обратном направлении, мы можем произведение тригонометрической функции преобразовать в сумму.
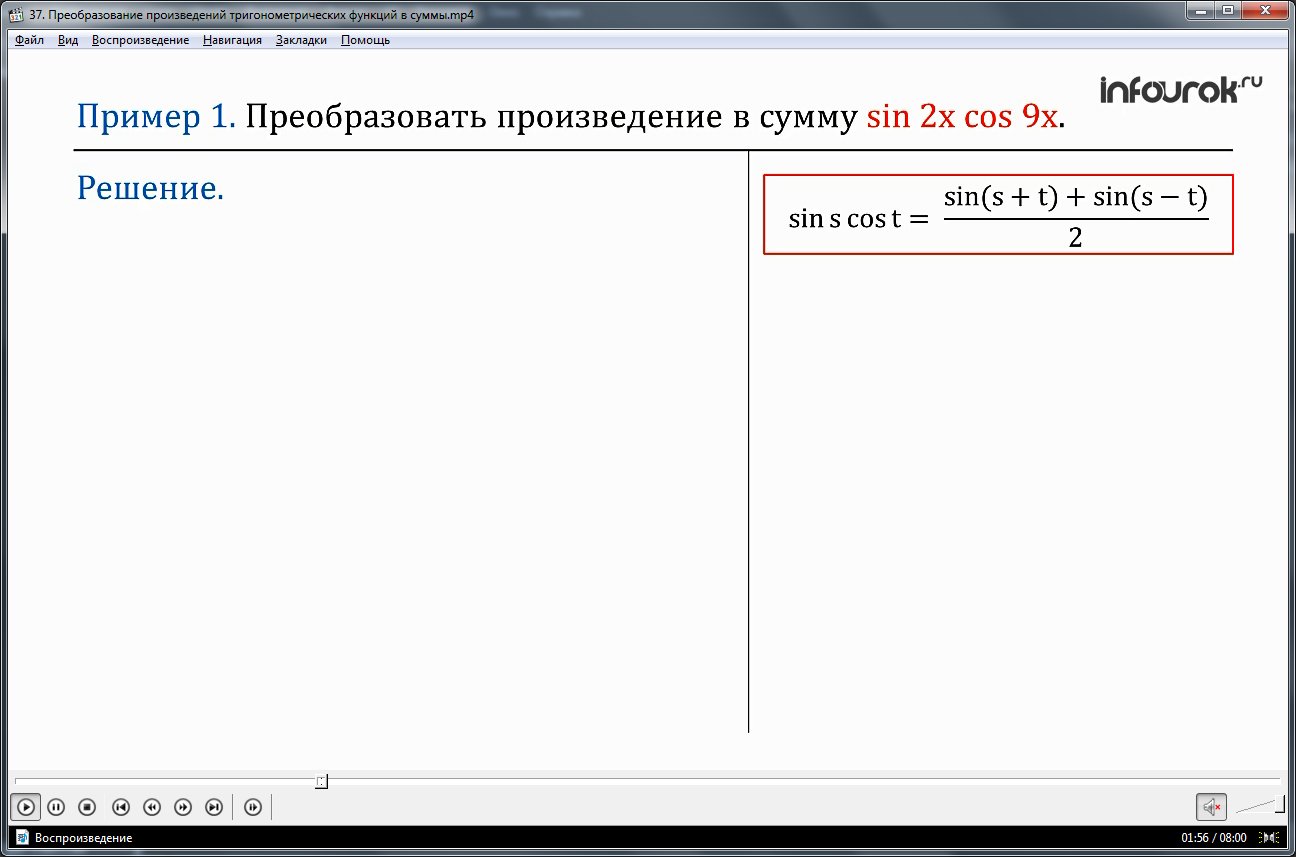
Рассмотрим пример:
из формулы преобразования сумм синусов аргументов ес и тэ в произведениеsin(s +t) + sin(s - t) = 2 sinscost
можно получить еще одну формулу:
sinscost = (произведение синуса аргумента эс на косинус аргумента тэ равно полусумме синуса суммы аргументов эс и тэ и синуса разности аргументов эс и тэ, причем разность берется так, что из аргумента, стоящего под знаком синуса, вычитается угол, стоящий под знаком косинуса.)
sin(s + t) + sin(s - t) = 2 sin s cos t
sinscost =
Аналогично, из формулы преобразования сумм косинусов аргументов ес и тэ в произведение cos (s+t)+ cos(s - t) =2 cosscost получим
cosscost = (произведение косинусов аргументов эс и тэ равно полусумме косинуса суммы этих аргументов и косинуса их разности).
И из формулы преобразования разности косинусов аргументов ес и тэ в произведениеcos (s+t) - cos(s - t) = - 2sinssint имеем
sinssint= (произведение синусов аргументов эс и тэ равно полуразности косинуса разности этих аргументов и косинуса их суммы).
Рассмотрим примеры.
ПРИМЕР 1. Преобразовать произведение в сумму sin2х cos9х.
Решение. При решении будем использовать формулу sinscost = , где s= 2х, t=9х. Тогда запишем
sin2хcos 9х = = (учитывая, что
sin (-у) = - sin у, получим) = ( полуразность синуса одиннадцати икс и синуса семи икс).
Ответ: sin2х cos9х=.
ПРИМЕР 2. Преобразовать произведение в сумму cos(2х – у) cos(х + 4у) (произведение косинуса аргумента два икс минус игрек на косинус аргумента икс плюс четыре игрек).
Решение. При решении будем использовать формулу cosscost = , где s= (2х-у), t=(х+4у). Тогда
cos(2х – у) cos(х + 4у) = = раскроем скобки = , произведем вычисления и получим
= (полусумма косинуса аргумента три икс плюс три игрек и косинуса аргумента икс минус пять игрек).
Ответ: .
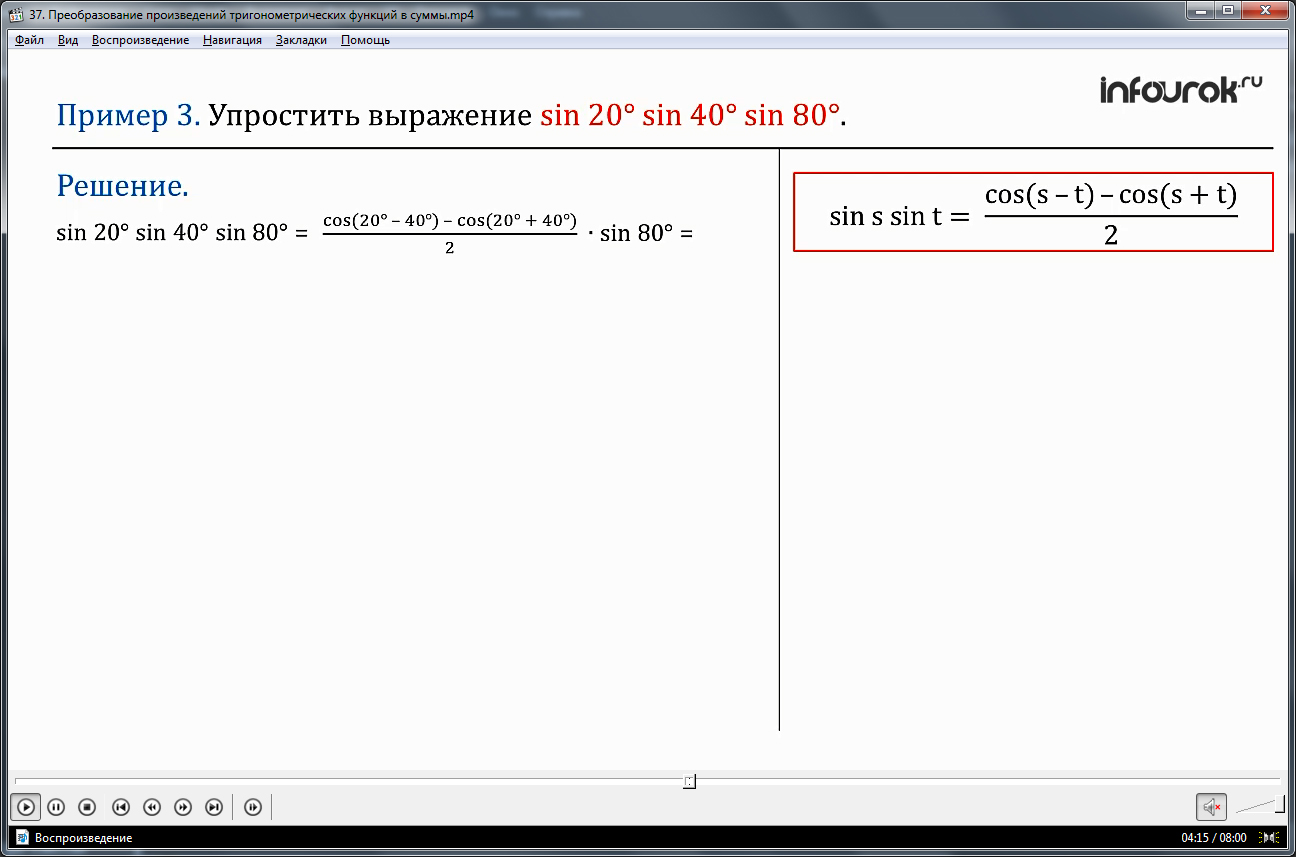
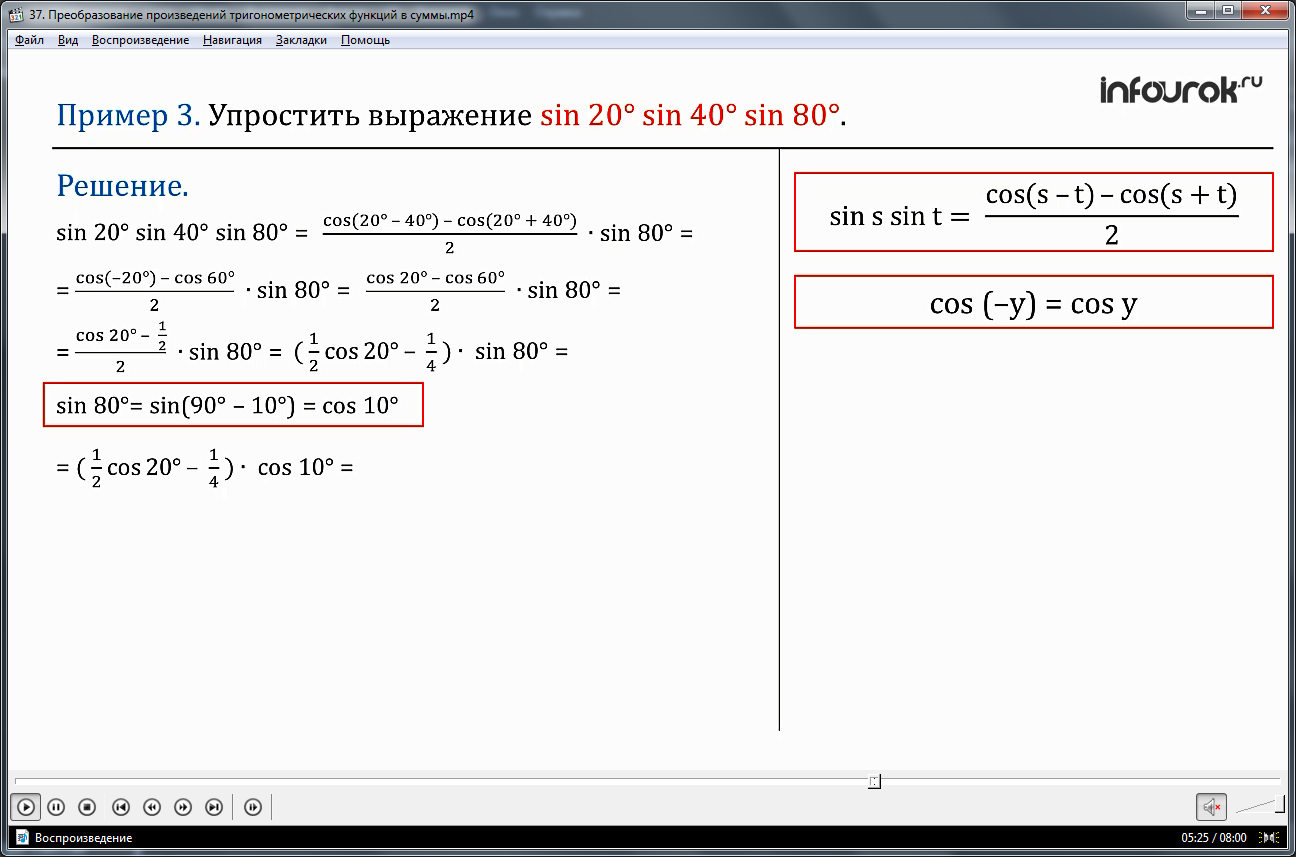
ПРИМЕР 3. Упростить выражение sin20°sin40° sin80°.
Решение. Применим формулу: sinssint= .
Имеем
sin 20°sin 40° sin 80°= ∙ sin 80°= ∙ sin 80°=
( учтем, что косинус – функция четная, значит,
= ∙ sin 80° Так как cos60°=
= ∙ sin 80°= ∙ ) ∙ sin 80°=
( заметим, что sin 80°= sin(90° - 10°)= cos10°, значит получим, что)
= ∙ ) ∙ cos10° = раскроем скобки = ∙ cos10° - ∙ cos10°
( применим формулу cosscost = )
= ∙ - ∙ cos10°= ∙() - ∙ cos10°=
раскроем скобки
(вспомним, что = )
Ответ: sin20°sin40° sin80° = .
ПРИМЕР 4. Решить уравнение 2 sin2х cos9х - sin11х =0.
Решение.
Преобразуем левую часть уравнения, используя формулу
sin s cos t = , гдеs=2x, a t=9x получим:
2 ∙ - sin11х = sin11х = .
Итак, данное уравнение равносильно уравнению = 0(минус синус семи икс равно нулю). Значит, = πn, откуда х = , .
Ответ: х = , .
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5651 |
| Номер материала | 860 |