
Урок "Преобразование сумм тригонометрических функций в произведения"

Краткое описание документа:
В десятом классе школьники будут проходить такой раздел в алгебре, как тригонометрия. Она будет изучаться на протяжении большого количества уроков.
Сама по себе тригонометрия, как наука, появилась более двух тысячелетий назад. Так как обычных алгебраических операций было бы недостаточно, чтобы выразить тригонометрические функции, ученым пришлось ввести новые обозначения. Данная наука изучает соотношения между сторонами треугольника и его углами. Во многих геометрических, алгебраических задачах появляется необходимость сталкиваться с данной областью. Задачи по физике также приводят иногда к тригонометрическим функциям.
Школьники уже изучили основные тригонометрические функции, научились строить их графики, преобразовывать, основные формулы в тригонометрии, пользоваться таблицей значений часто встречаемых в тригонометрии аргументов и т.д. К изучению данного видеоурока они уже справлялись с большим количеством тригонометрических выражений и уравнений.
В некоторых примерах появляется необходимость преобразовать формулу суммы тригонометрической функции в произведение. С помощью этого действия можно сократить и упростить огромные выражения, решить уравнения, системы уравнений и т.д.
Видеозапись «Преобразование сумм тригонометрических функций в произведения» является отличным сопровождающим материалом при изучении данной темы. Учителя могут воспользоваться примерами, которые заданы в ресурсе, определениями и формулами. Мультимедийный файл имеет отличное качество. Его можно воспроизвести во время урока. Это поможет школьникам сконцентрироваться на изучаемый предмет.
Вначале видеоурока диктор говорит о том, что на экране будут выведены некоторые формулы суммы, которые помогут при решении тригонометрических уравнений.
В первую очередь рассматривается сумма синусов. Первое выражение представляет собой сумму синуса суммы двух аргументов и синуса разности этих же аргументов. Каждый член расписывается по формулам, изученным ранее. Они выводятся в правой части экрана для того, чтобы напомнить школьникам.
При полной записи, раскрытии скобок и упрощения мы получаем произведение. Производится замена переменными. Х-ом обозначают сумму аргументов, у-ом – разность. Подставляя в полученное выражение, мы получаем первую формулу преобразования сумм в произведение в тригонометрии.
Чтобы школьники запомнили формулу, недостаточно показать способ ее получения. Необходимо попробовать решить на примере. Приводится сумма синусов некоторых значений. Преобразовывается по формуле в произведение.
Вторая формула, получение которой будет показано пошагово – это разность синусов. Чтобы не проделать дополнительно предыдущие шаги, можно воспользоваться уже полученной формулой для суммы. Необходимо вспомнить, что синус является нечетной функцией. Если записать разность в виде суммы и подставить минус в формулу от суммы, то получим новое правило преобразования разности в произведение.
Аналогичным образом приводится пример. Диктор подробно рассказывает его решение.
Сумма и разность косинусов с примерами приводятся в таком же порядке. Аналогичным образом используются ранее изученные формулы, приводится замена и выводится результат. При выведении формулы разности можно прибегнуть к тому, что косинус является четной функцией.
Далее приводится пример, в котором необходимо решить тригонометрическое уравнение. В правой части можно увидеть ноль, а в левой – сумму косинусов от некоторых значений.
При решении уравнения левая часть преобразовывается в произведение. Как известно, оно будет равняться нулю, когда некоторое из множителей будет также равняться нулю. Поэтому преобразование в произведение будет очень полезным.
Напоследок приводится еще один пример, более сложный. Можно подсказать школьникам правильно направление, и они справятся с примером самостоятельно, если поняли принцип в целом.
Видеозапись будет очень полезной для школьников, которые обучаются дома. С помощью него можно освоить важные формулы, без которых решение тригонометрических уравнений будет сложным и иногда невозможным.
ТЕКСТОВАЯ РАСШИФРОВКА:
Преобразование сумм тригонометрических функций в произведения
Сегодня мы рассмотрим еще несколько тригонометрических формул, которые позволяют сумму (разность) синусов или косинусов разложить на множители. Эти формулы вам пригодятся при решении тригонометрических уравнений.
Первая формула - СУММА СИНУСОВ.
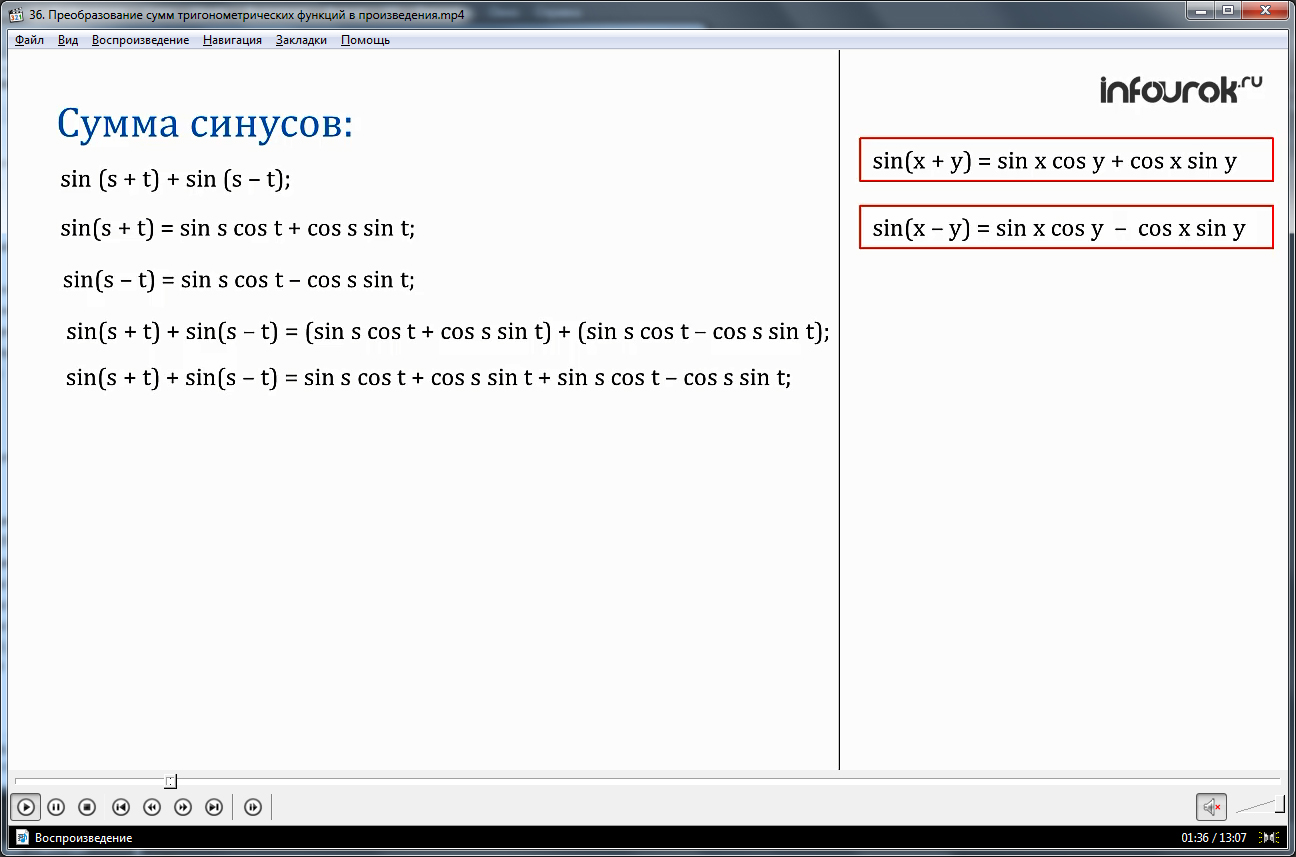
Рассмотрим выражение sin(s + t) + sin(s - t) , где sи t аргументы тригонометрических сункций.
Применим уже известные формулы синус суммы и синус разности:
sin(x + y) = sin x cos y + cos x sin y
sin(x - y) = sin xcos y - cos xsin y,
тогдавыражениеsin(s + t) будетиметьвидsin s cos t + coss sin t
а выражение sin(s - t) будет иметь вид sinscost- cosssint,
тогда получим:
sin(s + t) + sin(s - t) = (sin s cos t + coss sin t) + (sin s cos t - coss sin t)
Раскрываемскобки:
sin s cos t + coss sin t+ sin s cos t - coss sin t
проводим вычисления:
cosssint- cosssint=0
sin s cos t + sin s cos t = 2 sin s cos t.
sin(s + t) + sin(s - t) = (sin s cos t + coss sin t) + (sin s cos t - coss sin t)=sin s cos t + coss sin t + sin scos t - cos ssin t =2 sin s cos t.
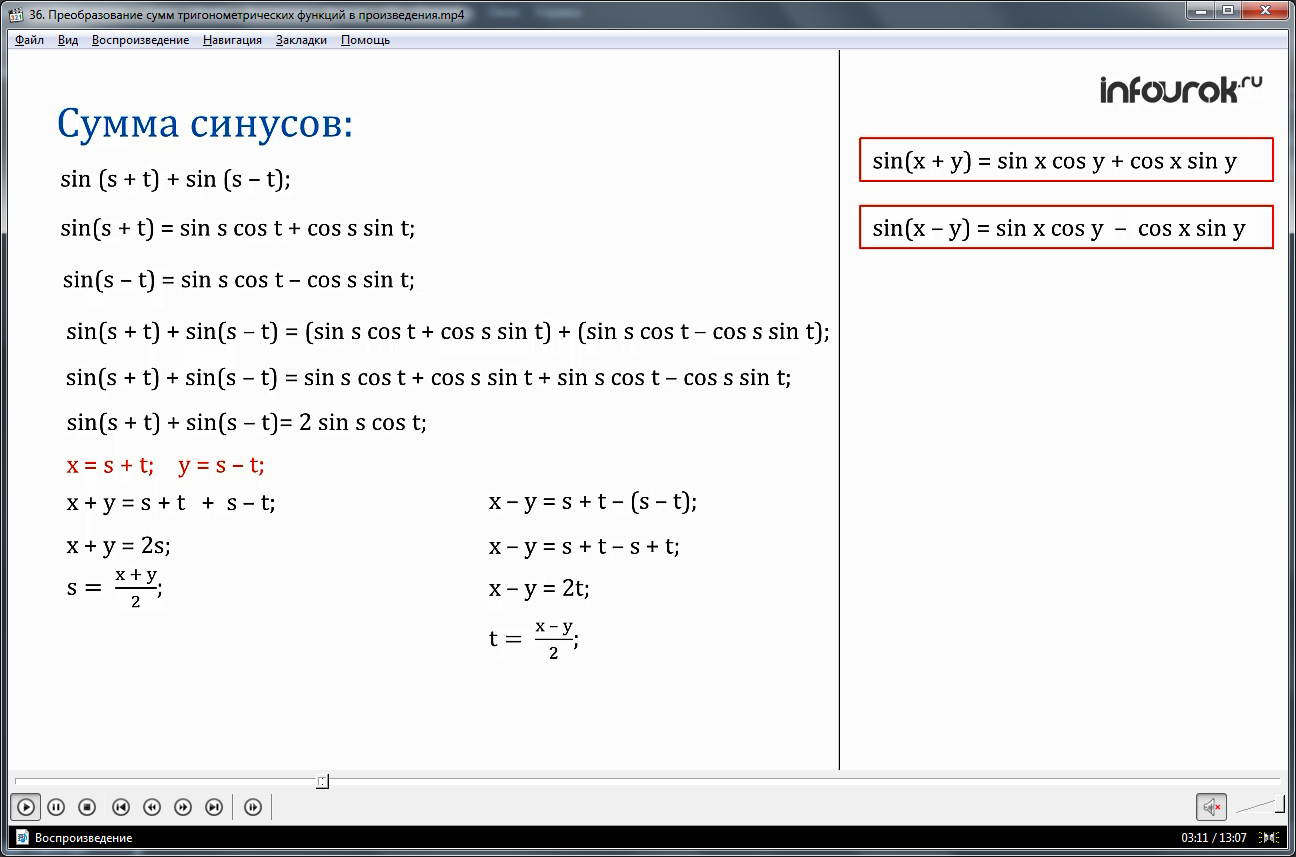
Таким образом получим, что выражение sin(s + t) + sin(s - t)= 2 sinscost.
Введем новые переменные х= s +t и у= s– t.
Сложим почленно эти равенства, то получим
х +у = s +t + s– t.
х +у = 2s
Найдем значение s
s=.
Во втором случае вычтем почленно эти равенства и получим
х -у= s + t - (s – t)
х -у= s + t - s + t
х - у = 2t
Найдем значение t
t =.
Ввыраженииsin(s + t) + sin(s - t)= 2 sin s cos t
заменим sи t на введенные нами новые переменные:
s +t заменим на х
s– t заменим на у
s на
t на .
Тогда получим:
sinх + sinу= 2 sincos
(сумма синусов двух аргументов равна удвоенному произведению синуса полусуммы этих аргументов на косинус их полуразности).
Пример.
sin 7х + sin3х =2 sin cos =2 sin5х cos2х.
Вторая формула – РАЗНОСТЬ СИНУСОВ.
Для того, чтобы мы смогли применить уже выведенную формулу суммы синусов двух аргументов sinх + sinу= 2 sincos
Воспользуемся тем, что синус – функция нечетная, т.е. - sinу = sin(- у),
sinх - sinу = sinх + sin(- у)
Теперь применим формулу суммы синусов, получим
=2 sin cos = 2 sin cos .
sin х - sin у = sin х + sin(- у) =2 sin cos = 2 sin cos .
Следовательно, получили формулу разность синусов:
sinх - sinу =2 sin cos (разность синусов двух аргументов равна удвоенному произведению синуса полуразности этих аргументов на косинус их полусуммы).
Пример. Упростить выражение sin 77° - sin 17°.
sin 77° - sin 17° =2 sin cos = 2 sin cos 47º.
(так как sin 30º= , то)= 2 ∙ ∙ cos= cos.
Третья формула – СУММА КОСИНУСОВ.
Для выражения cos (s + t) + cos (s - t) применим уже известные нам формулы косинус суммы и косинус разности:
cos (x + y) = cos x cos y - sin x sin y
cos (x - y) = cos xcos y + sin x sin y,
В выражение cos (s + t) + cos (s - t) подставим значения из формул и получим:
cos (s+ t)+ cos(s - t) = cos s cos t - sin s sin t + cos scos t + sin s sin t =2 cos s cos t
Значитcos (s+ t)+ cos(s - t) =2 cos s cos t
Введем новые переменные х= s +t и у= s – t. Как при выведении формулы СУММЫ СИНУСОВ.
s +t заменим на х
s– t заменим на у
s на
t на .
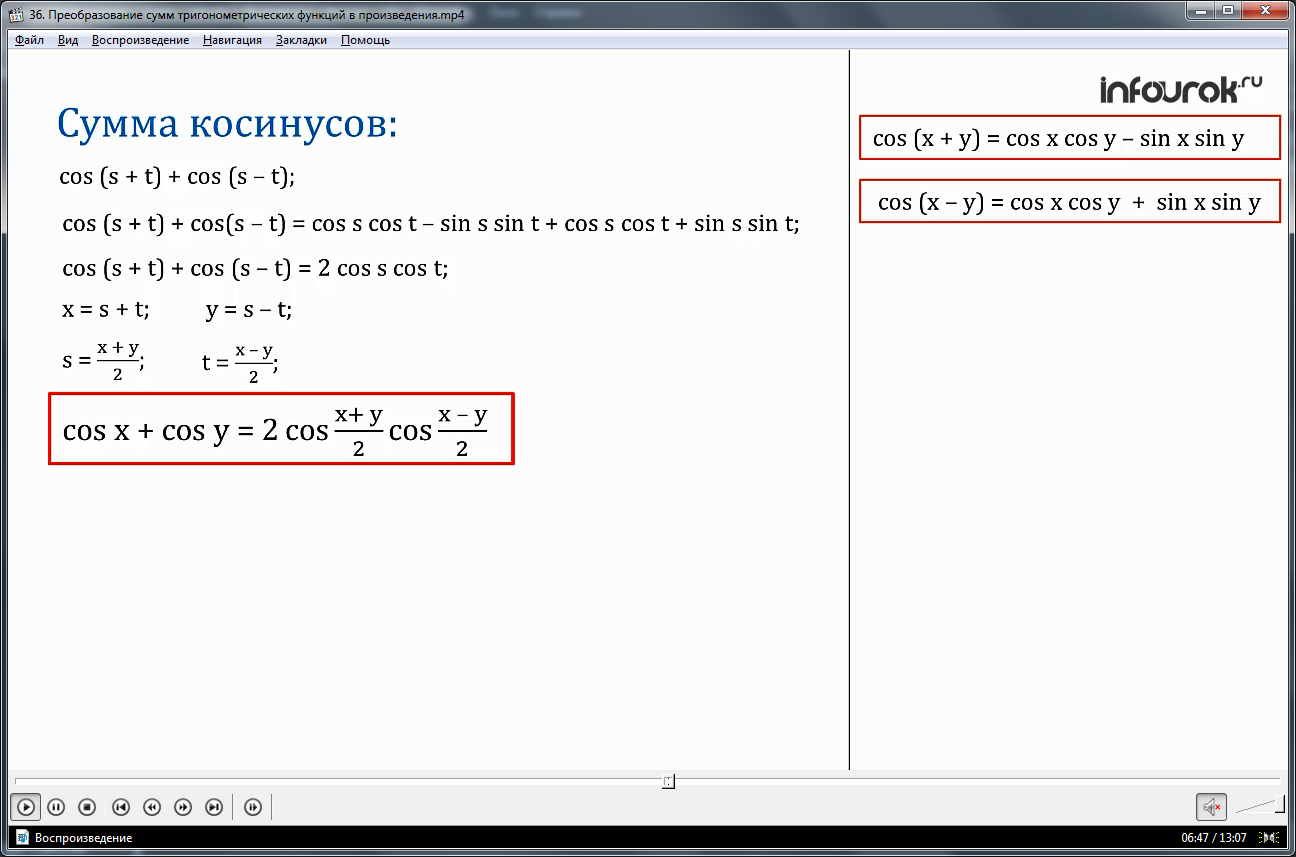
И получим формулу суммы косинусов
cos х+ cosу =2 cos cos
(сумма косинусов двух аргументов равна удвоенному произведению косинуса полусуммы этих аргументов на косинус их полуразности).
Пример. Упростить выражение cos(х+2у) + cos(3х - 2у).
cos(х+2у) + cos(3х - 2у) = 2 coscos =
=2cos 2х cos( - х + 2у)= 2cos 2х cos( -( х - 2у)) ( а так как cos( - t) = cost, то)=
= 2cos2х cos(х - 2у).
Четвертая формула – РАЗНОСТЬ КОСИНУСОВ.
Для выражения cos (s + t) - cos (s - t) применим уже известные нам формулы косинус суммы и косинус разности:
cos (x + y) = cos x cos y - sin x sin y
cos (x - y) = cos xcos y + sin x sin y, получим
cos (s+ t) - cos(s - t) = cos s cos t - sin s sin t- cos scos t - sin s sin t = - 2sin s sin t. Введемновыепеременныех= s + t и у= s – t, значит, s = иt =. Подставив введенные обозначения в формулу:
cos (s+t) - cos(s - t) = - 2sinssint, получим формулу разность косинусов:
cosх – cosу = –2sin sin (разность косинусов двух аргументов равна взятому со знаком «минус» удвоенному произведению синуса полусуммы этих аргументов на синус их полуразности).
Пример. Упростить выражение cos – cos.
cos – cos = - 2sin sin = - 2 sin sin ( таккакsin = , то)=
= - 2 ∙ ∙ sin = - sin.
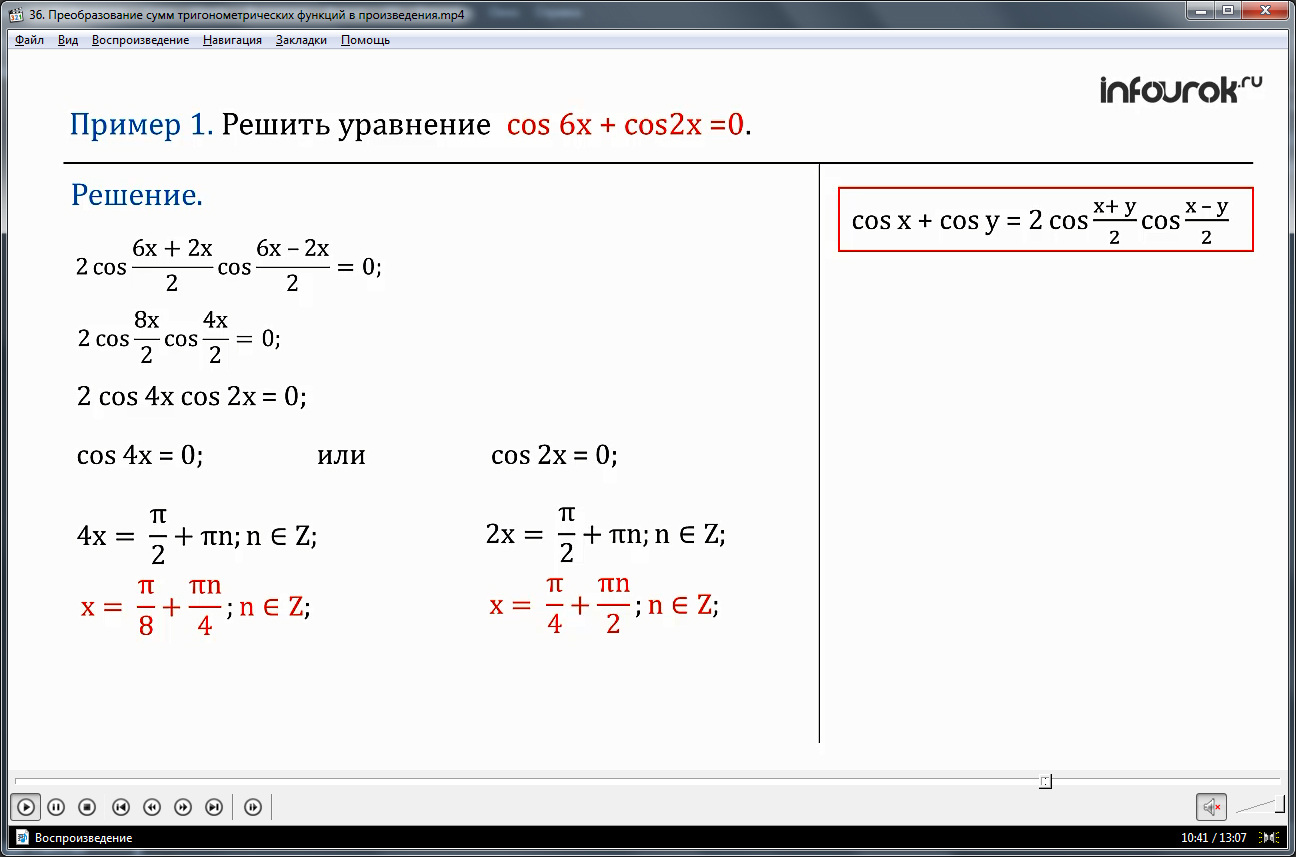
ПРИМЕР 1. Решить уравнение cos6х + cos2х =0.
Решение. Преобразовав сумму косинусов в произведение по формуле:
(cos х + cosу = 2 cos cos,
2 cos cos =0.
2 cos cos =0.
получим 2cos4х cos2х = 0. Это уравнение обращается в верное равенство, если
ПРИМЕР 2. Решить уравнение sin7х + sin3х – sin5х =0.
Решение. Для суммы первого и второго слагаемых применим формулу сумма синусов
sin(x + y) = sin x cos y + cos x sin y
имеем:
(sin7х + sin3х) – sin5х =0
2 sincos – sin5х =0
2 sin5х cos2х - sin5х =0.
Далее вынесем за скобку общий множитель sin5х и получим:
sin5х(2 cos2х – 1) = 0.
sin5х = 0 или 2 cos2х – 1 = 0,
Решений уравнения sint = a принята для а=0:
sint = 0 при t = πk,
тогда получаем
sin5х = 0
5х =πn,
х = , ( пи эн, деленное на пять)
Используя Табличные значения косинуса и определение решения уравнения cost = a, где (| а | 1) записывая в общем виде:
t = arccosа + 2πk
второе уравнение cos2х= имеет следующие решения
cos2х= .
2х= arccos + 2πn,
2х= + 2πn,
х = = + πn,
( плюс минус пи на шесть плюс пи эн).
Ответ: х = , х = + πn,
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7292 |
| Номер материала | 859 |