
Урок «Преобразование выражений, содержащих радикалы»

Краткое описание документа:
Выражения, содержащие корни, называются выражениями с радикалами, либо иррациональными выражениями. Вы уже знакомы с извлечением корня n-й степени из действительного числа. Напомним некоторые формулы для неотрицательных значений a и b.
=, (энная степень корня энной степени из а равна а) (корень энной степени из энной степени а равен а)
(Корень энной степени из произведения равен произведению корней энной степени).
- (корень энной степени из частного а на бэ равен частному корней энной степени из а и бэ)
- чтобы возвести корень энной степени в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
(Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится)
Опираясь на знания предыдущих лет и прошлых уроков, мы рассмотрим примеры на преобразование иррациональных выражений.
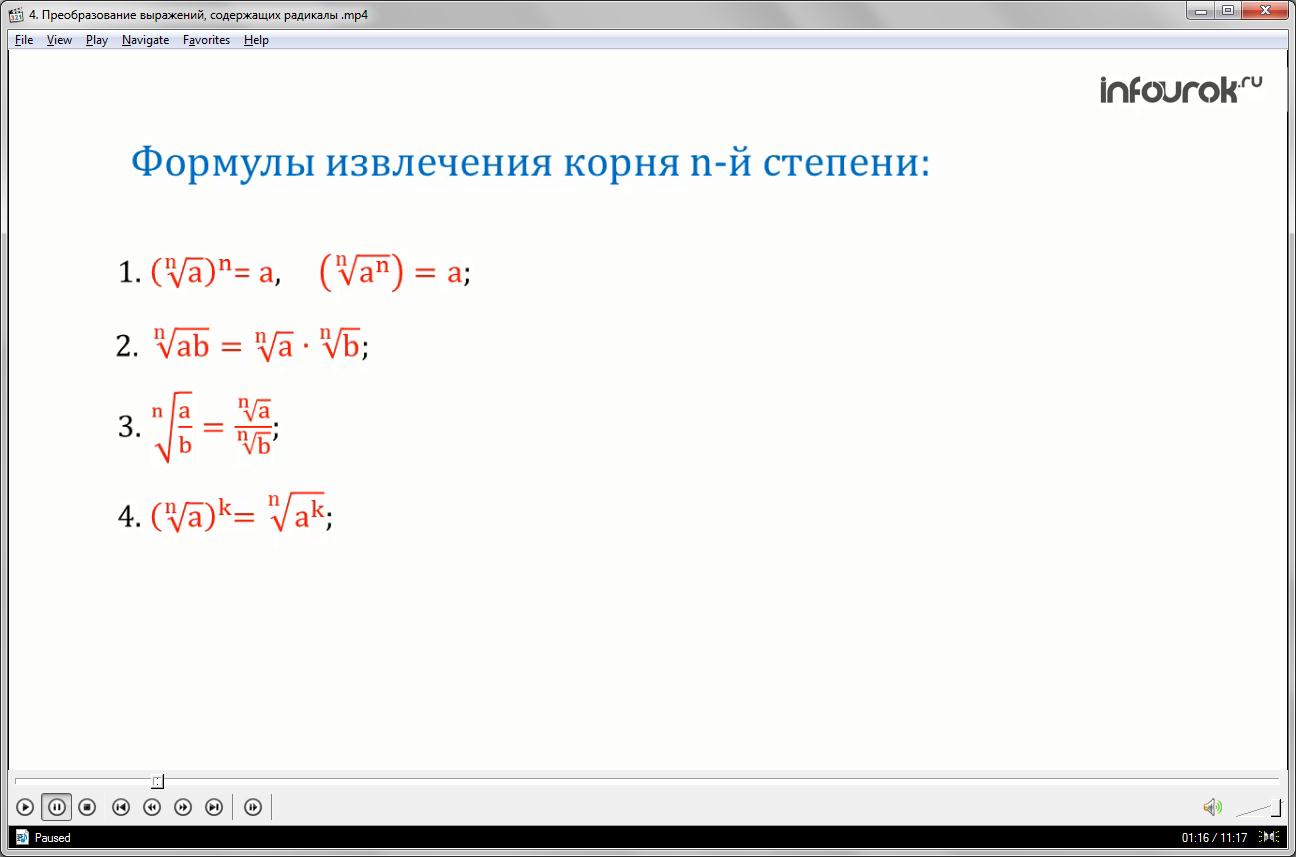
Пример 1: Упростите выражения:
Решение: подкоренное выражение разложим на множители так, чтобы корень можно было извлечь, и применим формулу (2) (Корень энной степени из произведения равен произведению корней энной степени). =
Извлечем корень кубический из 27 и =
=
Пример 1: Упростите выражение:
Решение: применим формулу (4) чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Разложим подкоренное выражение на множители так, чтобы извлекался корень:
применим формулу (2) (Корень энной степени из произведения равен произведению корней энной степени).
Из курса алгебры восьмого класса вспомним тождество (квадратный корень из а в квадрате равен модулю а) Это тождество распространяется и на случаи любого четного показателя корня (корень степени два эн из а в степени два эн равен модуль а).
Например, когда вы не уверены, что переменные принимают только положительные значения, т.е. о знаке числа а ничего не известно, необходимо рассуждать так:
== (корень шестой степени из произведения а в шестой степени на икс равно произведению корней шестой степени из а в шестой степени и икс равно произведению модуль а и корня шестой степени из икс).
Мы уже упоминали, что все формулы справедливы и выполняются в обе стороны, значит необходимо рассмотреть примеры на внесение множителя под знак радикала.
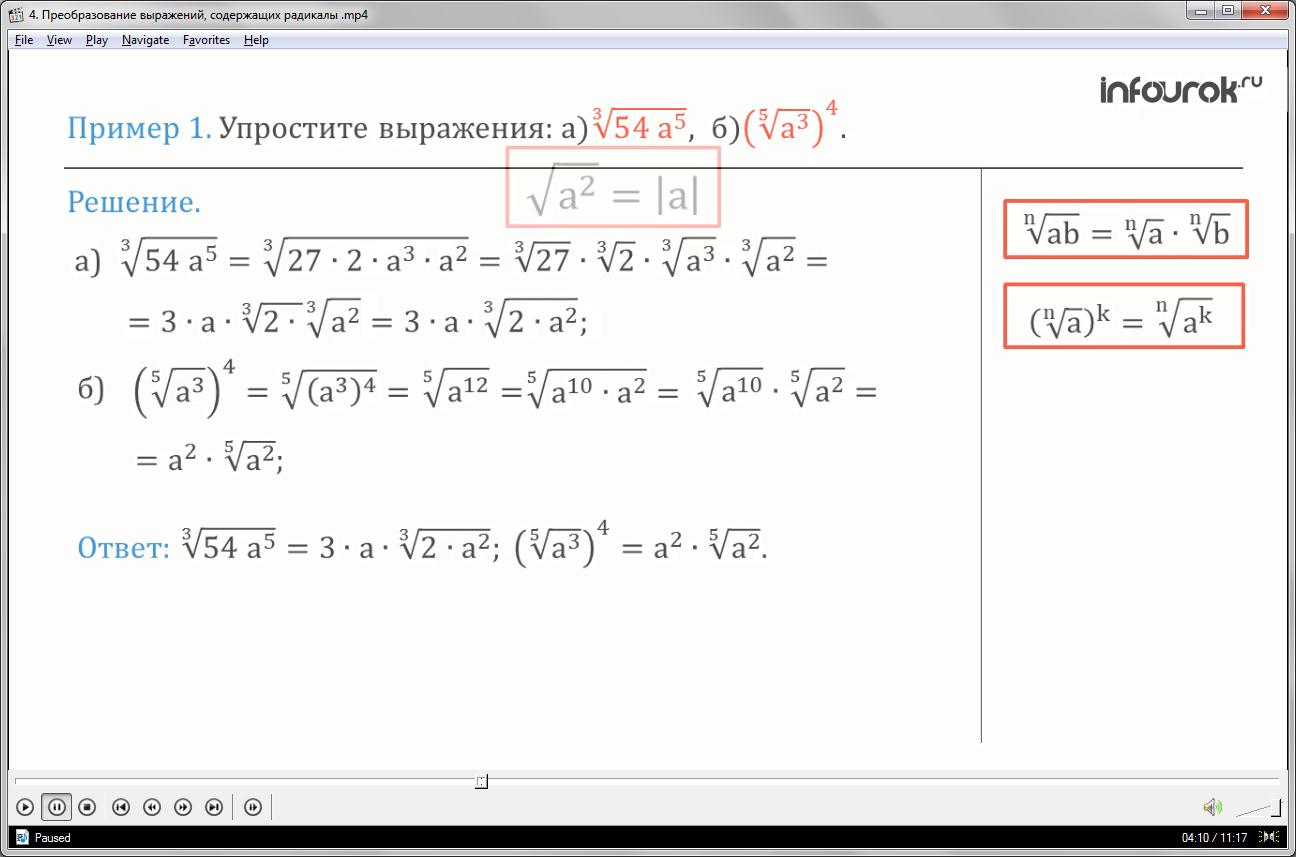
Пример 2: Сравните числа: и 5
Применим формулу (1) =, (энная степень корня энной степени из а равна а)
(корень энной степени из энной степени а равен а)
и внесем два под знак радикала, получим
а так как произведение корней равно корню из произведения, то
Преобразуем второе число.
=
Так как , то можно сделать вывод, что два корня четвертой степени из пяти меньше, чем пять корней четвертой степени из двух 5,
Пример 3: Упростите выражение
Преобразование данного выражения разобьем на два этапа.
несем множитель игрек в четвертой степени под знак корня третьей степени
(произведение корней третьей степени из куба игрек в четвертой степени и квадрата игрек) и применим формулу (2) (Корень энной степени из произведения равен произведению корней энной степени), тогда
(корень кубический из произведения игрека в двенадцатой степени и квадрата игрек равно корню кубическому из игрека в 14 степени)
Этап 2: =
Здесь применили формулу (5) (
Мы получим искомый результат (корень пятнадцатой степени из игрека в четырнадцатой).
Пример 4: Выполните действия: (произведение разности корней шестой степени из икс и из игрек на сумму этих же корней)
Решение:
Осуществим замену (корень шестой степени из икс обозначим – а, а корень шестой степени из игрек – бэ)
Применим формулу сокращенного умножения и получим:
=
(произведение разности корней шестой степени из икс и из игрек на сумму этих же корней равно разности квадратов корней шестой степени из икс и из игрек).
Применим формулу (4) чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение), получим
Применим формулу (6) (Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится) выполним действие: показатель корня и подкоренного выражения разделим на 2 и получим:
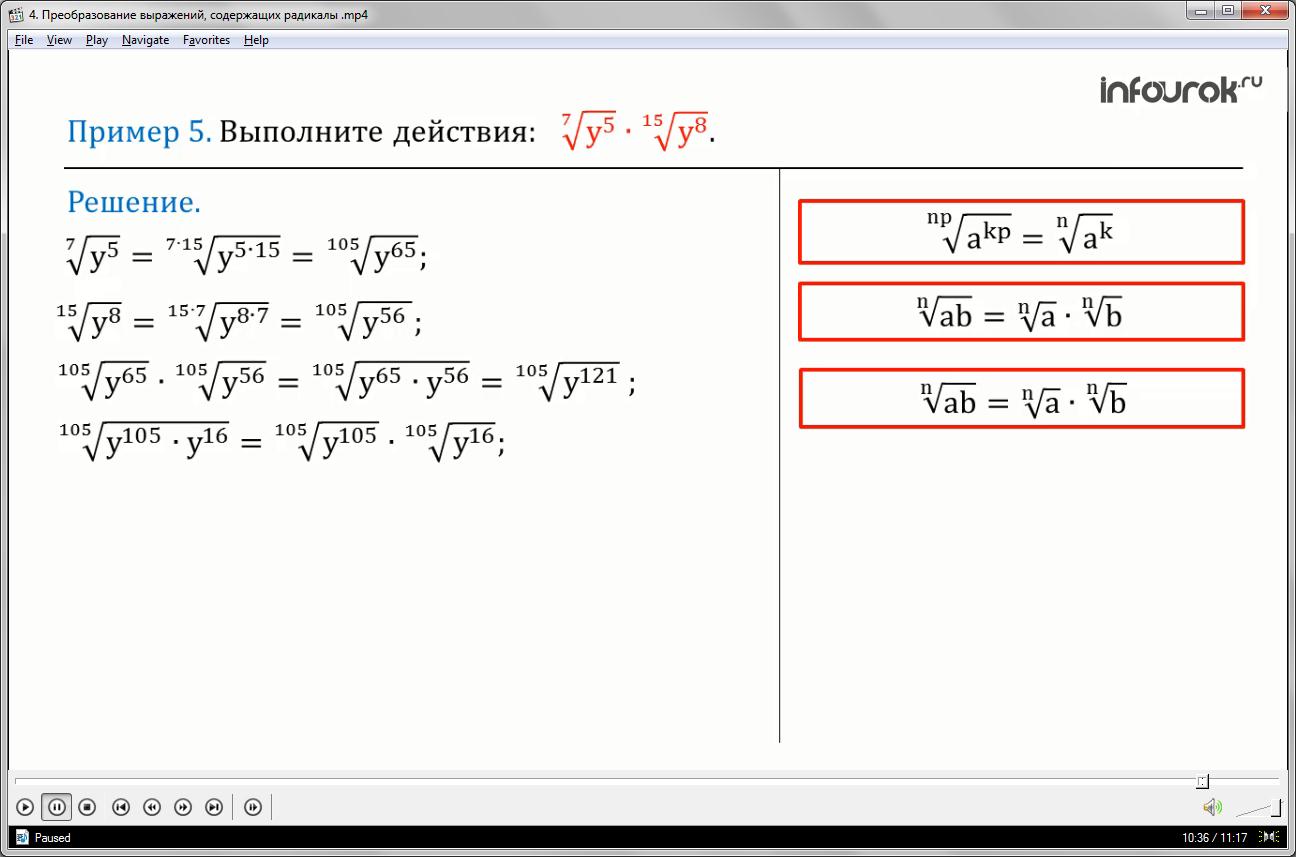
Пример 5: Выполните действия: а)
Решение: а) Так как корни различной степени, то их перемножить нельзя. Следовательно, воспользуемся (6) формулой (Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится)
и приведем их к одной степени, предварительно найдя наименьшее общее кратное двух степеней.
(корень седьмой степени из игрека в пятой степени равно корню сто пятой степени из игрек в шестьдесят пятой степени)
(корень пятнадцатой степени из игрека в восьмой степени равно корню сто пятой степени из игрек в пятьдесят шестой степени)
Воспользуемся формулой (2) (Корень энной степени из произведения равен произведению корней энной степени), тогда
(произведение корней сто пятой степени из игрека в 65 степени и игрека и 56 степени равно корню сто пятой степени из произведения игрека в 65 степени и игрека и 56 степени, равно корню сто пятой степени из игрека в сто двадцать первой степени).
Вынесем множитель из под знака корня, для этого разложим подкоренное выражение на множители =
и применим формулу (2) (Корень энной степени из произведения равен произведению корней энной степени):
(корень сто пятой степени из произведения игрек в 105 степени и игрек в 16 степени равно произведению корней 105 степени из игрек в 105 степени и игрек в 16 степени)
Применим формулу:
и получим, что
(произведение корней 105 степени из игрек в 105 степени и игрек в 16 степени равно произведению игрека на корень 105 степени из игрека в 16 степени).
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6950 |
| Номер материала | 1053 |