
Урок "Преобразование выражения A sin x + В cos x к виду С sin(х + t)"

Краткое описание документа:
Видеоурок «Преобразование выражения Asin x + Вcos x к виду Сsin(х + t)» сопровождается спокойным точным голосом диктора, который объясняет и комментирует урок и примеры, рассматриваемые в ней. В электронном обучающем ресурсе приводятся две части. В первой из них рассматривается теория, объясняются формулы и получения данных формул, рассказывается их применение на практике, а во второй – показывается практическое применение.
Данный видеоурок «Преобразование выражения Asin x + Вcos x к виду Сsin(х + t)» можно продемонстрировать во время, непосредственно, урока. Таким образом, он станет более насыщенным и понятным как можно большему количеству школьников. Для каждого учителя важно привлечь внимание школьников, заинтересовать новой темой, что является залогом успешного урока.
При решении некоторых примеров появляется необходимость привести Asin x + Вcos x в вид Сsin(х + t). Это поможет сократить габаритные выражения, что приведет к быстрому выполнению решения того или иного примера.
Как известно, тригонометрические выражения могут возникнуть не только при решении математических задач, но и в физике, механике и т.д.
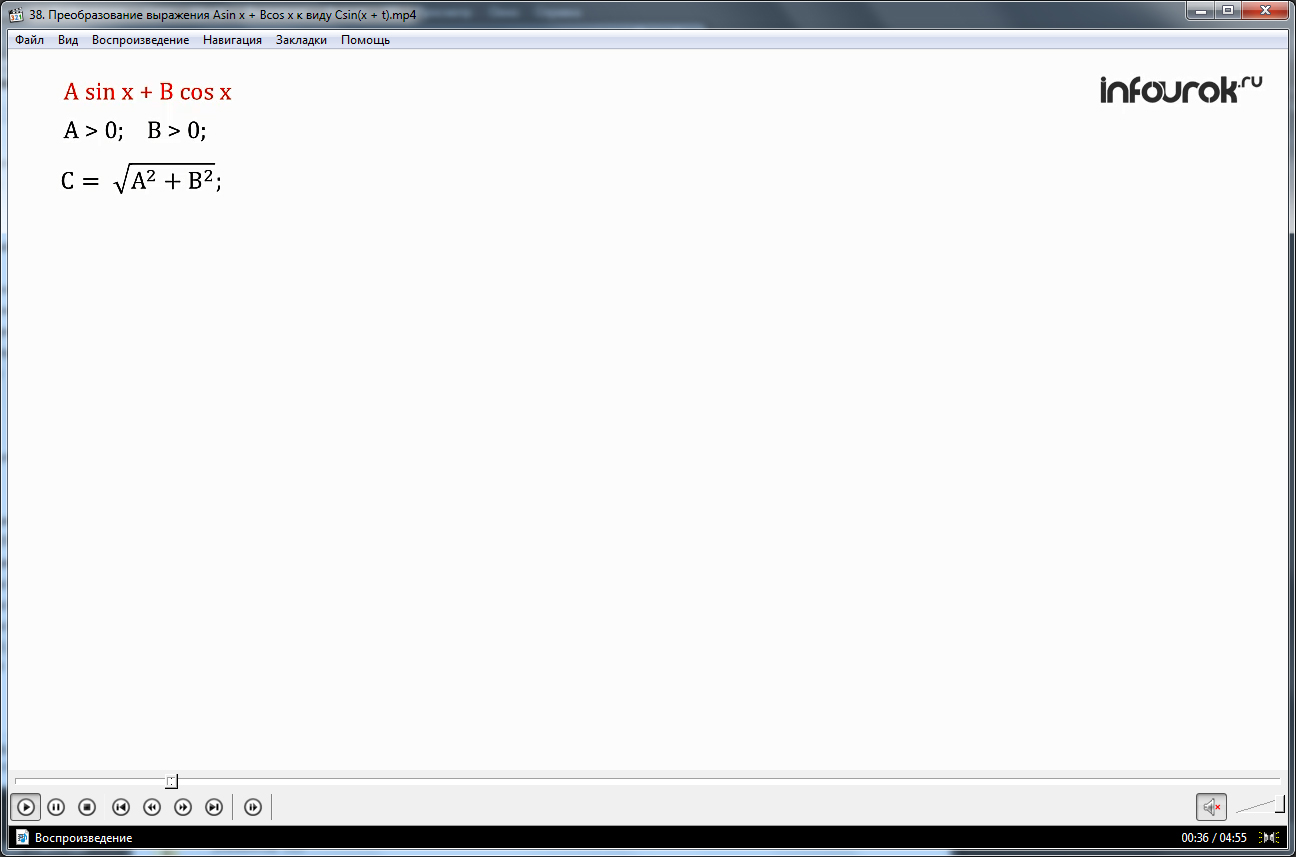
Для начала выводится на экран выражение, над которым в дальнейшем придется поработать. Заранее указывается, что коэффициенты являются больше нуля. В случае равенства нуля смысл выражения будет утрачен. Итак, A и B больше 0.
Коэффициент C предположительно равняется корню из суммы квадратов А и В. Если учесть основное тригонометрическое тождество, то сумма х и у к квадрате будет равняться единице. Выполнив замену, подставляя вместо х и у полученные дроби, образовывается новое выражение
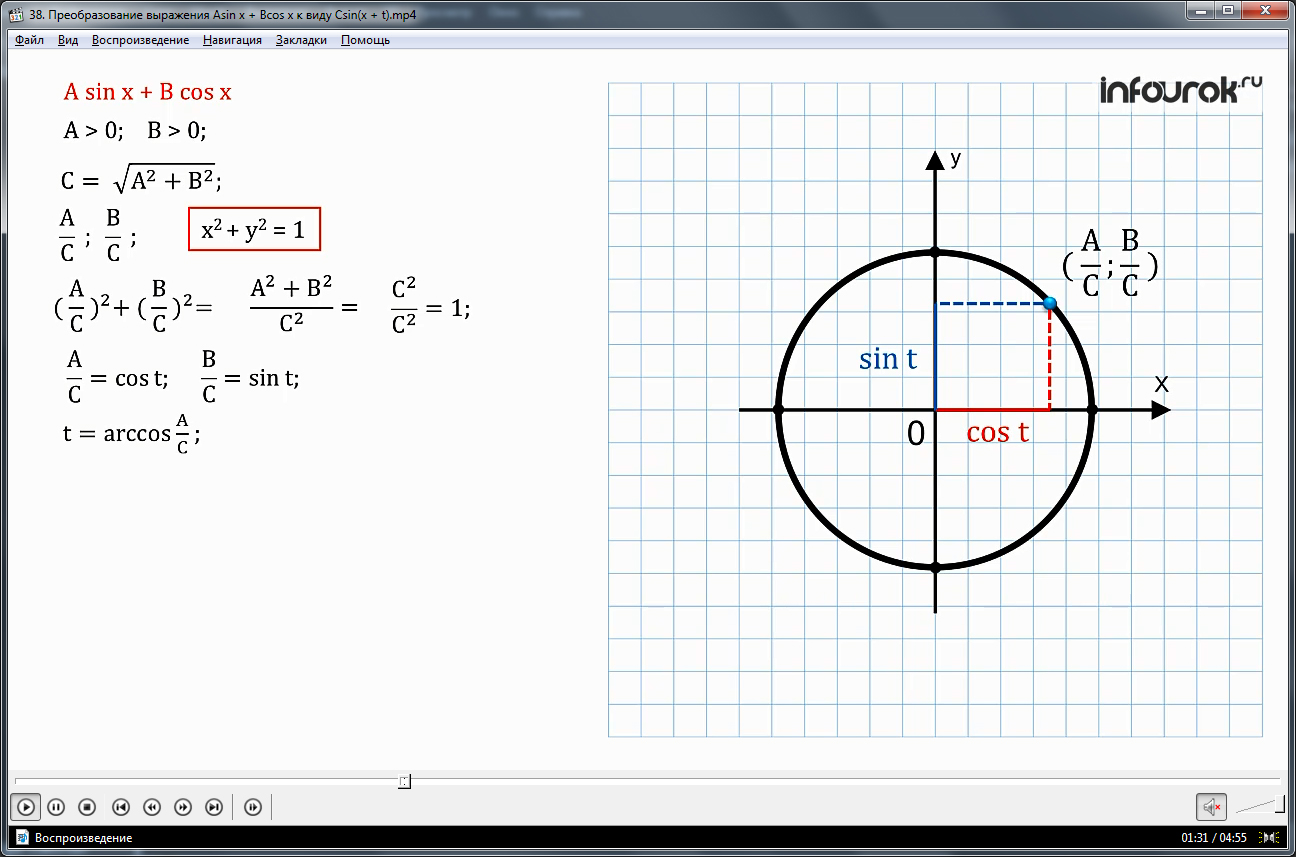
Смысл данного алгебраического выражения выводится на экране геометрическим путем на единичной окружности.
Выполнив замену через тригонометрические синус и косинус от аргумента, получаем полноценное тригонометрическое выражение. Далее появляются обратные тригонометрические функции арксинус и арккосинус, при выводе аргумента. В результате применения уже изученных формул ранее, получается еще одна формула, с которой в дальнейшем придется научиться работать и применять при решении практических занятий.
Далее диктор объясняет, как аналогичным образом вывести формулу для случая разности. При этом указывается также, что коэффициенты не могут быть меньше либо равняться нулю.
В видеозаписи далее начинается рассматривание практических примеров, с помощью которых можно закрепить изученный теоретический материал. Первый пример предлагает преобразовать некоторое выражение, которое представляет собой сумму двух тригонометрических функций. Для того чтобы решить данный пример, необходимо вспомнить изученные на этом и предыдущих уроках тригонометрические функции и их основные свойства.
Диктор подробно комментирует и объясняет каждый шаг при выведении решений на экране. С помощью данного видеоурока школьники могут понять принцип решения подобных примеров, которые могут встречаться как в домашнем задании, так и на контрольных или самостоятельных работах.
Итак, данный электронный ресурс можно скачать на данном сайте для проведения наиболее эффективного урока, над которым будет работать в дальнейшем.
ТЕКСТОВАЯ РАСШИФРОВКА:
Преобразование выражения A sin x + B cos x к виду C sin(x + t)
Разберем прием введения вспомогательного аргумента.
Пусть дано выражение A sinx + B cosx( а синус икс плюс бэ косинус икс) и для определенности A0 и B0. Введем обозначение С =
(сэ равно квадратный корень из суммы квадратов а и бэ). Пара чисел
( а, деленное на сэ) и ( бэ, деленное на сэ) удовлетворяет уравнению окружности х2 + у2 = 1, так как ( )2 + ( )2 = = = 1. Это значит, что точка с координатами ( ; ) лежит на единичной окружности. Но абсцисса точки - это косинус некоторого аргумента t, а ордината точки - это есть синус аргумента t, то есть = cos t, а = sin t. Следовательно,
t = arccos (тэ равно арккосинус а, деленное на сэ),
t = arcsin (тэ равно арксинус бэ, деленное на сэ).
Умножим и разделим выражение A sinx + B cosx на С:
С ∙ ( ∙ sinx + ∙ cosx) = С ∙ ( ∙ sinx + ∙ cosx) =
(применяя формулу синус суммы: sin(x + y) = sinxcosy + cosxsiny, получим)
= C sin(x + t).
Таким образом, A sinx + B cosx = C sin(x + t), где С = , t = arcsin.
Аргумент t называют вспомогательным (или дополнительным) аргументом.
Выражение A sinx - B cosx, где A0 и B0 аналогично можно преобразовать к виду C sin(x- t).
Рассмотрим примеры.
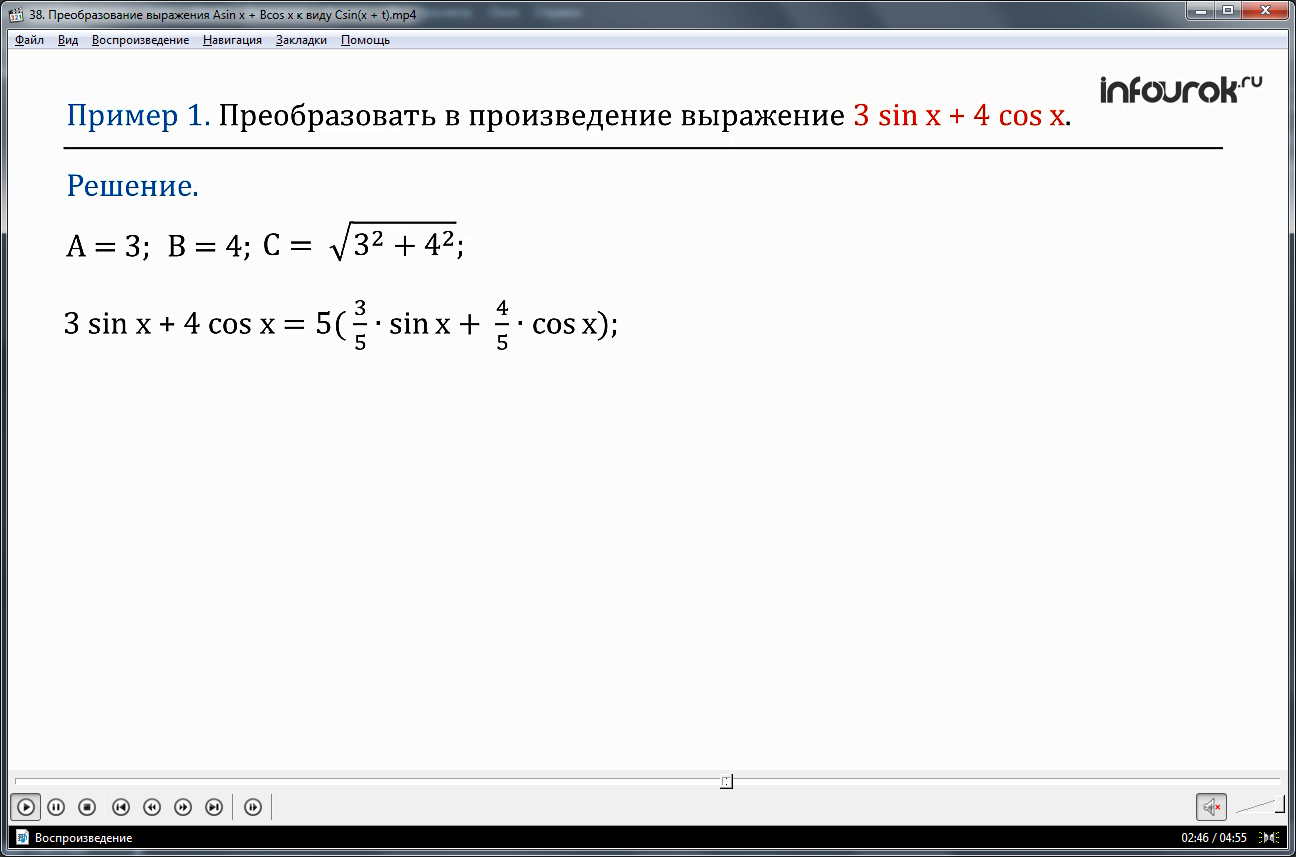
ПРИМЕР 1. Преобразовать в произведение выражение 3sinx + 4cosx.
Решение. В нашем случае А = 3, B = 4, С = = 5. Получили
3sinx + 4cosx = 5( ∙ sinx + ∙ cosx).
Введем вспомогательный аргумент t, который удовлетворяет равенствам:
cos t= , sin t = , и равен, t = arcsin ( тэ равно арксинус четырех пятых).
Следовательно, 3sinx + 4cosx = 5 sin(x + t), где t = arcsin.
Ответ: 5 sin(x + t), где t = arcsin.
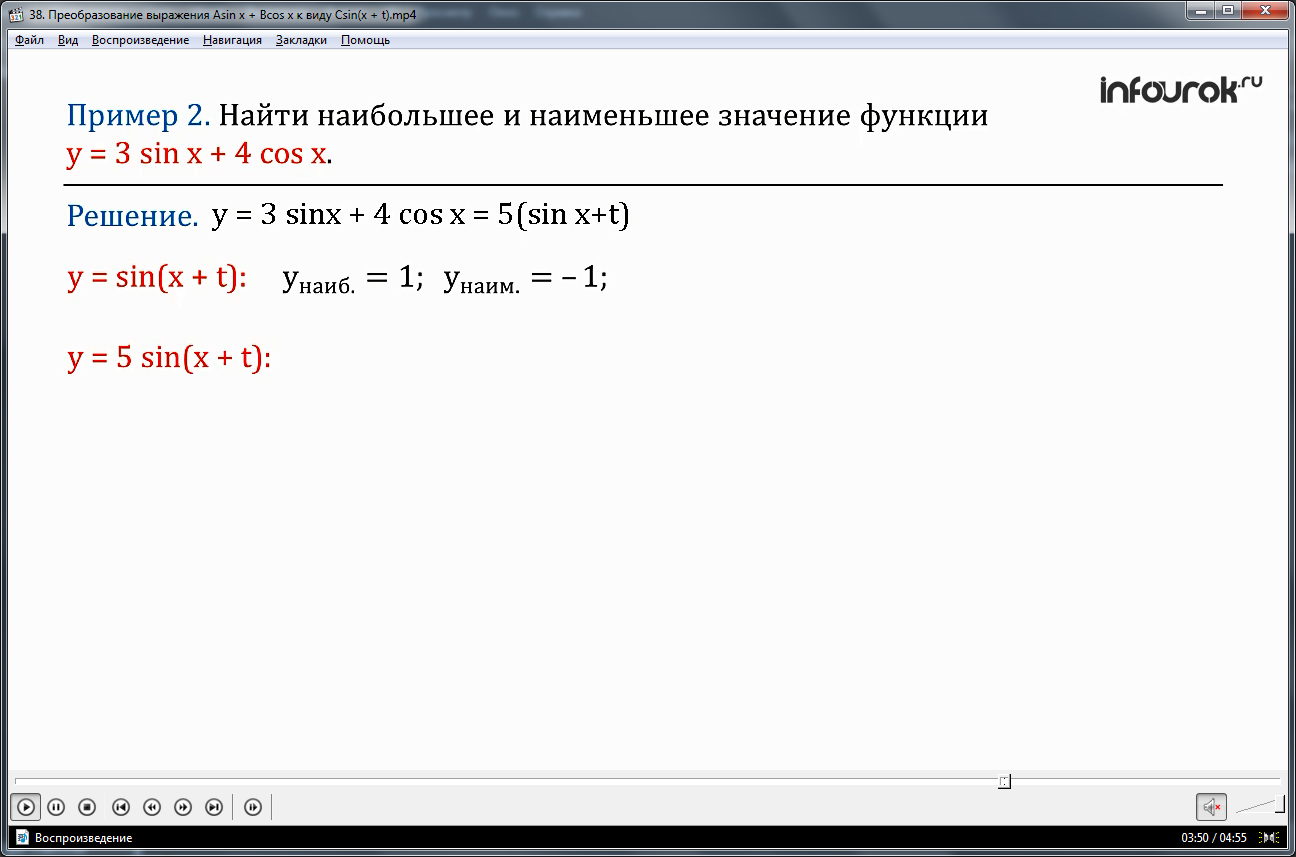
ПРИМЕР 2. Найти наибольшее и наименьшее значение функции
у=3sinx + 4cosx.
Решение. Используя пример 1, имеем у=3sinx + 4cosx=5 sin(x + t).
Поскольку наибольшим значением функции у = sin(x + t) является число 1, а наименьшим – число -1(минус один), то наибольшим и наименьшим значениями функции у = 5 sin(x + t), а значит, и данной функции будут соответственно числа 5 и -5: унаиб.=5, унаим.= -5.
Ответ: унаиб.=5, унаим.= -5.
ПРИМЕР 3.Решить уравнение 3sinx + 4cosx = 5.
Решение. Преобразуем левую часть уравнения (используя пример 1) к виду
5 sin(x + t), гдеt = arcsin . Имеем:
5sin(x + t) =5,(разделим на 5 обе части уравнения)
sin(x + t) =1,
x + t = + 2πn,
х = - t + 2πn, , где t = arcsin.
Ответ: х = - arcsin + 2πn, .
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13018 |
| Номер материала | 861 |