
Урок "Преобразования графиков тригонометрических функций из y=f(x) в y=mf(x)"

Краткое описание документа:
Данный видеоурок по алгебре для 10-го класса познакомит слушателей с преобразованием графиков тригонометрических функций из у=f(x) в y=mf(x).
В начале урока дается информация о том, что ранее учащиеся научились строить различные графики функций, которые получаются из графика функции у=f(x) путем параллельного переноса относительно оси х или относительно оси у.
В данной теме описаны этапы процесса построения графика y=mf(x) из графика у=f(x) при условии, что m – действительное число, не равное нулю.
В первом варианте рассматривается, каким образом строится график функции y=mf(x), когда m - положительное число. В данном случае происходит растяжение графика от оси х с коэффициентом m, а при 0<m<1 – сжатие к оси x с коэффициентом 1/m. Точки пересечения с осью х остаются на месте,
В качестве примеров в видеоуроке показаны:
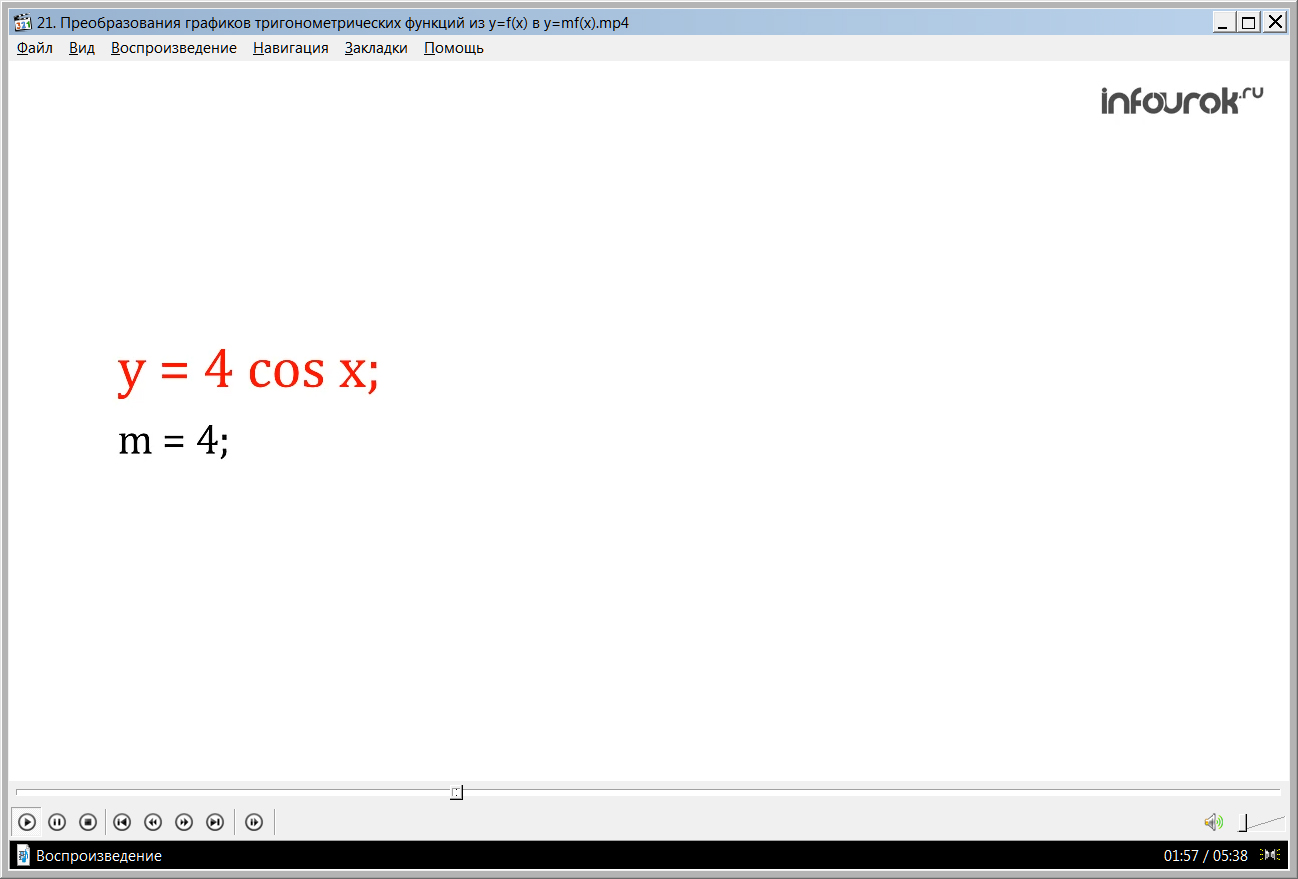
1) построение графика у = 4cosx. Вначале строится график у = cosx. Т.к. в данном случае m = 4, выполняется растяжение графика от оси х на 4 единицы.
2) построение графика у = 0,5sinx. Также сначала строится график у = sinx, который преобразовывается в у = 0,5sinx путем сжатия к оси х с коэффициентом 0,5. Точки пересечения с осью абсцисс снова остаются на месте.
Во втором варианте автор рассматривает построение графика функции y=mf(x), если m отрицательное число. Например, при m = –1 функция y=mf(x) = –f(x). В таком случае ординаты точек функции y = –f(x) отличаются от исходной функции y=mf(x) только знаком, что показано на соответствующем рисунке: точки функций симметричны относительно оси абсцисс.
На следующем рисунке даны графики функций у = sinx и у = –sinx. График функции у =–sinx получается из графика функции у = sinx путем преобразования симметрии относительно оси х.
Далее рассматривается последовательность построение графика функции y=mf(x) при m<0 на примере функции у = – 2,5cosх:
1) строится одна волна графика у = cosх;
2) т.к. m=2,5, выполняется растяжение волны графика от оси х на 2,5 единицы;
3) т.к. m<0, производится преобразование симметрии относительно оси х. Достраивая волну, получается весь график функции у = – 2,5cosх.
Видеоматериал будет удобен при самостоятельном изучении темы, так как сочетает доступное изложение теоретической части с приведением и объяснением практических задач.
Использование видео на уроке даст возможность учителю привлечь учеников современной подачей программного материала.
В результате детального и последовательного прослушивания видео, ученики с легкостью запомнят основные моменты преобразований графиков тригонометрических функций, таких как сжатие и растяжение относительно оси х, преобразование симметрии относительно оси х.
ТЕКСТОВАЯ РАСШИФРОВКА:
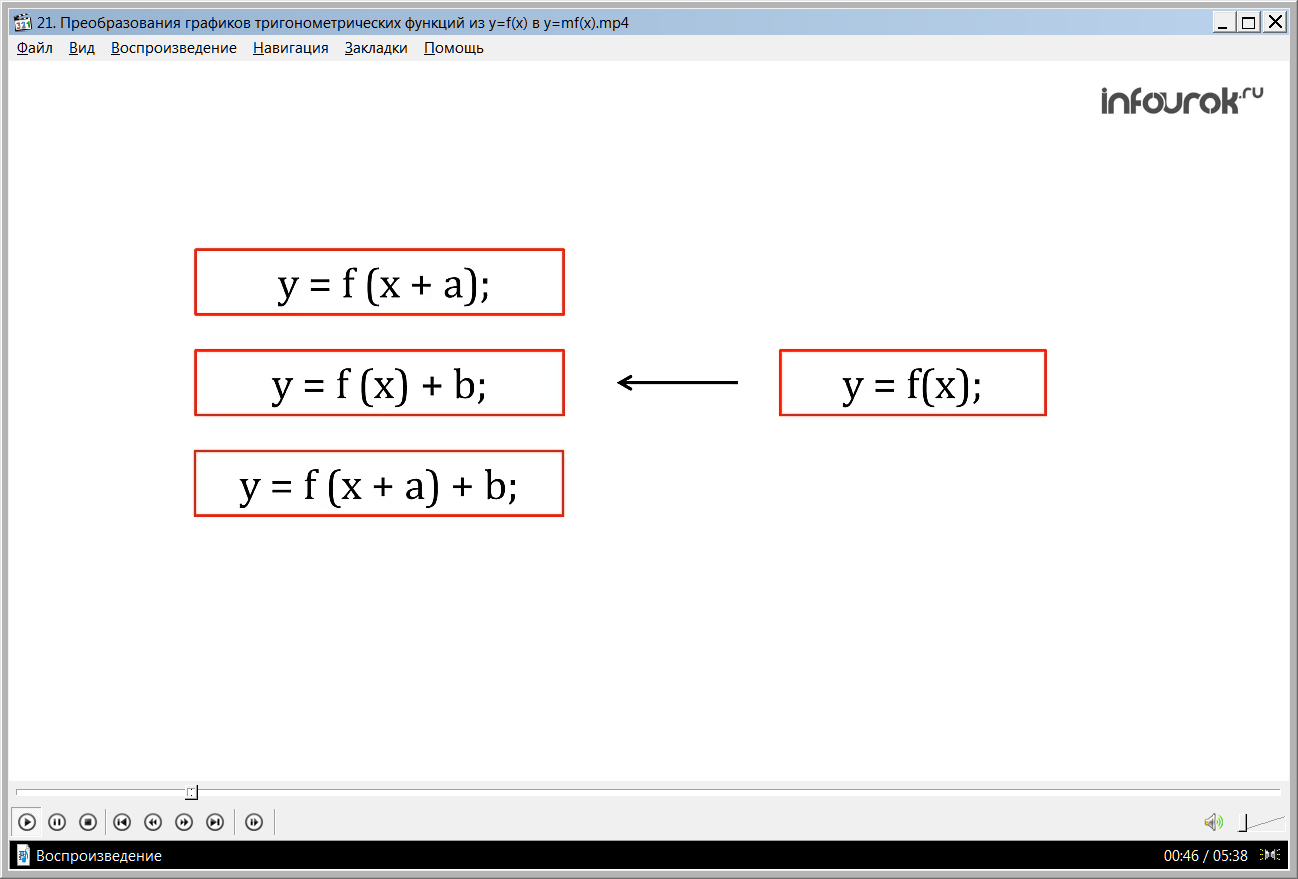
На уроках алгебры в 8 и 9 классах мы научились строить графики функций
у = f (x + а), у = f (x) + b, у = f (x + а) + b ( игрек равно эф от аргумента икс плюс а, игрек равно сумме эф от аргумента икс и бэ, игрек равно сумме эф от аргумента икс плюс а и бэ) и знаем, что все они получаются из графика функции у = f(x) путем преобразования параллельного переноса на |а|
( модуль а) единиц вправо или влево вдоль оси х и на | b|(модуль бэ) единиц вверх или вниз вдоль оси у. Сегодня мы научимся по графику у = f(x) строить график у = mf(x), где m – любое действительное число (кроме нуля).
1) Рассмотрим построение графика функции у = mf(x), когда m – положительное число.
Чтобы получить ординаты точек графика функции у = mf(x), нужно умножить ординаты соответствующих точек функции на число m. Обычно, такое преобразование называют растяжением от оси х с коэффициентом m. При таком преобразовании на своем месте остаются только точки пересечения с осью х. Если же m меньше единицы, то говорят о сжатии к оси х с коэффициентом ( единица деленное на эм). Например, если m = ( эм равно одной седьмой), то говорят о сжатии с коэффициентом 7.
Построим график функции у = 4cos x. Так как m = 4, график функций у = 4cosx выполняем растяжением графика функции у = cosx от оси х. На своем месте остаются только точки пересечения графика у =cosx с осью х, по оси у растягиваем график на коэффициентом m, т.к. m=4, то на растягиваем на 4 единицы.
Чтобы выполнить график функции у = 0,5sin x, построим график функции у = sin x, преобразуем его. На своем месте остаются только точки пересечения с осью х. Так как m меньше единицы, то сожмем его к оси х с коэффициентом .
2) Рассмотрим построение графика функции у = mf(x), когда m = – 1
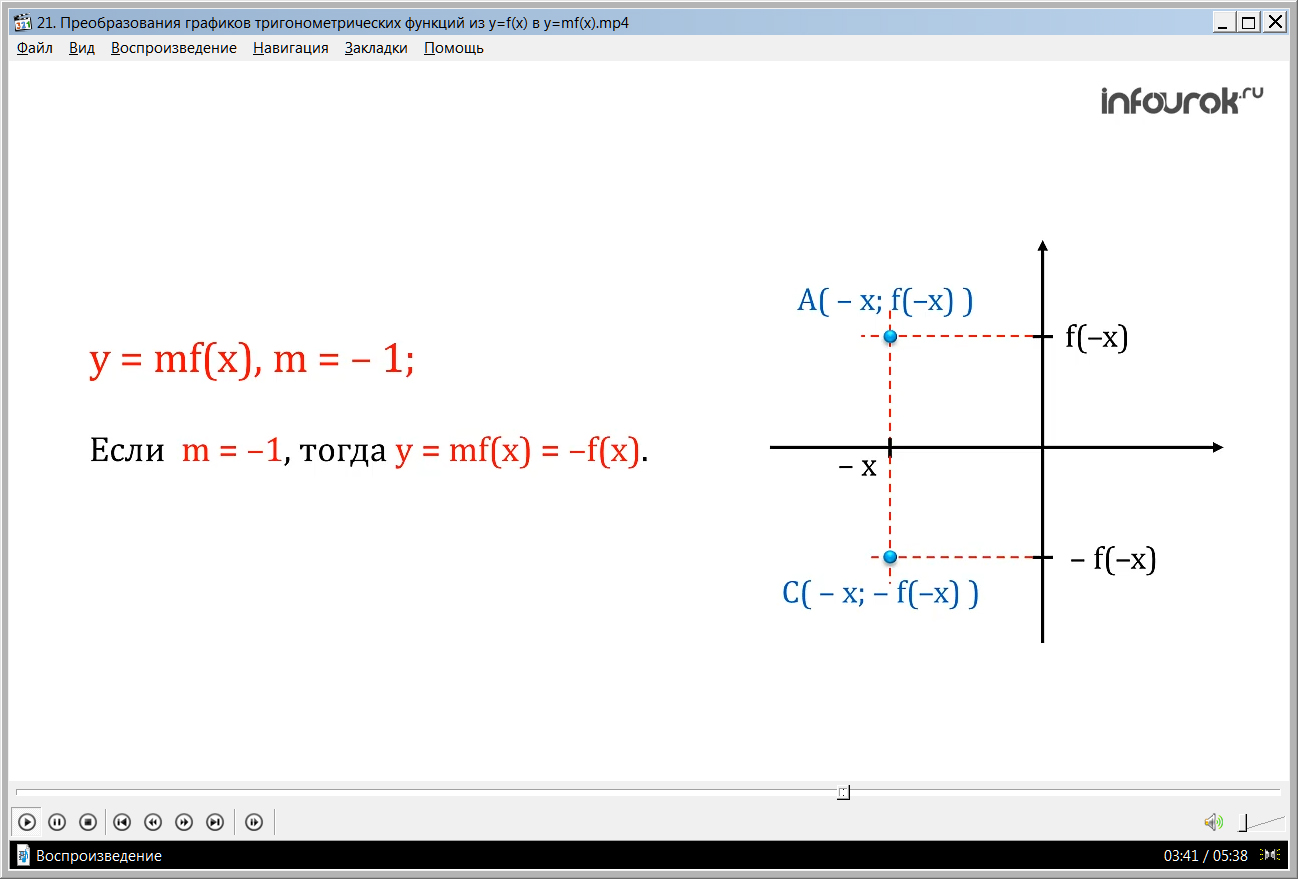
Если m = - 1, значит функция у = mf(x) будет равна функции у = - f(x).
Очевидно, что ординаты точек графика функции у = - f (x) отличаются только знаком от соответствующих ординат точек графика функции у = f (x).
Это значит, что точки А( – х: f(–x)) и С( –х: – f(–x)) ( а с координатами минус икс и эф от минус икс и сэ с координатами минус икс и минус эф от минус икс симметричны относительно оси абсцисс. ( смотри рис 3).
Следовательно, чтобы построить график функции у = - f(x), нужно к графику функции у = f(x) применить преобразование симметрии относительно оси абсцисс. На рисунке 4 изображены графики функций
у = sin x и у = - sin x.
3)Чтобы построить график функции у = mf(x), если m – отрицательное число, нужно помнить, что справедливо равенство mf(x) = – |m|f(x) ( эм, умноженное на эф от икс равно минус модуль эм , умноженное на эф от икс), то фактически нам нужно построить график функции у = – |m|f(x). А это можно сделать последовательно:
во-первых, построить график функции у = f(x);
во- вторых, подвергнуть его растяжение от оси х с коэффициентом |m|;
в-третьих, к полученному графику применить преобразование симметрии относительно оси абсцисс.
Применим данный алгоритм на практике.
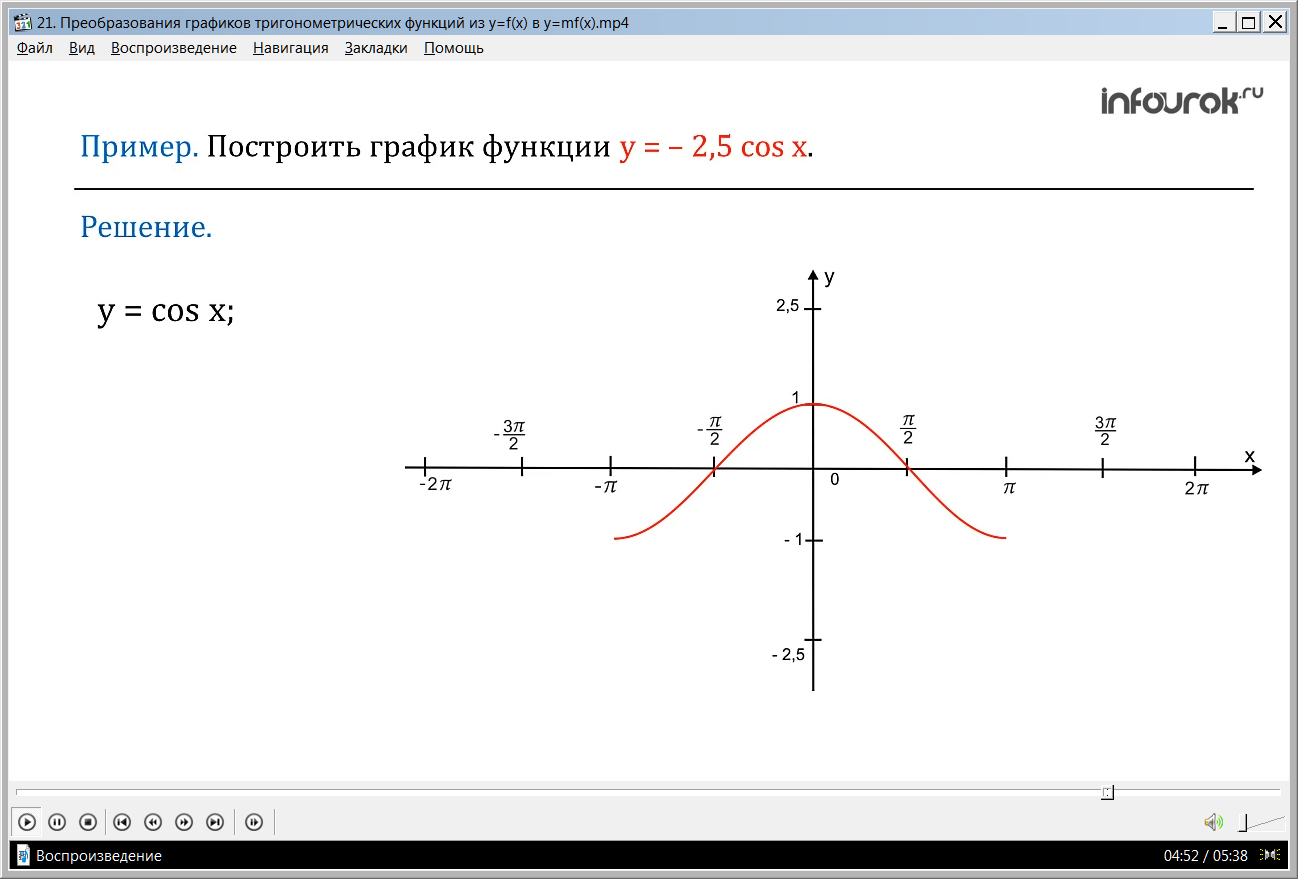
ПРИМЕР. Построить график функции у = - 2,5 cos x ( игрек равно минус две целые пять десятых, умноженное на косинус икс).
Решение. Построим одну волну графика у = cos x ( рис.5).
Далее осуществим растяжение построенного графика от оси х с коэффициентом 2,5 и получим одну волну графика функции у = 2,5 cos x (рис.6)
Затем к построенной волне графика функции у = 2,5 cos x применим преобразование симметрии относительно оси абсцисс, получим волну графика функции у = – 2,5 cos x( рис.7). И, наконец, с помощью волны получим весь график функции у = - 2,5 cos x. ( рис.8) двигая его вправо и влево на 2
Комментарий:
необходимо строить всю волну графика синусоиды или косинусоиды, так как в результате по преобразованиям мы бы получили полу волну, и не ясно было как получен весь график у= –2,5 cosx
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6211 |
| Номер материала | 849 |