
Урок "Приближенные значения действительных чисел"

Краткое описание документа:
Данный видео урок познакомит вас с темой «Приближенные значения действительных чисел». Ранее в наших видеоматериалах, знакомя вас с другими темами, были приведены примеры с более легкими «хорошими» корнями. Но так бывает далеко не всегда. Сегодняшний урок мы посвятим рассмотрению значения приближенных действительных чисел, а также познакомимся со способами и видами их получений.
Существует ряд причин, по которым используют приближенные значения действительных чисел. Среди них можно встретить: неудобство использования бесконечных десятичных дробей чисел, при решении графических задач приблизительное определение корней, когда невозможно установить точное значение и прочее.
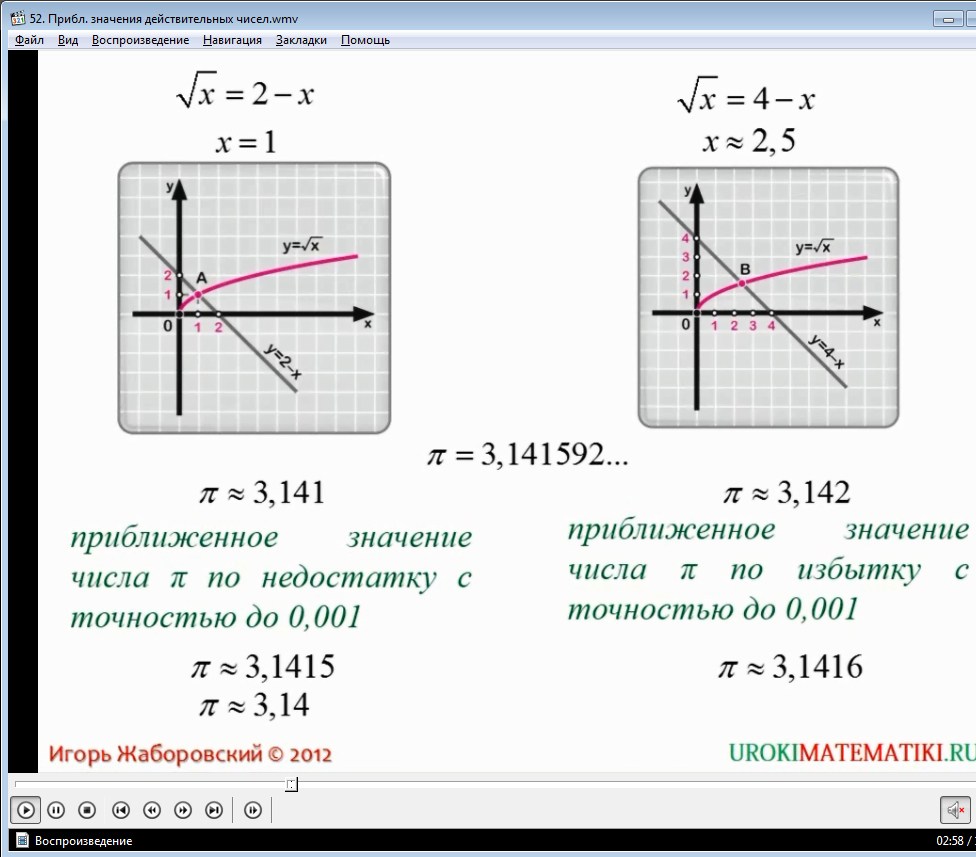
Например, для цифрового обозначения числа p, которое является бесконечным и равно 3,141592….. до бесконечности, если же пользоваться приближенными равенствами, то это число может иметь значение 3,141 или 3, 142. Первое называют приближенным значением числа p по недостатку с точностью до 0,001; второе называют приближенным по избытку с той же точностью. Более подробно смотрите в представленном материале.
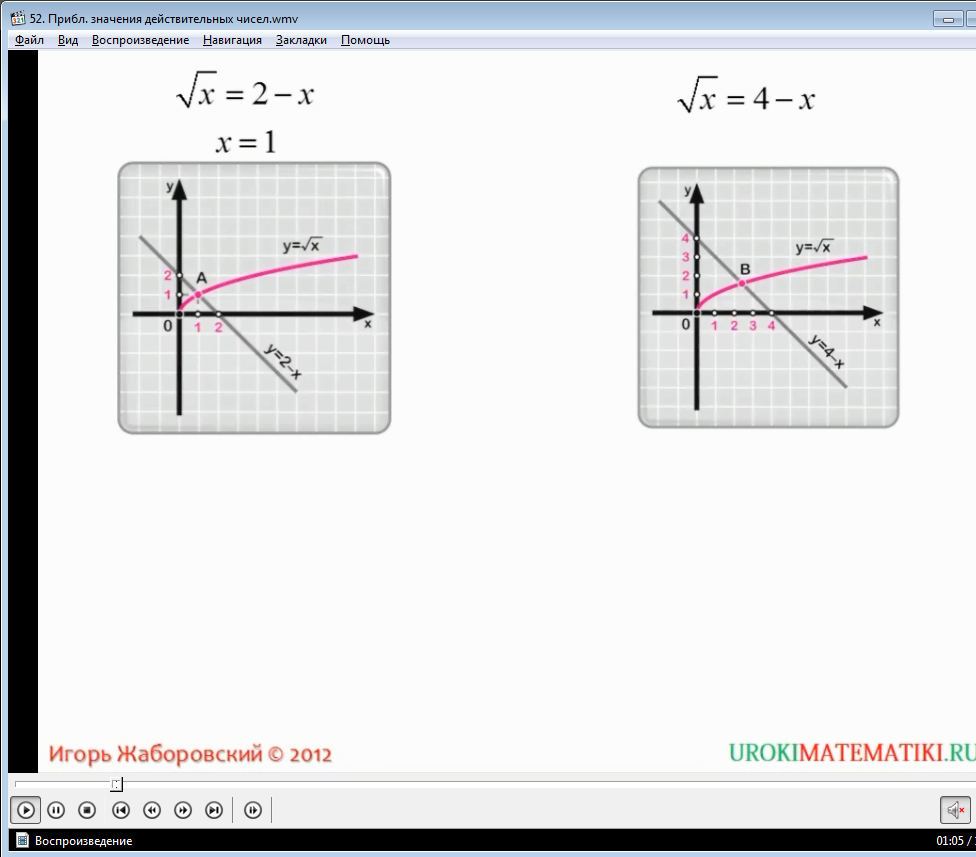
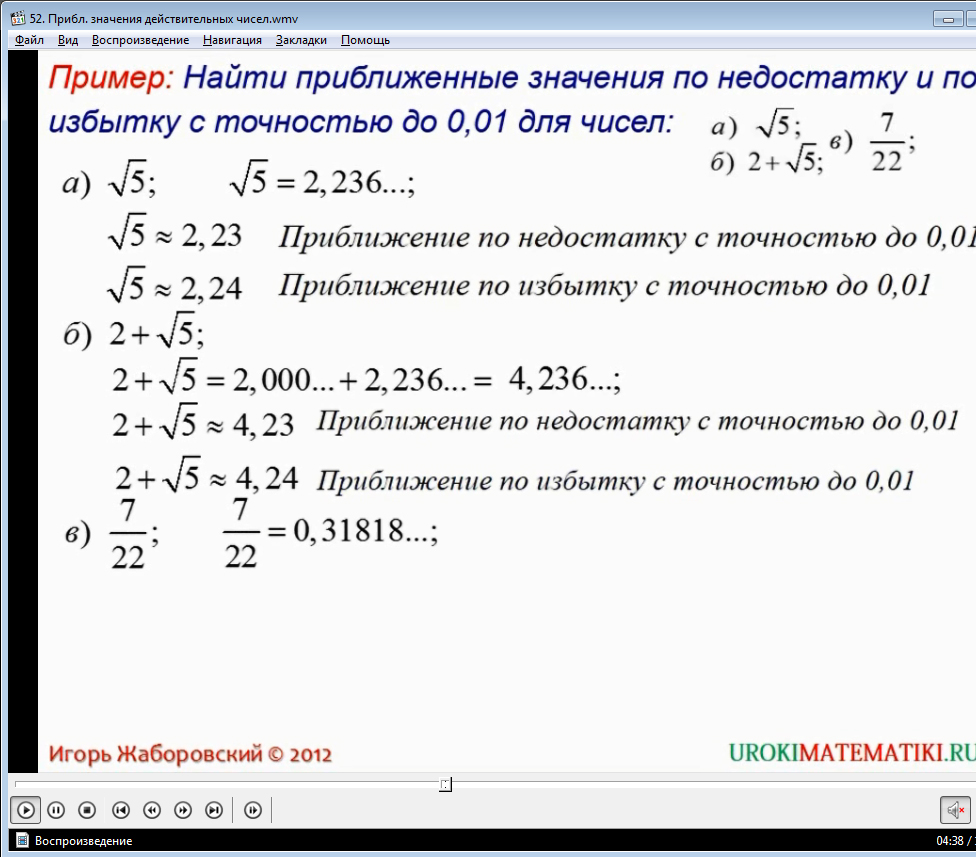
Рассмотрим далее, предложенном в видео, на примере: найти приближенные значения по недостатку и по избытку с точностью до 0,01 для чисел: а) √5; б) 2+√5; в) 7/22.
Начнем рассмотрение по порядку: число из примера а) √5 = 2,236… из чего следует, что приближенным по недостатку с точностью до 0,01 будет число 2,23; а приближенным по избытку будет значение 2,24 с точностью до одной сотой.
В случае б) для начала рассчитываем значение самого числа: 2+√5, которое представляет собой сумму чисел 2,000… и 2,236…, то есть 4,236. Из чего следует, что4,23 — это приближение по недостатку с точностью до одной сотой; а4,24 - по избытку с той же точностью
Решение последнего из приведенных заданий вы можете увидеть, ознакомившись более детально с предложенным видео.
Следует отметить, что приближенные значения действительных чисел характеризуются погрешностью относительно исходного числа. Например, исходное число – некоторое число х, а число а – его приближенное значение. То абсолютная погрешность будет составлять их разность. Например, погрешность приближенного равенстваp»3,141 или p»3,141 будет записываться как |p-3,141| или, соответственно, как |p-3,142|.
Исходя из практической точки зрения, существует четко сформулированное правило округления действительных чисел, записанных в виде бесконечных десятичных дробей. Это правило звучит следующим образом: если первая отбрасываемая цифра меньше пяти, то нужно брать приближение по недостатку; а если первая отбрасываемая цифра больше или равна пяти, то нужно брать приближение по избытку.
Рассмотрим несколько примеров для подтверждения озвученного правила. Более подробно они будут представлены в предлагаемом вашему вниманию видео.
Итак, первый пример, это число p= 3,141592... . С точностью до 1 тысячной имеем p»3,142, так как последняя отбрасываемая цифра здесь - это пять, а мы помним, если оно является 5 или больше, то приближение происходит в сторону избытка. То же самое число в случае точности одной десятитысячной, то p»3,1416, так как отбрасываемая цифра – это девять. А в случае точности одной сотой части - p»3,14, из-за того, что единица является последним отбрасываемым числом.

С остальными примерами вас познакомит представленный видеоматериал на указанную тему.
Подведем итог, если число а – это приближенное значение числа х, и |x-a| ≤ h, то говорят, что погрешность приближения не превосходит h.
С практической точки зрения использование приближенных значений действительных чисел является более рациональным ввиду сложности использования бесконечных десятичных дробей.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9091 |
| Номер материала | 574 |