
Урок "Решение квадратных неравенств" Часть 2

Краткое описание документа:
Представляем вашему вниманию еще один из наших видео уроков по математике. Сегодня мы продолжим тему решения квадратных неравенств, с которыми вы начали знакомиться в предыдущем видео.

Не лишним будет напомнить, что квадратное неравенство имеет следующий вид: ах2+bх+с<0, при условии, что а не равняется нулю. Также следует отметить, что знак неравенства может быть представлен не только тем, который обозначен в примере, но и любым другим.
В данном видео мы рассмотрим вторую теорему, характеризующую квадратные неравенства. Она звучит следующим образом: если квадратный трехчлен ах2+bх+с не имеет корней (то есть его дискриминант D является отрицательным числом) и если при этом значение а находится в пределах меньше нуля, то при всех значениях х будет выполняться равенство ах2+bх+с<0.
То есть получается, что если дискриминант имеет отрицательное значение, и коэффициент а также является отрицательным числом, то указанное в теореме неравенство выполняется при всех значениях переменной, а квадратное уравнение с противоположным знаком неравенства не будет иметь решений в текущих условиях.
В подтверждение каждой теоремы проводят ее доказательство. В представленном видео вы можете более детально с ним ознакомиться.
График для функции вида у = ах2+bх+с представлен в виде параболы, поскольку коэффициент а отрицательный, то ветви ее направлены вниз, при этом, нет точек пересечения с осью абсцисс, так как корней у данного квадратного трехчлена нет по условию. Само изображение графика в системе координат и его более детальное описание вы можете увидеть, обратившись к предложенному видео.
Для большей наглядности, а также для представления возможности использования этой теоремы в действии, видео предлагает несколько примеров с разным уровнем сложности. Рассмотрим их кратно, более полные объяснения представлены в нашем видео уроке.
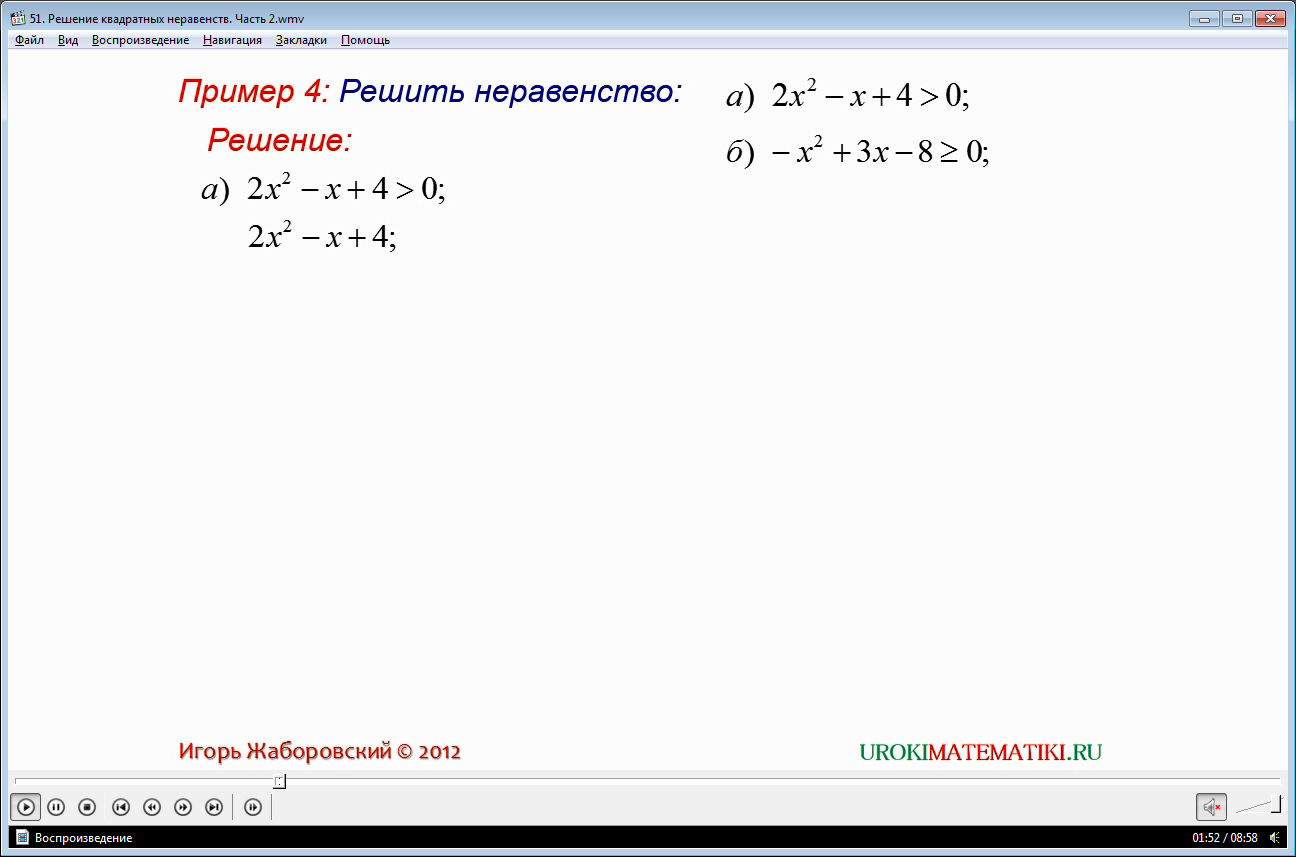
Рассмотрим первый из примеров. Нам предлагают решить неравенства:
а) 2х2-х+4 > 0; б) -х2+ 3х - 8 ³ 0.
Решение неравенства «а» начинаем с расчета дискриминанта квадратного трехчлена 2х2-х+4. Подставляя значения коэффициентов а, b и c получаем, что дискриминант равняется –31, что меньше нуля.
Поэтому решением заданного неравенства служит вся прямая от бесконечности со знаком минус и до бесконечности со знаком плюс.
Для решения неравенства «б» также, для начала, находимо значение дискриминанта квадратного трехчлена - х2+3х–8, которое равняется -23, то есть также имеет значение меньше нуля. Старший коэффициент трехчлена отрицателен. И, если исходить из второй теоремы, то при всех значениях переменной х указанное неравенство выполняется. Из этого следует, что неравенство -х2+3х-8 ³ 0 не выполняется ни при каком из значении х, то есть не имеет решений.
В итоге получается, что для неравенства «а» значении аргумента может быть любым действительным числом от бесконечности со знаком минус и до бесконечности со знаком плюс. В случае «б» неравенство не имеет решения, то есть ни одно из значений х не сможет удовлетворить заданные условия.
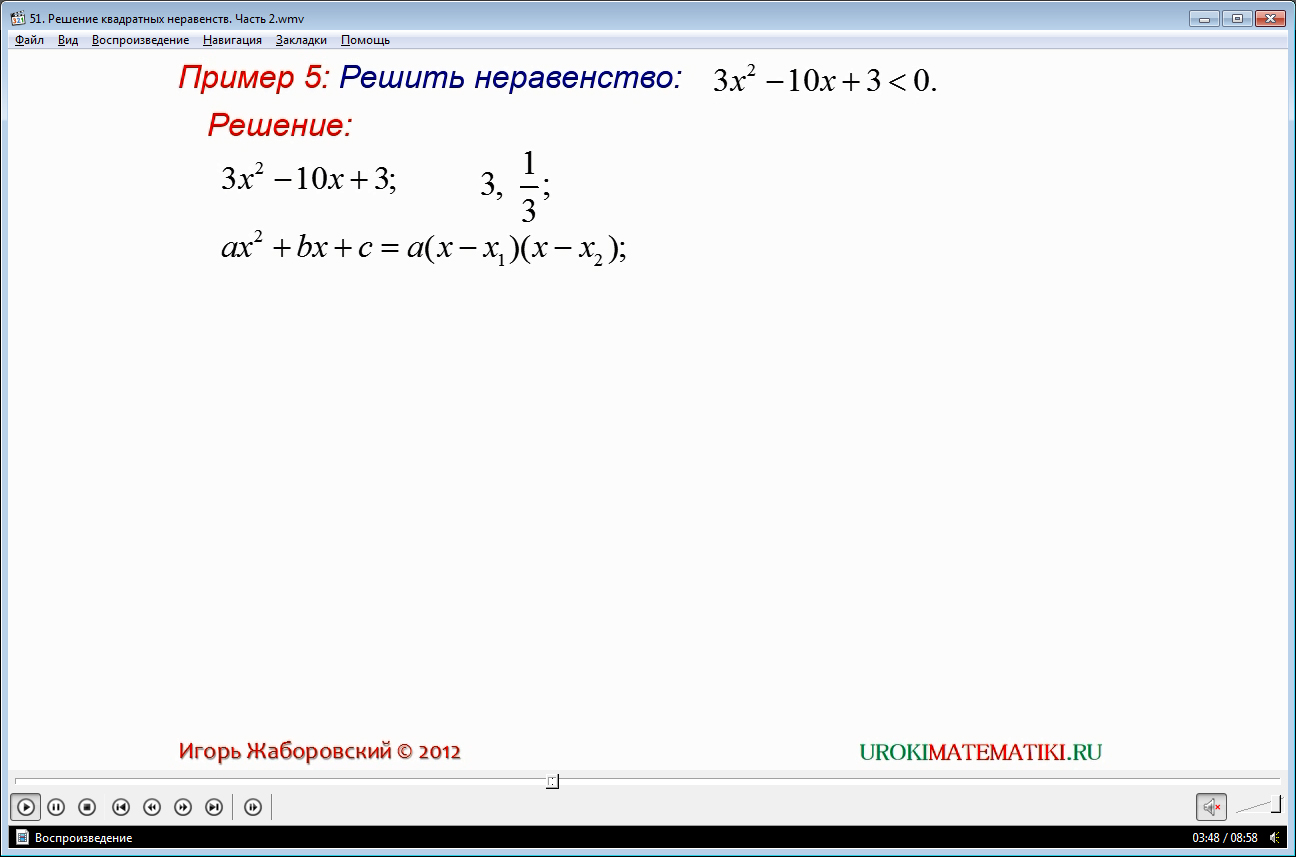
Следующий пример, представленный в видео, познакомит с еще одним способом решения квадратных неравенств - способом рассуждений.
Для этого предлагается решить следующее неравенство: 3х2-10х+3 < 0.
Для начала раскладывают предложенный квадратный трехчлен на множители, его корнями есть числа 3 и 1/3. Далее видео предлагает отметить эти значения на числовой прямой. В итоге, у нас получилось три отрезка для значений переменной: от минус бесконечности до 1/3, от 1/3 до 3 и от 3 до плюс бесконечности. Путем рассуждений приходим к ответу, который и удовлетворит наше неравенство, который вы узнаете, просмотрев предложенное видео. Вы сможете ознакомиться с более детальным решением этого примера, а также с еще одним случаем применения, изученной на этом занятии, теоремы вы сможете ознакомиться, просмотрев видео урок до конца.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4738 |
| Номер материала | 573 |