
Урок "Применение производной для поиска наибольшего, наименьшего значения"

Краткое описание документа:
Видеоурок «Применение производной в определении наибольших, наименьших значений» просто и наглядно раскрывает данную тему урока. Представляя тему, пособие демонстрирует теоретические основы определения наибольшего, наименьшего значения функциональной зависимости, приложение данных знаний к решению не только математических, но и физических задач. Демонстрируется понятный механизм исследования функции, нахождения ее экстремальных, крайних значений. Видеоурок служит способом повышения эффективности обучения. Он может использоваться вместо объяснения учителя, освобождая его для усиления индивидуальной работы или служить наглядным пособием, сопровождая рассказ учителя.
Демонстрация начинается с представления темы видеоурока. На рисунке изображается график y=f(x), непрерывный на промежутке [a;b]. Указываются наибольшее, наименьшее значение представляемой функции. Чтобы сформировать глубокое понимание материала, демонстрируются особенности нахождения таких значений на различных графиках. На следующем рисунке отображается график, расположенный выше оси абсцисс, наименьшее значение которого представлено точкой минимума функции. Отмечается правило, что непрерывная функция на некотором промежутке имеет наибольшее и наименьшее значения на нем. Второе правило указывает на расположение наибольшего и наименьшего значений внутри отрезка или на его концах. Все три рисунка демонстрируют различное расположение наибольшего, наименьшего значений – внутри графика, на концах. Также отмечается правило, внутреннее расположение точек совпадает с экстремумом. Ниже правила отображается напоминание ученикам, что такое стационарные и критические точки.
Знания обобщаются в виде представленного ученикам алгоритма. В состав алгоритма входит всего тир шага: нахождение производной функциональной зависимости f′(x), поиск на [a;b] стационарных, критических точек, затем поиск значений функции в особых точках, на концах промежутка, выбор среди значений наибольшего, наименьшего.
Иллюстрация применения алгоритма выполняется на примере поиска наибольшего, наименьшего значений y=х3+3/x на промежутке [1/2;2]. Первым делом определяется производная у′=(х3+3/х)′=(3х4-3)/ х2. Находятся критические точки с нулевой производной: у′=0 в точках х1=1, х2=-1. Составляется таблица, в которой находится значение стационарных точек и расположенных на концах отрезка. Проанализировав содержание таблицы, можно подытожить, что наименьшее значение y=4 в х=1, также наибольшее значение достигается на конце промежутка - в точке х=2, равно у=9,5.
Также представляется теорема, регулирующая поиск на интервале наибольшего, наименьшего значения. Отмечается, что для непрерывной функции, имеющей единственную особую точку х=х0, если х0 максимум, то это наибольшее значение, а если х0 минимум, то это наименьшее значение. Рядом с теоремой на рисунках демонстрируется, как минимум, максимум функции становится ее наибольшим (наименьшим) значением.
Далее в примере 2 необходимо найти крайние значения функции y=2x3+3х2-36х на промежутке [-2;+∞). На первом шаге исследования определяется производная y′=(2x3+3х2-36х)′=6х2+6x-36. В точках х=-3 и х=2 производная нулевая. Промежутку принадлежит х=2. На координатной прямой отмечается данная точка, указывается знак производной с обеих сторон. Очевидно, что эта точка – минимум. На данном промежутке точка х=2 является единственной стационарной точкой, поэтому, согласно теореме, она - наименьшее значение. В данной точке умин.=-44.
Делается небольшой экскурс в историю математики. Демонстрируется портрет знаменитого математика, сделавшего большой вклад в науку. Отмечается выражение математика, который выделяет важность математических методов для решения прикладных задач и определения наибольшей выгоды при использовании различных средств.
Дается алгоритм решения задач по оптимизации процессов, в которых требуется отыскать крайнее значение функции. Начальным этапом решения задач является составление математической модели. Выделяется оптимизируемая величина, устанавливается независимая переменная с реальными границами ее изменения. Описывается функциональная зависимость у от х, то есть y=f(x) с областью определения Х. На следующем этапе решения выполняется работа с математической моделью. Находится наименьшее, наибольшее значение. Третий этап решения формирует ответ, следующий из условия.
В примере 3 необходимо отыскать такое сечение балки, чтобы она имела наибольшую прочность, при известном факте, что прочность балки прямо пропорциональна произведению ширины и квадрата высоты, а радиус бревна, из которого она изготавливается – R.
На первом этапе решения задачи определяется оптимизируемая величина – это прочность, так как необходимо, чтобы она была наибольшей. Принимается независимая переменная – за х принимается ширина балки, которая может меняться от 0 до 2R. На рисунке демонстрируется сечение бревна, отмечая его радиус и возможную форму сечения балки. Составляется функциональная зависимость, которая отображает особенность формирования сечения и зависимости от нее прочности балки: х2+h2=4R2, у/хh2=k, где коэффициент пропорциональности k. Отсюда получаем функцию у= kх(4R2-х2), где х[0;2R]. Определяется наибольшее значение у= 4kхR2-kх3. Для этого находим производную у′=4kR2-3kх2. При решении уравнения у′=0, (4kR2-3kх2)′=0, определяются его корни х1=2R/√3, х2=-2R/√3. Области определения принадлежит х1=2R/√3. Находим значения функции в особой точке и на концах промежутка f(0)=0, f(2R)=0, f(2R/√3)=16kR3/3√3. Очевидно, наибольшее значение f(2R/√3)=16kR3/3√3. На третьем этапе определяем оптимальное значение сечения балки. Так как оптимальное значение прочности в точке х=2R/√3, находим высоту балки h2=4R2-х2. Подставив значение х и преобразовав выражение, получим h=2R√2/√3. Отсюда h/х=√2. Искомое значение h/х=√2≈1,4.
Видеоурок «Применение производной в определении наибольших, наименьших значений» рекомендуется использовать на традиционных школьных уроках математики. Также пособие может быть полезным учителю, осуществляющему дистанционное обучение. Чтобы углубить понимание предмета учеником, пособие может быть рекомендовано ему для самостоятельной работы.
ТЕКСТОВАЯ РАСШИФРОВКА:
Часто для отыскания наибольшего и наименьшего значений функции используется производная.
Пусть функция y = f(x) непрерывна на отрезке [а, b] (от а до бэ)– несколько графиков таких функций представлено на рис. 1—3. Рассмотрим графики функций, и делаем следующие выводы.
1. Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего, и своего наименьшего значений.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
Здесь возможны варианты — некоторые из них представлены на рис. 1–3. На первом график наибольшее и наименьшее значения достигаются внутри отрезка [a; b]. На втром графике наименьшее значение достигается внутри отрезка, а наибольшее — в концевой точке при х=b. На третьем графике и наибольшее, и наименьшее значения достигаются в концевых точках отрезка [a; b].
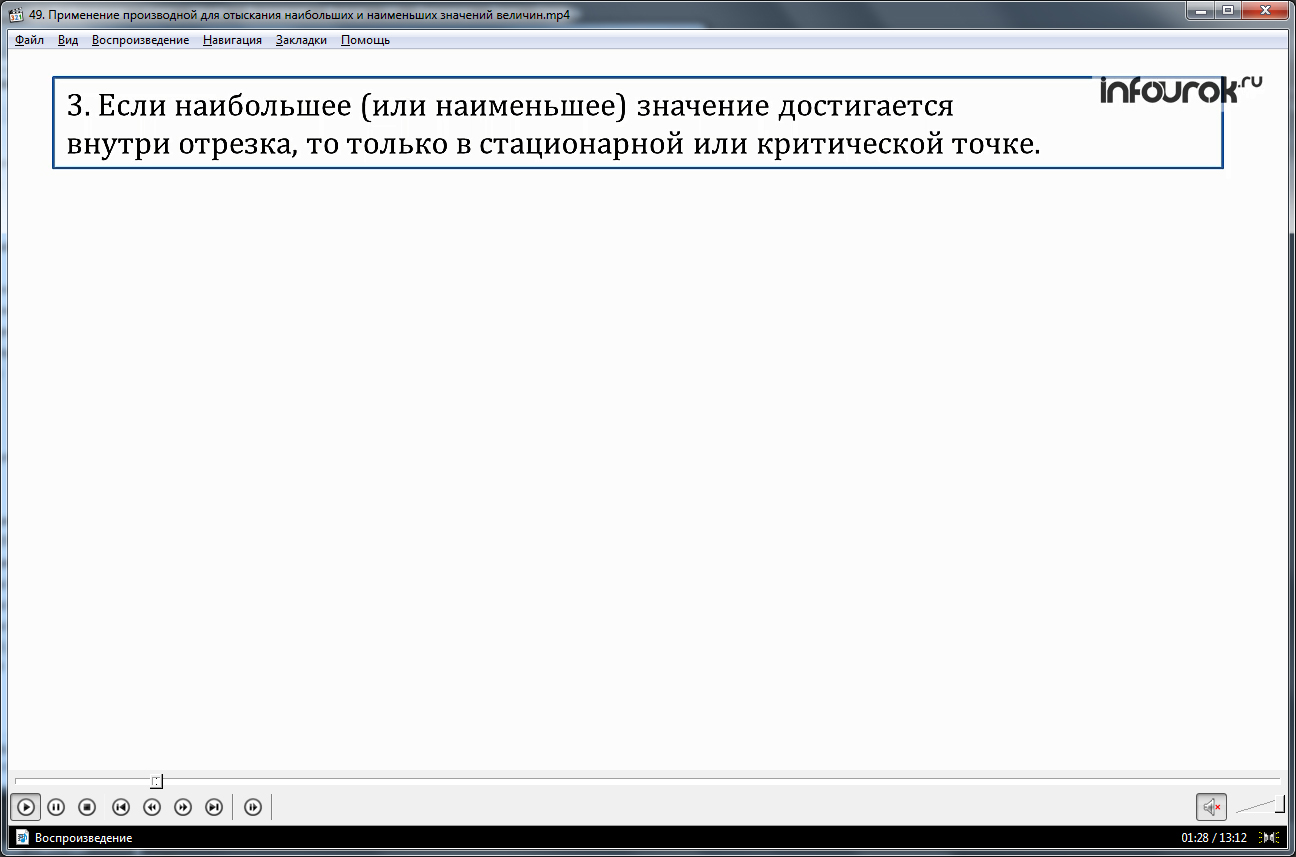
3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Напомним стационарные точки– это точки максимума или минмума, а критические точки – это точки в которых производная не существует.
Рассмотрим алгоритм отыскания наименьшего и наибольшего значений непрерывной функции на отрезке.
АЛГОРИТМ ОТЫСКАНИЯ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЙ НЕПРЕРЫВНОЙ ФУНКЦИИ у = f(x) НА ОТРЕЗКЕ [а, b]
1. Найти производную f'(x).
2. Найти стационарные и критические точки функции, лежащие внутри отрезка [а, b].
3. Вычислить значения функции y = f(x) в точках, отобранных на втором шаге, и в точках а и b; выбрать среди этих значений наименьшее (это и будет унаим.) и наибольшее (это и будет унаиб.).
Алгоритм, простой, для его иллюстрации достаточно приведем один пример.
Пример 1. Пример 3. Найти наибольшее и наименьшее значение функции
y = х3 + на отрезке .
Решение. Воспользуемся алгоритмом.
1) Имеем у'=3х2 – =. (игрек штрих равно три икс квадрат минус три, деленное на икс квадрат)
2) Производная существует при всех х, значит, критических точек у функции нет, а стационарные найдем из условия у'=0 (игрек штрих равно нулю). Имеем:
3x4 –3=0;
х1 = 1, х2 =–1.
Заданному отрезку принадлежит только одна стационарная точка х = 1. Значит, на третьем шаге алгоритма мы составим таблицу значений функции y= х3 + в стационарных точках и в крайних точка отрезка:
Таким образом, yнаим.=4 (нименьшее значение функции равное 4) достигается в точке х = 1;
унаиб.= (достигается в точке х = 2).
При решении многих задач часто приходиться находить наибольшее или наименьшее заначение функции не на отрезке, а на интервале, тогда бумем пользоватся следуюшей теоремой.
Теорема. Пусть функция y = f(x) непрерывна на промежутке X и имеет внутри него единственную стационарную или критическую точку х = х0. Тогда:
а) если х = х0 — точка максимума, то унаиб.= f(x0); Рис. 4
б) если х = х0 — точка минимума, то yнаим.= f(x0). Рис. 5.
На рис. 4 и 5 приведены соответствующие геометрические иллюстрации.
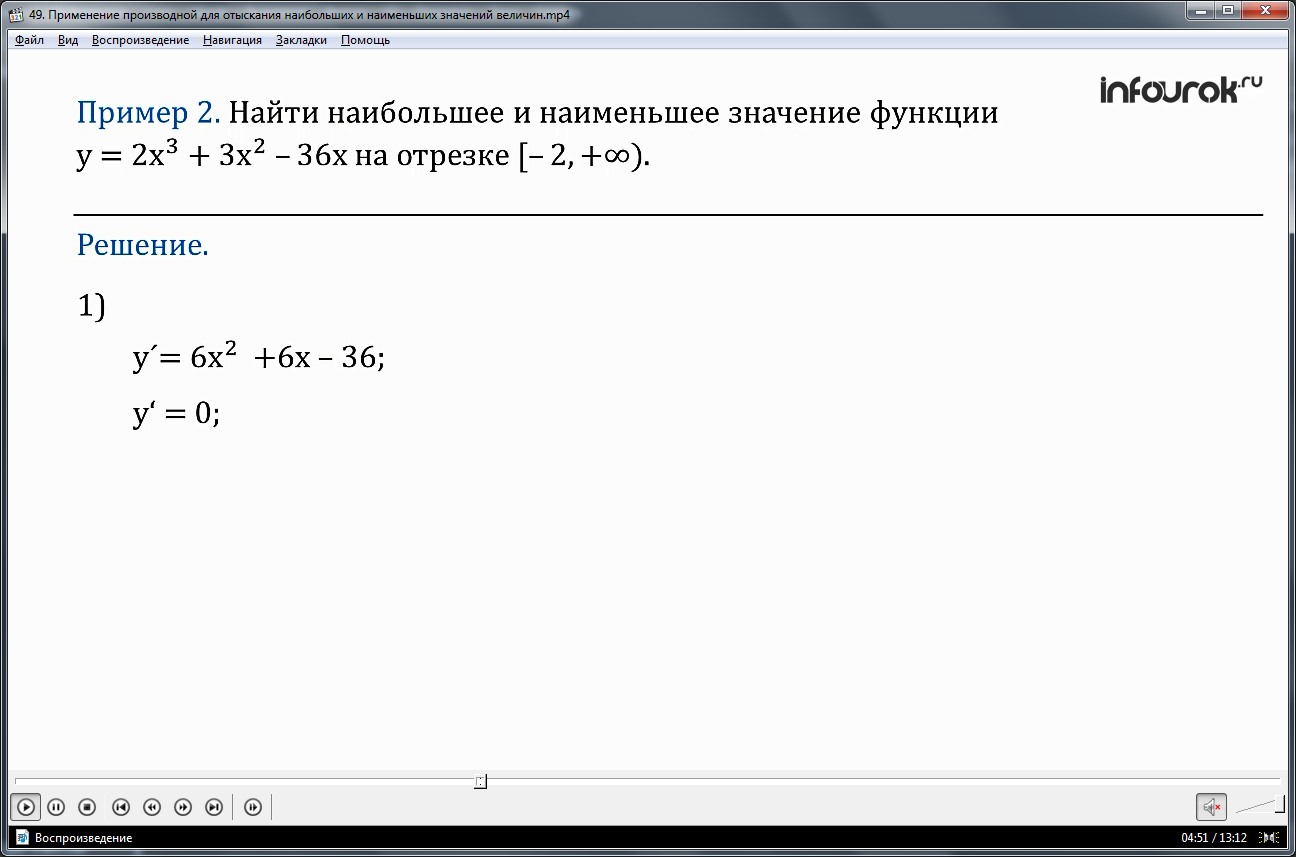
Пример 2. Найти наибольшее и наименьшее значение функции
y =2х3+3х2–36х на интервале [–2; +). (от минус двух включительно до плюс бесконечности)
Решение: y´= 6x2+6x–36.
Производная всюду существует, значит, критических точек у функции нет. Стационарные точки найдем из соотношения у'=0. Получаем: 6x2+6x–36 =0, откуда находим, что х = –3 или х = 2. Заданному лучу [–2, +) принадлежит одна из стационарных точек х=2. Изобразим луч на координатной прямой и отметим стационарную точку, найдем знаки производной в каждом из полученных промежутков.
При х < 2 имеем у'<0, а при х > 2 имеем у'>0. Значит, х= 2 точка минимума функции, причем ymin= f(2)=2∙23+3∙22–36∙2 =–44.
Поскольку х = 2 – единственная точка экстремума функции на заданном промежутке, причем точка минимума, то, по изученной выше теореме,
yнаим.= ymin= f(2)= –44.
Ответ: yнаим.= –44.
2. Задачи иа отыскание наибольших и наименьших значений величин
Как говорил российский математик XIX в. П.Л. Чебышев «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды».
Ведь наука должна помогать нам развиваться, облегчить труд, повысить производительность, снизить расходы и многое другое. И такие задачи существуют, они называются — задачи на оптимизацию (от латинского слова optimum — «наилучший»).
В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависитют другой, причем надо найти такое значение второй величины, при котором первая принимает свое наименьшее или наибольшее (наилучшее в данных условиях) значение.
Задачи на оптимизацию решают по плану состоящего из трех этапов математического моделирования:
1) составление математической модели;
2) работа с моделью;
3) ответ на вопрос задачи.
Рассмотрим рекомендации по реализации плана.
Первый этап. Составление математической модели.
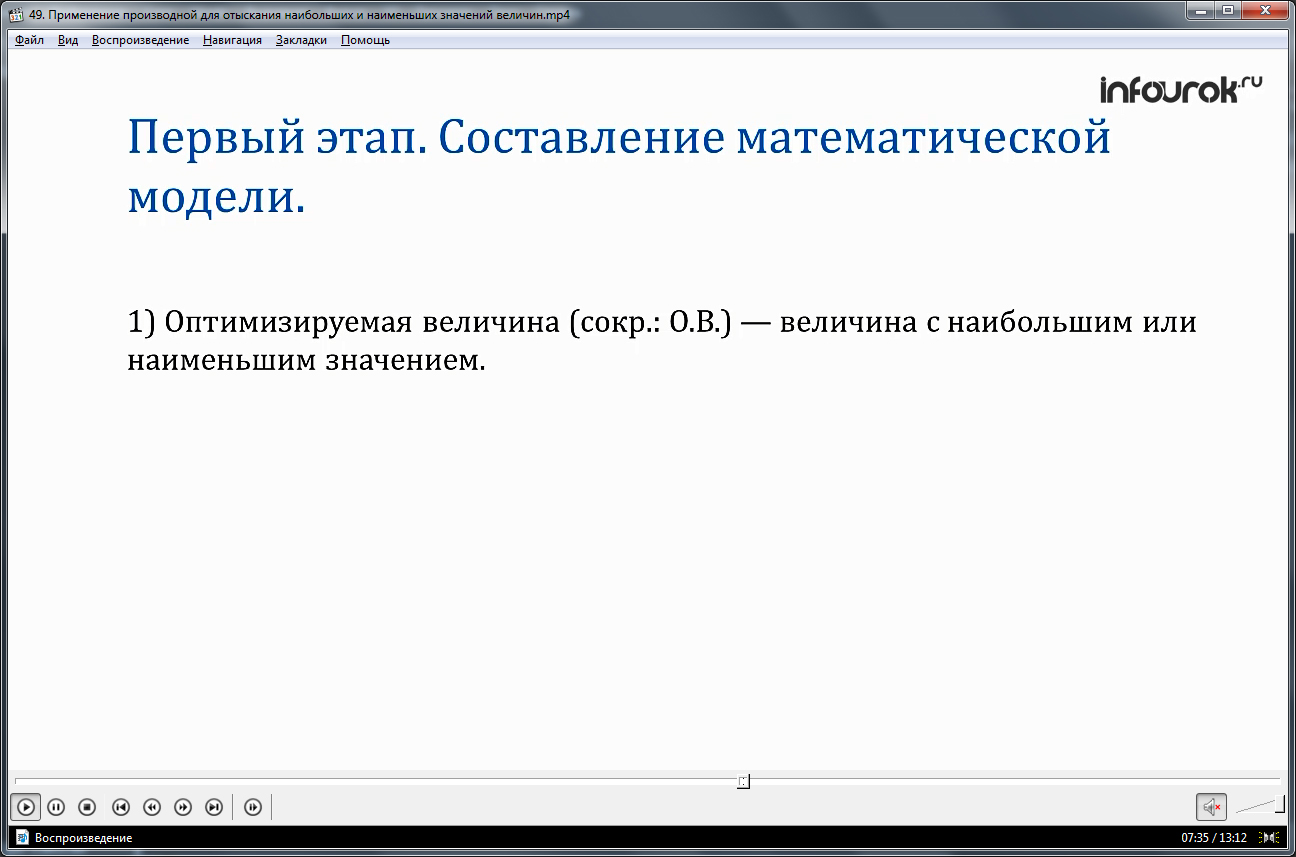
1) Проанализировав условия задачи, выделите оптимизируемую величину (сокращенно: О.В.), т.е. величину, о наибольшем или наименьшем значении которой идет речь. Обозначьте ее буквой у (или S, V, R, t — в зависимости от фабулы).
2) Другую неизвестную величину в задаче выразите через О.В., примите за независимую переменную (сокращенно: Н.П.), обозначьте ее буквой х. Установите реальные границы изменения Н.П. (в соответствии с условиями задачи).
3) Исходя из условий задачи, выразите у через х. Математическая модель задачи представляет собой функцию у = f(x) с областью определения X, которой является найденная граница задачи.
Второй этап. Работа с составленной моделью.
На этом этапе для функции у = f(x), xX найдите yнаим. или унаиб. в зависимости от того, что требуется в условии задачи.
Третий этап. Ответ на вопрос задачи.
Ответ получают в из условия задачи.
Рассмотрим одну из задач, которую предлагает нам автор учебника.
Пример 3 . Прочность балки прямоугольного сечения пропорциональна произведению ее ширины на квадрат высоты. Какое сечение должна иметь балка, вытесанная из цилиндрического бревна радиуса R, чтобы ее прочность была наибольшей?
Решение. Первый этап. Составление математической модели.
1) Оптимизируемая величина (О.В.) — прочность балки, поскольку в задаче требуется выяснить, когда прочность балки будет наибольшей. Обозначим её привычной нам буквой у.
2) Прочность зависит от ширины и высоты прямоугольника, служащего осевым сечением балки. Пусть независимой переменной будет ширина балки, обозначим ее буквой х. Так как осевое сечение прямоугольник, вписанный в окружность радиуса R (смотри рисунок 6), то 0<х<2R (при х= 0 и при x=2R прямоугольник обращается в отрезок, равный диаметру окружности) — это и есть реальные границы изменения независимой переменной. То есть область определения нашей математической модели (функции).
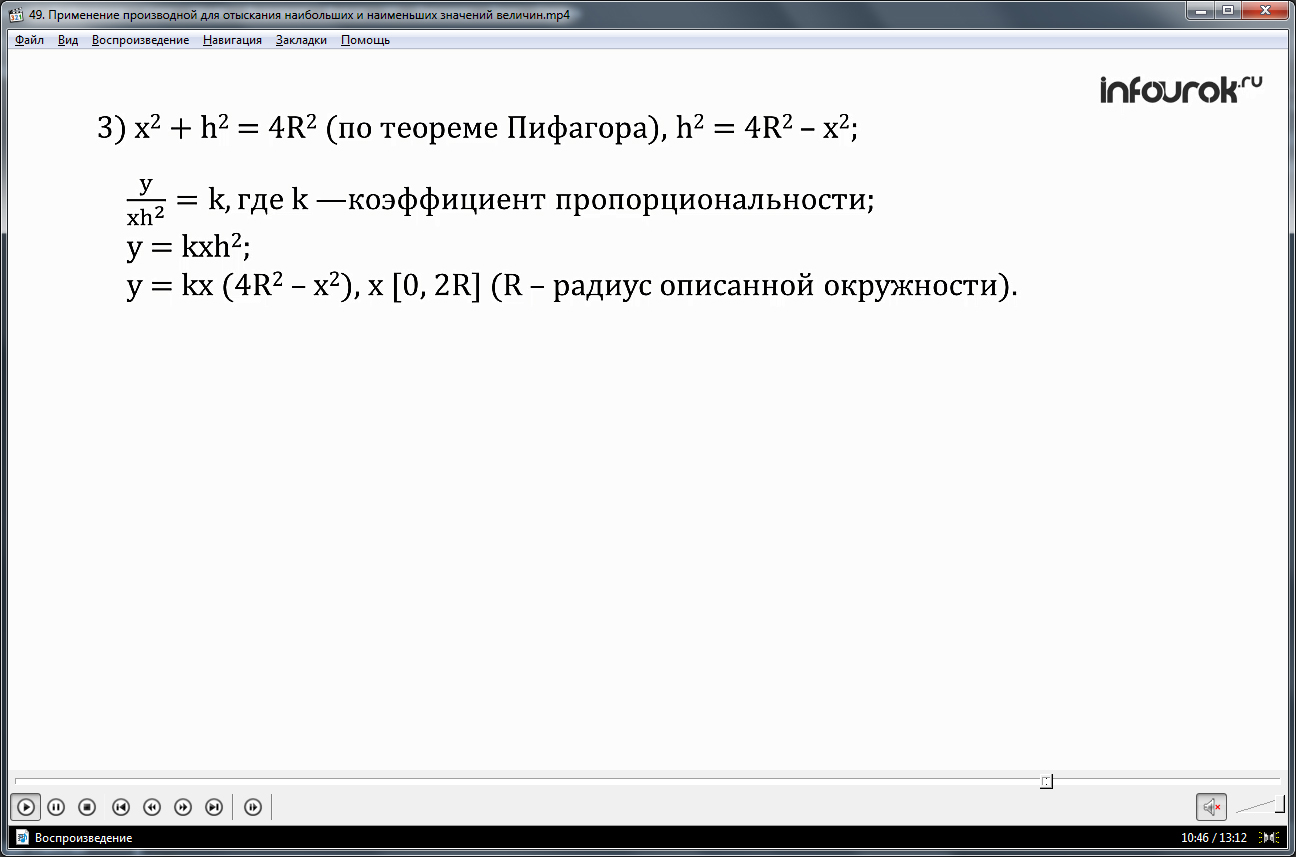
3) по теореме Пифагора, связываем высоту прямоугольника с шириной соотношением х2 + h2 =4R2 (икс в квадрате плюс аш в квадрате равно четыре эр в квадрате). Получаем, h2 =4R2 – х2.
По условию задачи прочность балки у пропорциональна произведению xh2. Так как величины пропорциональны, то их отношение ( ) равно некоторому числу k, которое называется коэффициентом
пропорциональности, т.е. получаем у = kxh2 (где коэффициент k — некоторое положительное число).
у=kx(4R2 – х2), где х[0, 2R]. (R – радиус описанной окружности)
Математическая модель задачи составлена.
Второй этап. Работа с составленной моделью.
На этом этапе для функции y=kx(4R2 –х2), x [0, 2R] надо найти унаиб.. (наибольшее значение функции)
Имеем:
раскрываем собки, получаем функцию y=4kR2x–kx3;
находим её производную (игрек штрих): y'=4kR2–3kx2.
Приравняв производную нулю, и решив квадратное уравнение относительно икс, получим два противоположных корня:
4kR2 –3kх2 =0;
x1=, x2= –.
Заданному отрезку [0, 2R] принадлежит лишь точка x = x1.
Далее вычислим значения функции y=kR2x–kx3 в точке x1 и на концах отрезка, т.е. в точках 0 и 2R.
Имеем:f(0) = 0, f(2R) = 0, f= >0. Значит, унаиб.= f.
Третий этап. Ответ на вопрос задачи.
В задаче необходимо найти сечение, которое должна иметь балка наибольшей прочности. Мы выяснили, что ширина х прямоугольника, служащего осевым сечением наиболее прочной балки, равна . Найдем высоту:
h2 =4R2 – х2, т.е. h2 =4R2 – =. h = .
Вычислим отношение, то есть коэффициент k для нашей математической модели, и зная его, мы при заданном радиусе сможем найти ширину и высоту балки: ,
Ответ: Сечением балки должен служить прямоугольник, у которого отношение высоты к ширине равно . (корню из двух или приблизительно 1,4).
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7329 |
| Номер материала | 872 |