
Урок "Применение производной в исследовании функций на максимум и минимум"

Краткое описание документа:
Видеоурок «Применение производной для исследования функций на экстремумы» предназначен для обеспечения наглядности при объяснении нового материала по данной теме. В ходе демонстрации раскрываются теоретические основы исследования функции на экстремум, ученикам представляются важные теоремы, рассматриваются примеры применения знаний об исследовании функции при решении задач. С помощью видеоурока учителю легче сформировать понятие учеников о точках экстремума и их нахождении при исследовании функции. Данный материал может применяться вместо объяснения учителя новой темы, а также сопровождать объяснение учителя, представляя наглядный материал.
Демонстрация начинается с представления темы урока. На экране изображается график функции y=f(x). На графике видно, что в точке х=-1 не существует касательной к графику, а в х=0 касательная является параллельной оси Х. Далее демонстрируется определение минимума функции. В нем указано, что минимумом функции y=f(x) является х=х0, для которой существует некоторая окрестность, где для всех точек окрестности справедливо f(x)> f(x0). С помощью рисунка разъясняется, что существует окрестность х=0 – к примеру, (-0,5;0,5), в которой все значения окрестности удовлетворяют условию f(x)> f(0). Делается замечание, что минимум функции не является ее наименьшим значением, так как говорится о наименьшем значении, когда рассматривается вся область определения. Поэтому часто унаим.≠умин.
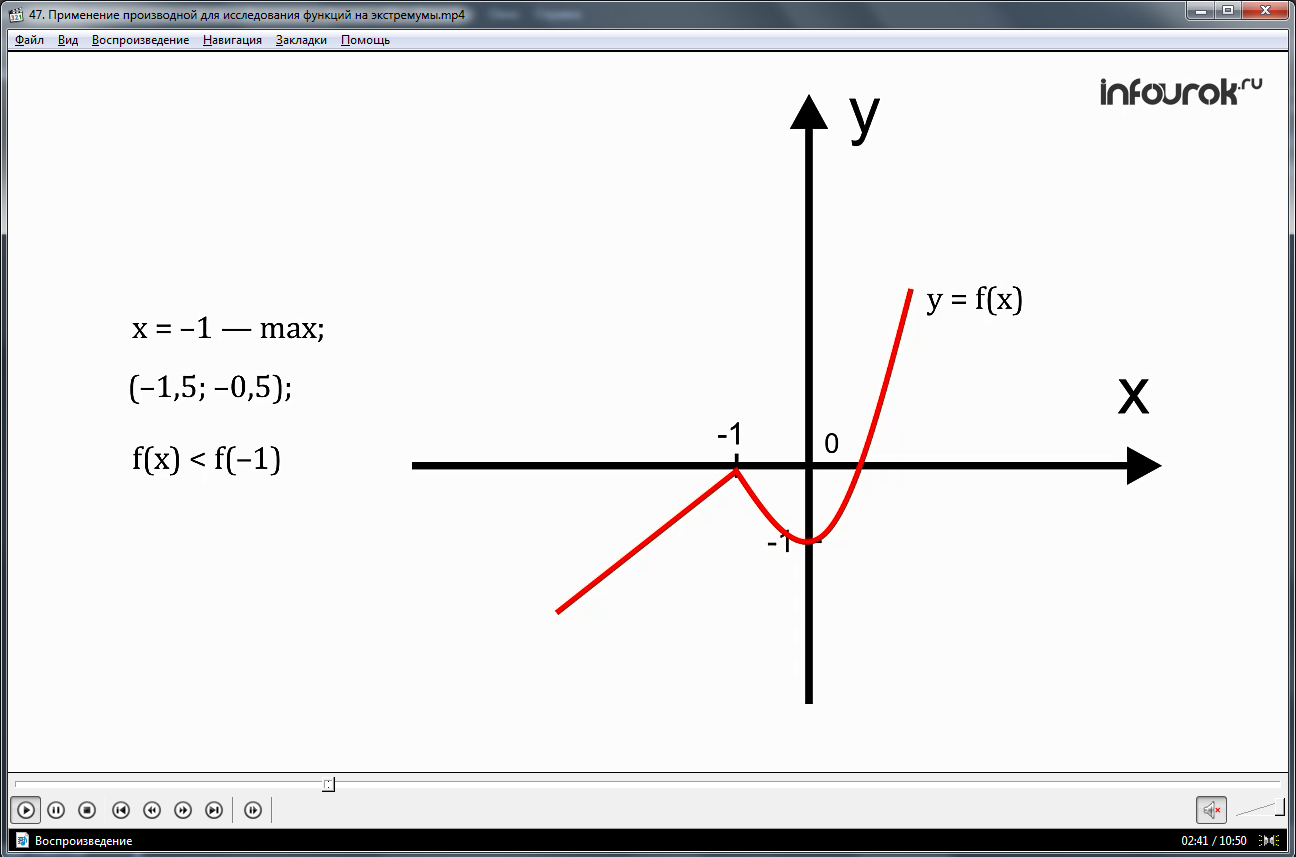
Представляется второе определение, где дается понятие о максимуме функции. Указана справедливость неравенства для окрестности максимальной точки f(x)<f(x0). На примере изображенного в начале видео графика функции y=f(x) разъясняется понятие максимума функции. На данном рисунке это точка х=-1, для окрестности которой, например, (-1,5;-0,5) верно f(x)<f(-1). Также отмечается различие понятий наибольшего значения функции и максимального. Понятие максимального значения функции расширено на всю область определения, в то время как минимальное значение отмечается на некоторой окрестности.
Далее представляется теорема, в которой раскрывается связь производной функции и экстремума. Отмечается, что если в данной точке функции есть экстремум, то производная в ней не существует или равна нулю. Очевидно, что при исследовании функции необходимо отыскать некие особые точки. Вводится понятие стационарных и критических точек. Стационарные точки определяются как точки, принадлежащие области определения функции, с производной, равной нулю. Критическими точками называют точки области определения, где функция непрерывна, однако производная не существует.
Рассматривается пример, в котором необходимо построить график функции у=-х2+4х-1. Зная особенности графика квадратичной функции, можно сразу сказать, что графиком данной зависимости является парабола с ветвями, направленными вниз, так как старший коэффициент функции отрицательный. Точкой максимума функции будет вершина этой параболы. Касательная к вершине параллельна оси Х, поэтому в вершине выполняется условие у΄=0. Находим производную функции у΄=(-х2+4х-1)΄=-2х+4. Решив уравнение -2х+4=0, получим х=2. В точке х=2 значение функции у=3. Найденная точка (2;3) и есть вершина параболы. Для построения параболы выбирается еще две симметричные точки – например (0;-1) и (4;0). Теперь изобразить график данной функции просто.
Далее представляется теорема 2, в которой указаны достаточные условия экстремума. В теореме указано, что для непрерывной на промежутке Х функции y=f(x), которая имеет в этом промежутке критическую точку х=х0, верно:
- при существовании около критической точки окрестности, где х<х0, f΄(x)<0, а для х>х0 f΄(x) >0, то точка - минимум функции;
- при существовании около критической точки окрестности, где х<х0, f΄(x) >0, а для х>х0 f΄(x) <0, то данная точка есть максимумом функции;
- при существовании около критической точки окрестности, где при переходе через данную точку знак не меняется, то экстремума здесь нет.
В примере 2 необходимо найти экстремумы и начертить график функции у=3х4-16x3+24х2-11,. Сначала определяется производная f΄(x)=( 3х4-16x3+24х2-11)΄. После преобразования производная принимает вид f΄(x)=12х(х-2)2. Решения уравнения - х=0 и х=2. Данные стационарные точки отмечаются на числовой прямой. Также на прямой отмечается, какой является функция на каждом из образованных промежутков – возрастающей или убывающей. Очевидно, что на промежутке (-∞;0) функция убывающая, так как производная принимает отрицательные значения, а на (0;2) и (2;+∞) производная положительна, функция возрастает. В х=0 функция изменяет направление с убывающей на возрастающую, эта точка - минимум, в х=2 не меняется знак производной, поэтому экстремума в ней нет. Находим в минимальной точке f(0)=-11. Соответственно, умин.=-11.
Для построения графика необходимо знать стационарные, критические точки. Определяем точки пересечения функции с координатными осями – это (-1;0), (1;0). Учитываем, что минимум функции - найденная (-11;0). А также стационарная точка (2;5), где касательная параллельна Х - точка перегиба. Найдя еще несколько координат точек, строится график функции.
Обобщая изученное, строится алгоритм исследования произвольной непрерывной функции y=f(x). В алгоритме присутствует 4 шага:
- поиск производной f΄(x);
- нахождение критических, стационарных точек;
- построение особых точек на координатной прямой - критических и стационарных, указание знака производной на образовавшихся промежутках;
- вывод о монотонности, экстремальных точках функции.
Отдельно выводится замечание о необходимости отметки на координатной прямой точек, которые обращают в нуль знаменатель вида p(x)/q(x). При этом указывается, что данные точки не экстремальные.
В примере 3 необходимо исследовать функцию у=(х2-3)/(х2+1). Функция исследуется согласно алгоритму. Сначала находится производная f΄(x)=((х2-3)/(х2+1))′. Воспользовавшись правилом нахождения производной частного, находим производную f΄(x)=8х/(х2+1)2. На координатной прямой указываем точку, где производная равна нулю - х=0. Далее расставляем знаки производной на сформированных промежутках. Очевидно, на промежутке (-∞;0] функция убывает, а возрастающая она на [0;+∞). Судя по свойствам графика, точка х=0 - это минимум функции, где умин.=-3.
Видеоурок «Применение производной в исследовании функций на экстремумы» рекомендуется использовать на традиционном уроке математики для повышения его эффективности. Также пособие может применяться учителем, осуществляющим дистанционное обучение, для более наглядного представления материала по теме. Ученикам, недостаточно хорошо усвоившим материал, пособие рекомендуется для самостоятельного рассмотрения.
ТЕКСТОВАЯ РАСШИФРОВКА:
2. Точки экстремума функции и их отыскание
Рассмотрим график функции, изображенный на рисунке 1. Данная функция не имеет касательной в точке х = –1, а в точке х = 0, она совпадает с осью у (т.е. перпендикулярна оси х).
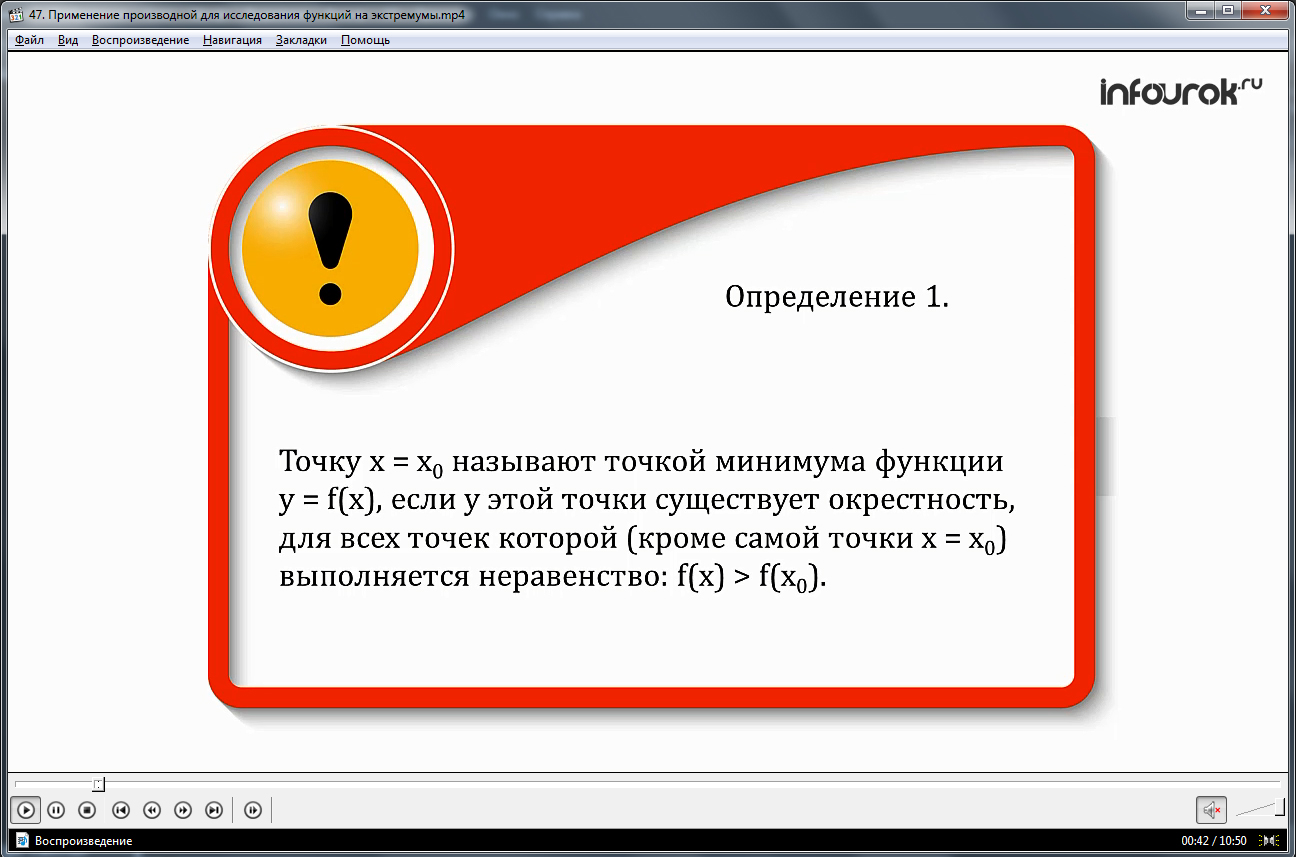
Определение 1. Точку х =х0 называют точкой минимума функции у = f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х =х0) выполняется неравенство:
f(x)>f(x0). (эф от икс больше эф от икс нулевого)
То есть, функция, график которой показан на рис. 1, имеет точку минимума х=0. Так как у данной точки существует окрестность, например, или (–0,5; 0,5), для всех точек которой, кроме точки х= 0, выполняется неравенство f(x) > f(0). (эф от икс больше эф от нуля)
Значение функции в точке минимума обозначают ymin. (игрек минимум)
Замечание. Но данное значение не является наименьшим значением функции, так как наименьшее значение рассматривает на всех области определения, то есть ymin часто отличается от yнаим. (игрек наименьшего)
Например, функция график которой изображен на рис. 1, не имеет наименьшего значения, но ymin(минимальное значение) существует.
Определение 2. Точку х = х0 называют точкой максимума функции у=f(x), если у этой точки существует окрестность, для всех точек которой, кроме самой точки х = х0, выполняется неравенство: f(x)<f(x0). (эф от икс меньше эф от икс нулевого)
Вернемся к рисунку 1, данная функция, имеет точку максимума х= –1. Так как у данной точки существует окрестность, например, (–1,5; –0,5), для всех точек которой, кроме точки х=–1, выполняется неравенство f(x)< f(–1).( эф от икс меньше эф от минус одного)
Значение функции в точке максимума обозначают ymax. (игрек максимальный)
Не путайте это значение с yнаиб.(игрек наибольший), т.е. с наибольшим значением функции во всей рассматриваемой области определения.
Мы можем утверждать, что наибольшего значения нет у рассматриваемой функции, aymax(максимальное значение ) существует.
Точки минимума и максимума функции объединяют общим термином – точки экстремума (от латинского слова extremum– «крайний»).
Теорема 1. Если функция у = f(x) имеет экстремум в точке х = х0, то в этой точке производная функции либо равна нулю, либо не существует.
Введем некоторые дополнительные обозначения: точки области определения функции, в которых производная функции равна нулю, называются стационарными, а точки области определения функции, в которых функция непрерывна, но производная функции не существует, — критическими.
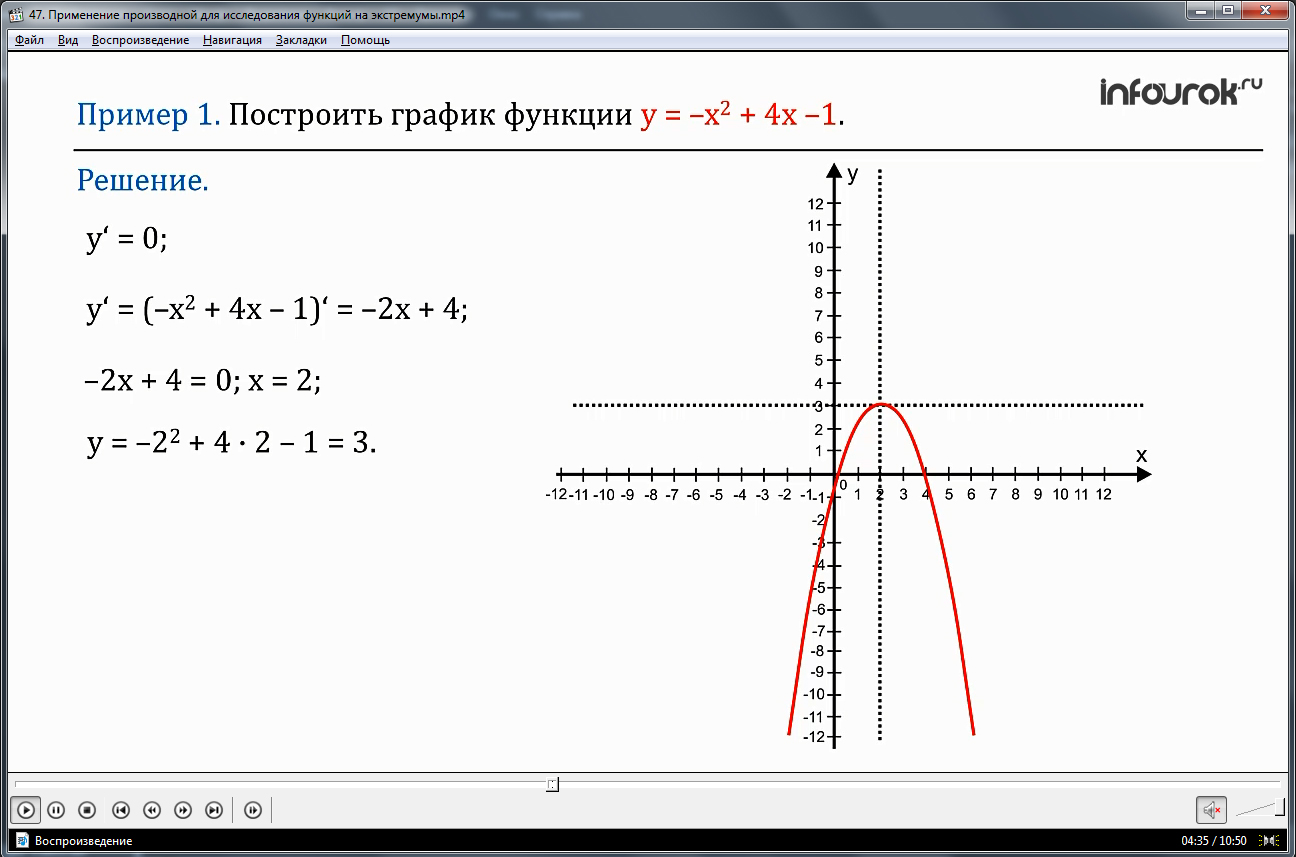
Пример 1. Построить график функции у = –х2 + 4х –1.
Решение. Вам известно, что графиком заданной квадратичной функции является парабола, причем ветви параболы направлены вниз, поскольку коэффициент при х2 отрицателен. Но в таком случае вершина параболы является точкой максимума функции, касательная к параболе в ее вершине параллельна оси х, значит, в вершине параболы должно выполняться условие у'=0. (игрек штрих равен нулю)
Имеем: у'=(–х2 + 4х –1)'= –2х+4.
Приравняв производную нулю, получим: –2х+4=0; x=2.
Подставив найденное значение х в уравнение параболы, получим:
у = –22 + 4·2 –1= 3. (игрек равен трем)
Итак, вершиной параболы служит точка (2; 3), а осью параболы – прямая х=2. В качестве контрольных точек удобно взять точку (0; –1) и
симметричную ей относительно оси параболы точку (4; –1). На рис. 2 по найденным трем точкам построена парабола — график заданной квадратичной функции.
Теорема 2 (достаточные условия экстремума). Пусть функция y=f(x) непрерывна на промежутке X и имеет внутри промежутка стационарную или критическую точку х = х0. Тогда:
а) если у этой точки существует такая окрестность, что в ней при х<х0 выполняется неравенство f´(х) < 0, а при х>х0 — неравенство f´(x)>0, то
х = х0 — точка минимума функции y=f(x);
б) если у этой точки существует такая окрестность, что в ней при х<х0 выполняется неравенство f ´(х)>0,а при х>х0 — неравенство f ´(x)<0, то
х = х0 — точка максимума функции y=f(х);
в) если у этой точки существует такая окрестность, что в ней и слева, и справа от точки х0 знаки производной одинаковы, то в точке х = х0 экстремума нет.
Пример 2. а) Найти точки экстремума функции у = 3х4–16х3+24х2–11;
б) построить график этой функции.
Решение, а) Найдем производную данной функции: f´(x) = 12х3–48х2+48х
и далее
f´(x) = 12x(х2–4х+4);
f´(x) = 12x(х–2)2;
Производная обращается в нуль в точках х = 0 и х = 2 – это две стационарные точки заданной функции. На рис. 3 схематически указаны знаки производной и поведение функции по промежуткам области определения: на промежутке (–, 0) производная отрицательна, значит функция убывает, на промежутках (0, 2) и (2, +) — положительна, функция возрастает. Точка, х = 0 — точка минимума функции, а х = 2 точкой экстремума не является.
В точке минимума х = 0 имеем f(0) = –11 (подставили значение х = 0 в
аналитическое задание функции), значит, уmin = –11.
б) Чтобы построить график функции, нужно знать особо важные точки
графика. К таковым относятся:
— найденная точка минимума (0; –1);
— стационарная точка х = 2; в этой точке f(x) = 3 ·24 –16· 23 +24∙22 –11=5;
— точки пересечения с осями координат; в данном примере это уже найденная точка (0; –11) — точка пересечения графика с осью у. И еще: можно догадаться, что f(1)=0, значит, найдена точка пересечения графика с осью х — это точка (1; 0).
Итак, мы имеем точку минимума (0; –11), точку пересечения графика с
осью х — точку (1; 0) и стационарную точку (2; 5). В этой точке касательная к графику функции горизонтальна, но это не точка экстремума, а точка перегиба.
График функции схематически изображен на рис. 4. Заметим, что есть еще
одна точка пересечения графика с осью абсцисс, но найти ее нам не удалось.
Изученное обобщим в виде алгоритма.
АЛГОРИТМ ИССЛЕДОВАНИЯ НЕПРЕРЫВНОЙ ФУНКЦИИ y = f(x) HA МОНОТОННОСТЬ И ЭКСТРЕМУМЫ
1. Найти производную f'(x).
2. Найти стационарные и критические точки.
3. Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4. Опираясь на теоремы, сделать выводы о монотонности функции и о ее точках экстремума.
Замечание: если заданная функция имеет вид у = (игрек равен пэ от икс, деленное на ку от икс), то на числовой прямой необходимо отметить точки, в которых знаменатель q(x) обращается в нуль, до определения знаков производной. Но, данные точки не являются точками экстремума.
Пример 6. Исследовать функцию у = на монотонность и экстремумы.
Решение. Заметим, что функция всюду непрерывна, так как знаменатель в любой точке х больше нуля. Воспользуемся указанным выше алгоритмом.
1) Найдем производную заданной функции:
f´(x)==.
(эф штрих от икс равно восемь икс, деленное на квадрат суммы икс в квадрате и единицы).
2) Производная обращается в нуль в точках х = 0 это стационарная точка. Производная существует при любом х, критических точек, и точек разрыва функции нет.
3) Отметим точку 0 на числовой прямой и расставим знаки производной на получившихся промежутках (рис. 5).
4) Делаем выводы: на луче(–, 0] функция убывает, на луче[0, +)функция возрастает.
Далее, х = 0 – точка минимума, причем ymin=–3 (игрек минимальный равен минус три) (подставили значение x = 0 в формулу у =).
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8429 |
| Номер материала | 870 |