
Урок "Применение производной в исследовании функций. Построение графика функции"

Краткое описание документа:
Видеоурок «Применение производной в исследовании функций на монотонность. Построение графиков функций» есть наглядным пособием для ведения школьного урока математики по данной теме. В ходе рассмотрения темы обобщаются изученные понятия, необходимые для исследования функции и построения ее графика. Учитель формирует умение ученика строить график функции. Это важное умение для решения многих математических и прикладных задач. С помощью видеоурока учитель имеет возможность повысить эффективность занятия, освобождая время на объяснение для усиления индивидуальной работы с учащимися, или использует наглядность пособия для углубления понимания материала учениками.
Демонстрация начинается с представления темы урока. Отмечается, что построение графика на координатной плоскости выполняется по известным точкам, принадлежащим этому графику. На предыдущих занятиях уже изучены важные для построения точки. Также указано, что по сравнению с изученным ранее способом построения графика функции – строго по точкам, в курсе 10 класса поведение функции изучается более глубоко и применяется универсальный способ построения графика.
Первым выделяется правило построения функции, что непрерывна во всем множестве области определения. Отмечается, что для построения графика такой функции достаточно найти особые точки и промежутки монотонности. Затем достаточно отметить еще несколько точек, определяющих построение.
Во втором правиле рассматривается построение графика функции, что определена не на всей координатной прямой. Отмечается, что при построении графика такой функции вначале добавляется пункт отыскания области ее определения, нахождения точек разрыва.
Третье правило касается функций, обладающих свойством четности или нечетности. При определении такого свойства функции, можно построить одну ее ветвь, а затем начертить симметрично ей относительно оси или начала координат вторую часть графика.
В четвертом пункте отмечается особенность функции, стремящейся на бесконечности к некоторому числу lim f(x)=b при n→∞. Таким образом определяется горизонтальная асимптота y=b. Ее также необходимо строить.
Пятый пункт правила определяет построение вертикальной асимптоты графика, для которой характерно условие, что при стремлении х→а, значение функции стремится к бесконечности у→∞. Отдельно выделяется признак вертикальной асимптоты. В нем утверждается, что у функции вида f(x)=p(x)/q(x), знаменатель которой обращается в нуль точкой х=а, а числитель ненулевой, есть вертикальная асимптота х=а.
Рассматривается решение примеров, закрепляющих знания об исследовании функции. В примере 1 необходимо построить график функции у=8/(4+х2). Первым делом отмечается, что данная функция определяется по всей числовой прямой, то есть D(f)ϵ(-∞;+∞). Далее функция проверяется на четность. Для этого находится f(-x). После подстановки (-х) видно, функция преобразуется в исходную, так как знак аргумента не влияет на ее значение. Условие f(-x)=f(x) означает четность функции, то есть ее симметричность относительно оси ординат, поэтому достаточно построить одну ветвь для х>0, а затем отобразить ее. Чтобы определить горизонтальную асимптоту, находим предел lim f(x) при n→∞. Для нахождения lim 8/(4+х2) делим числитель и знаменатель на высшую степень аргумента. После преобразования и вычисления значения получаем lim 8/(4+х2)= 0 при n→∞. Значит, горизонтальная асимптота у=0. Для нахождения экстремумов и промежутков монотонности определяем производную и анализируем ее знак. Определяем у′=(8/(4+х2)′=-16х/(4+х2)2. Очевидно, производная существует для любого значения х, поэтому критические точки отсутствуют. Находим точки с производной, обращенной в нуль. У′=0 в точке х=0. Чтобы выяснить, есть ли в данной точке экстремум, отмечаем точку на координатной прямой, а также отмечаем знак производной функции на промежутках (-∞;0] и [0;+∞). На промежутке (-∞;0] функция возрастает, а на (-∞;0] – убывает. Поэтому можно сделать вывод о максимуме функции у=8/(4+х2) в точке х=0. В ней значение функции f(0)=2. Чтобы построить график, заполняем таблицу, в которой определяем координаты еще нескольких точек на разных промежутках. На следующем шаге строим график. На экране отображается координатная плоскость, где строится график функции. При этом в точке (0;2) располагается максимум функции, у=0 является асимптотой, к которой на бесконечности стремится график у=8/(4+х2). Построив часть графика в правой полуплоскости, симметрично ему строим график в левой полуплоскости, так как функция четная. Отмечается, что в математике данный график получил название «локон Аньези».
Во втором примере необходимо построить график функции у= (х2+1)/(х2-1). Сначала находим область определения. Обращаем внимание, что знаменатель будет равен нулю в случае х=1 и х=-1. Поэтому область определения разбивается на три промежутка (-∞;-1), (-1;1), (1;+∞). Вторым шагом исследования является исследование на четность. Путем анализа определяем, что f(-х)= f(х), что означает четность функции. Поэтому будет достаточно построить ветвь в положительной части прямой Х и симметрично отобразить ее на отрицательную часть. Определяется горизонтальная асимптота путем нахождения предела lim f(x) при n→∞. Преобразуем выражение под знаком предела, поделив числитель и знаменатель на высшую степень аргумента. После преобразования и вычисления значения получаем lim (х2+1)/(х2-1)=1 при n→∞. Горизонтальной асимптотой есть у=1. Для анализа монотонности и поиска экстремумов находим производную функции. Производная вычисляется, применив свойство производной частного у′=((х2+1)/(х2-1))′=-2х/(х2-1)2. Определяем, в каких точках у′=0. Производная нулевая в х=0. Чтобы определить экстремумы, указываем на числовой прямой все найденные особые точки х=-1, х=0, х=1, х=2. Анализируя знак производной, делаем вывод, что функция на промежутках (-∞;-1), (-1;0] возрастающая. Убывание функции наблюдается на промежутках [0;1) и (1;+∞). Соответственно, точка х=0 - максимум функции. Соответствующее значение у=-1. Дополнительно для построения графика составляется таблица, в которой отмечены особые точки и несколько других точек, нужных для построения. На координатной плоскости строится ветвь графика в положительной полуплоскости. Затем строится такая же ветвь в отрицательной полуплоскости симметрично относительно оси Y. На экране демонстрируется построенный график функции, учитывающий точку экстремума, горизонтальные и вертикальные асимптоты, симметричность.
Видеоурок «Применение производной в исследовании функций на монотонность. Построение графиков функций» рекомендуется использовать на традиционном уроке математики для повышения его эффективности. Также ученикам, недостаточно хорошо усвоившим предмет, материал рекомендуется для самостоятельного изучения. Учителю, проводящему дистанционное обучение, пособие поможет представить материал более понятным за счет наглядной демонстрации.
ТЕКСТОВАЯ РАСШИФРОВКА:
Графики функций можно построить по точкам. И поэтому часто необходимо уметь выделять — особо важные точки графика, определяющие его структуру.
К таким точкам графика функции у = f(x) (игрек равен эф от икс) относят:
— стационарные и критические точки;
— точки экстремума;
— точки пересечения графика с осями координат;
— точки разрыва функции.
В курсе математики нет четкой схемы исследования свойств функции и построения графика функции, но мы рассмотрим универсальную схему, позволяющую строить весьма сложные графики:
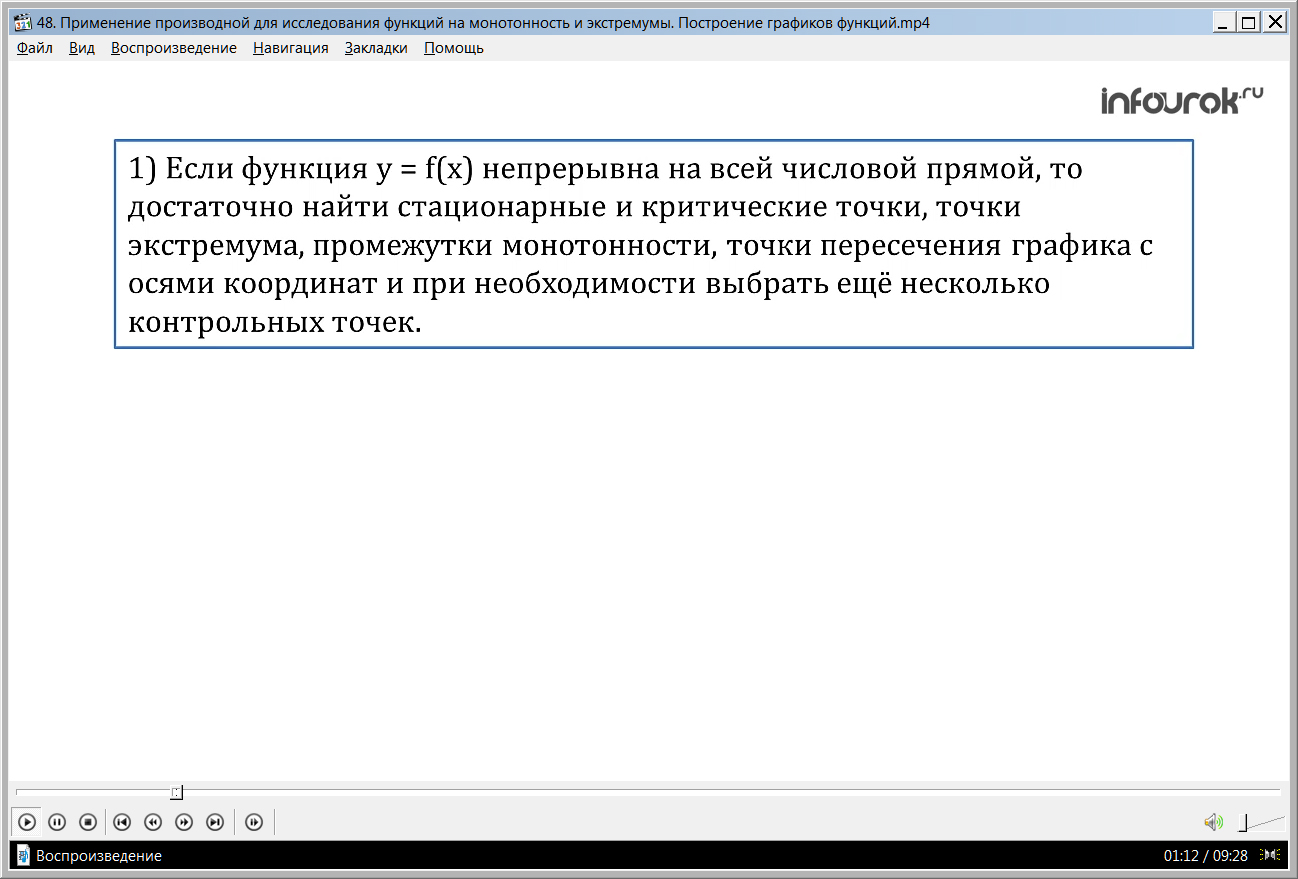
1) Если функция y = f(x) (игрек равен эф от икс) непрерывна на всей числовой прямой, то достаточно найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек.
2) Если функция у = f(x) (игрек равен эф от ихс) определена не на всей числовой прямой, то начинать следует с отыскания области определения функции и с указания ее точек разрыва.
3) Можно исследовать функцию на четность, так как графики четной или нечетной функции обладают симметрией (соответственно относительно оси ординат или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при х>0 (икс больше нуля), а затем достроить симметричную ветвь.
4) Если f(x) =b (предел функции при стремлении икс к бесконечности равен бэ), то, как известно, прямая у = b (игрек равен бэ) является горизонтальной асимптотой графика функции у = f(x) (игрек равен эф от икс). Асимптота является определенной границей графика, поэтому её необходимо строить.
5) Горизонтальная асимптота характеризуется условием: если х (икс стремится к бесконечности), то у b (игрек стремится к бэ). Но при условии: если х а (икс стремится к а), то у(игрек стремится к бесконечности), – прямая х = а (икс равен а) является вертикальной асимптотой графика функции у = f (x) (игрек равен эф от икс).
Самый распространенный признак существования вертикальной асимптоты заключается в следующем:
если f(x) = (эф от икс равно пэ от икс, деленное на ку от икс) и при х = а (икс равном а) знаменатель обращается в нуль, а числитель отличен от нуля, то х = а – вертикальная асимптота графика функции у = f(x) (игрек равен эф от икс).
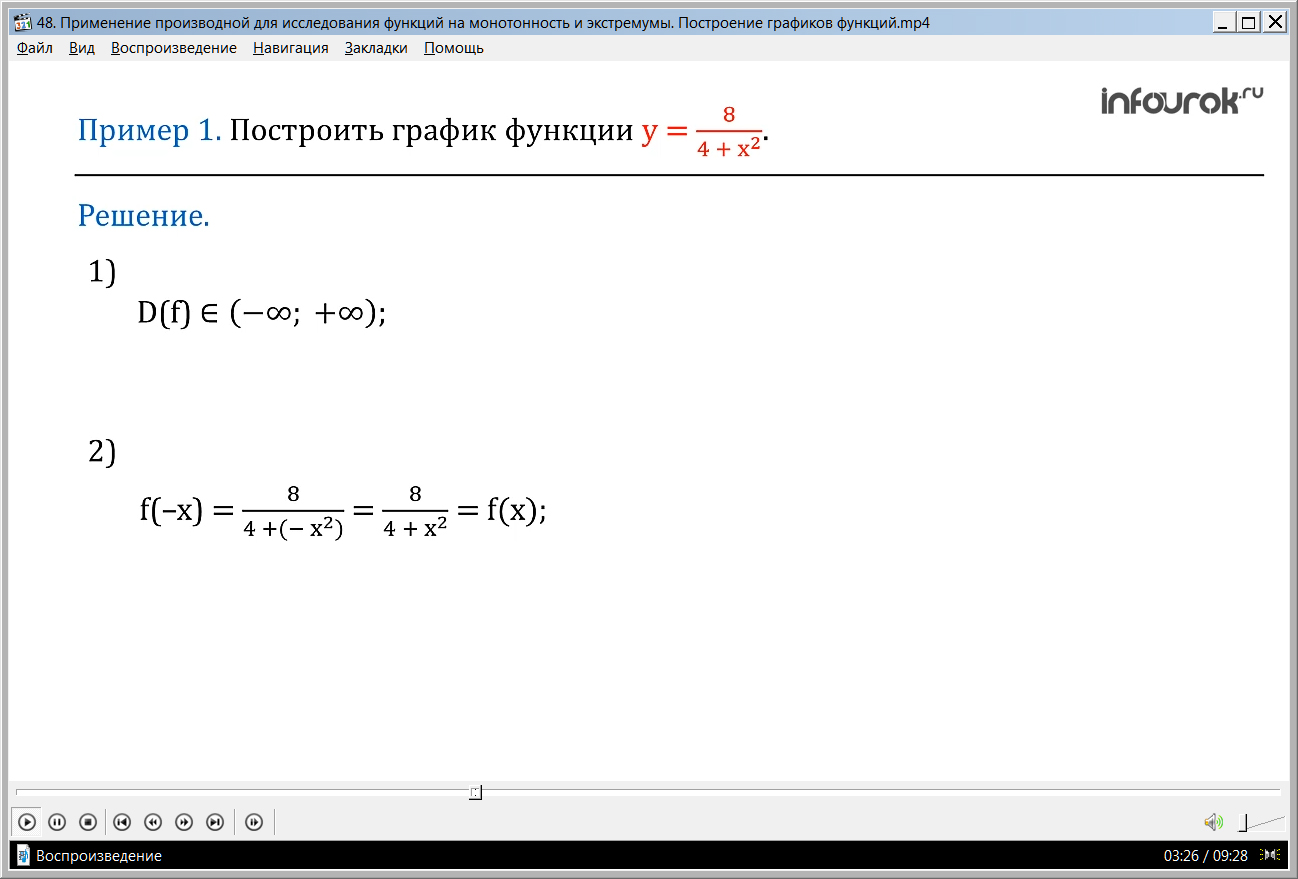
Пример 1. Построить график функции у = .(игрек равен восемь, деленное на четыре плюс икс в квадрате)
Решение. 1. Найдем область определения функции: D(f)=( –;+) (дэ от эф равно от минус бесконечности до плюс бесконечности), так как при любом икс знаменатель не равен нулю.
2. Исследуем функцию на четность: f(–x) = = = f(x) (эф от минус икс равен эф от икс).
Значит, заданная функция четная, ее график симметричен относительно
оси ординат, а потому можно изначально ограничиться построением
ветви графика при х0.
3. Найдем асимптоты. Вертикальной асимптоты нет. Для отыскания
горизонтальной асимптоты надо вычислить f(x) (предел функции при стремлении икс к бесконечности). Имеем:
(предел функции восемь, деленное на четыре плюс икс в квадрате при стремлении икс к бесконечности равен нулю)
Значит, у = 0 — горизонтальная асимптота графика функции.
4. Найдем стационарные и критические точки, точки экстремума и
промежутки монотонности функции. Имеем:
(игрек штрих равен минус шестнадцать икс, деленное на квадрат суммы четырех и икс в квадрате).
Производная всюду существует, значит, критических точек у функции нет.
Стационарные точки найдем из соотношения y'=0 (игрек штрих равно нулю). Получаем –16х =0 (минус шестнадцать икс равно нулю), откуда находим, что х =0 (икс равен нулю).
Определим экстремум функции, для этого изобразим точку х=0 (икс равен нулю) на числовой оси и найдем знаки производной:
Из рисунка видно, что
при x<0 y´ >0, (икс меньше нуля производная положительна), т.е. функция возрастает;
при x>0, y´<0 (икс больше нуля производная отрицательна), значит, функция убывает.
Следовательно, х = 0 (икс равен нулю)– точка максимума функции, причем ymax=f(0) = =2. (игрек максимальный равен двум).
На промежутке [0, +) (от нуля до плюс бесконечности) функция убывает.
5. Составим таблицу значений функции у =(не читать) при x0 (икс больше или равен нулю):
6. Отметив найденные точки на координатной плоскости, соединив их плавной кривой и учтя при этом, что точка (0; 2) (нуль два) – точка максимума и что у=0 (игрек равен нуль) –горизонтальная асимптота, построим ветвь искомого графика при х0 (икс больше или равен нулю) (рис. 1). Добавив ветвь, симметричную построенной относительно оси у, получим весь график.
Данная кривая получила название «локон Аньези». Такое название было дано в честь замечательной женщины-математика Марии Аньези, изучавшей эту кривую.
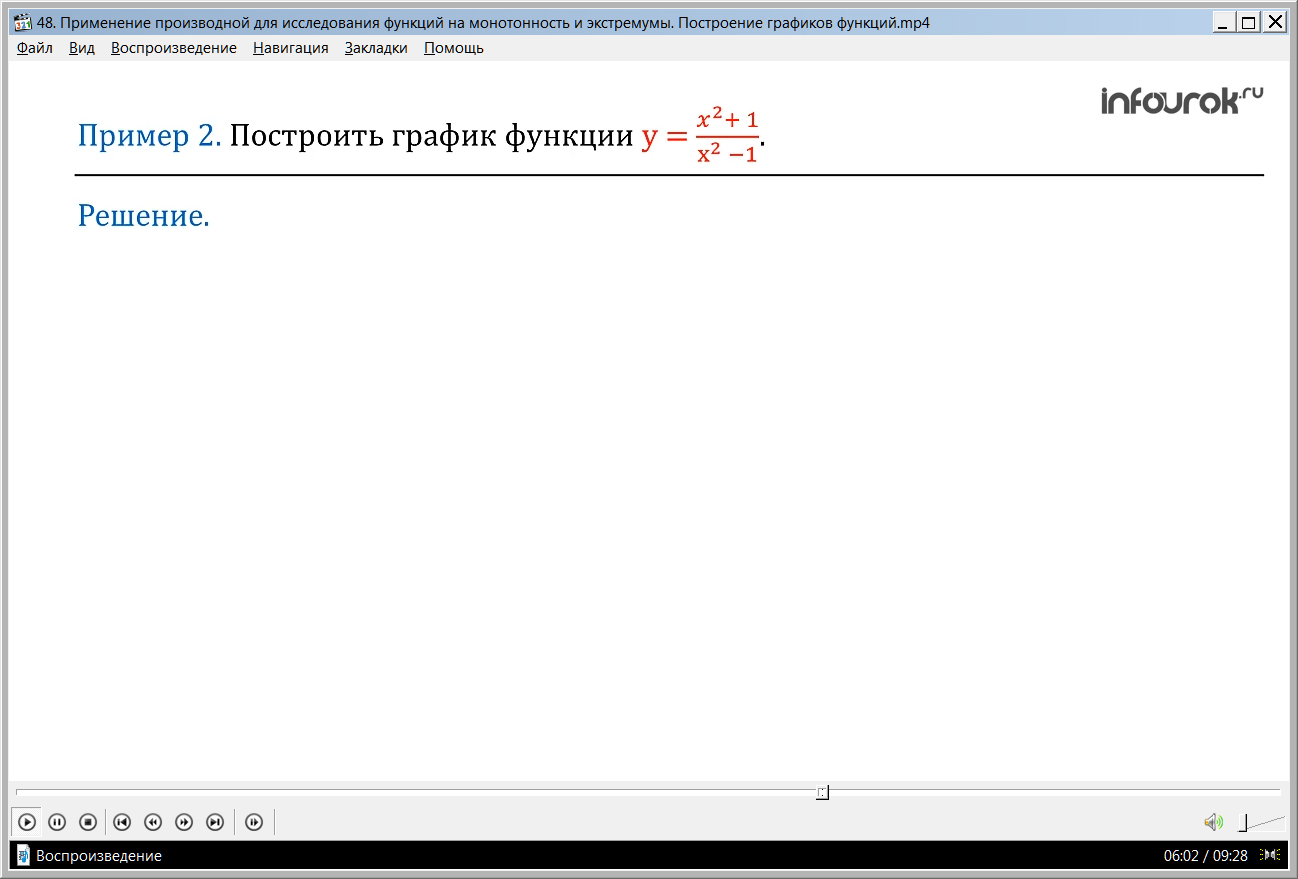
Пример 2. Построить график функции у = (игрек равный икс в квадрате плюс один, деленное на икс в квадрате минус один)
Решение.
1. Найдем область определения функции. Она задается условиями: х ≠1,х ≠–1 (икс не равен одному и минус единице) (при значениях х = 1, х = –1 знаменатель дроби обещается в нуль). Итак, D(f)= (–,–1)(–l; 1) (1;+ ) (дэ от эф равен объединению промежутков от минус бесконечности до минус одного, от минус одного до одного и от одного до плюс бесконечности)
2. Исследуем функцию на четность:
f(–x)= ==f(x). (эф от минус икс равно эф от икс)
Значит, заданная функция четна, ее график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при х 0 (икс больше или равен нуля).
3. Найдем асимптоты. Вертикальной асимптотой является прямая х = 1 (икс равен одному), так как при этом значении х (икс) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить f(x) (предел функции при стремлении икс к бесконечности).
Имеем: ===1 (предел функции икс в квадрате плюс один, деленное на икс в квадрате минус один при стремлении икс к бесконечности равен одному)
Получаем, у = 1 (игрек равен одному) – горизонтальная асимптота графика функции.
4. Найдем стационарные и критические точки, точки экстремума и промежутки монотонности функции. Имеем:
(игрек штрих равен минус два икс, деленное на квадрат разности икса в квадрате и одного).
Производная существует при любом икс из области определения функции, значит, критических точек у функции нет.
Точки максимума и минимума найдем из равенства у'=0 (игрек штрих равен нулю). Получаем –4x =0 (минус четыре икс равно нулю), откуда находим, что х = 0 (икс равен нулю).
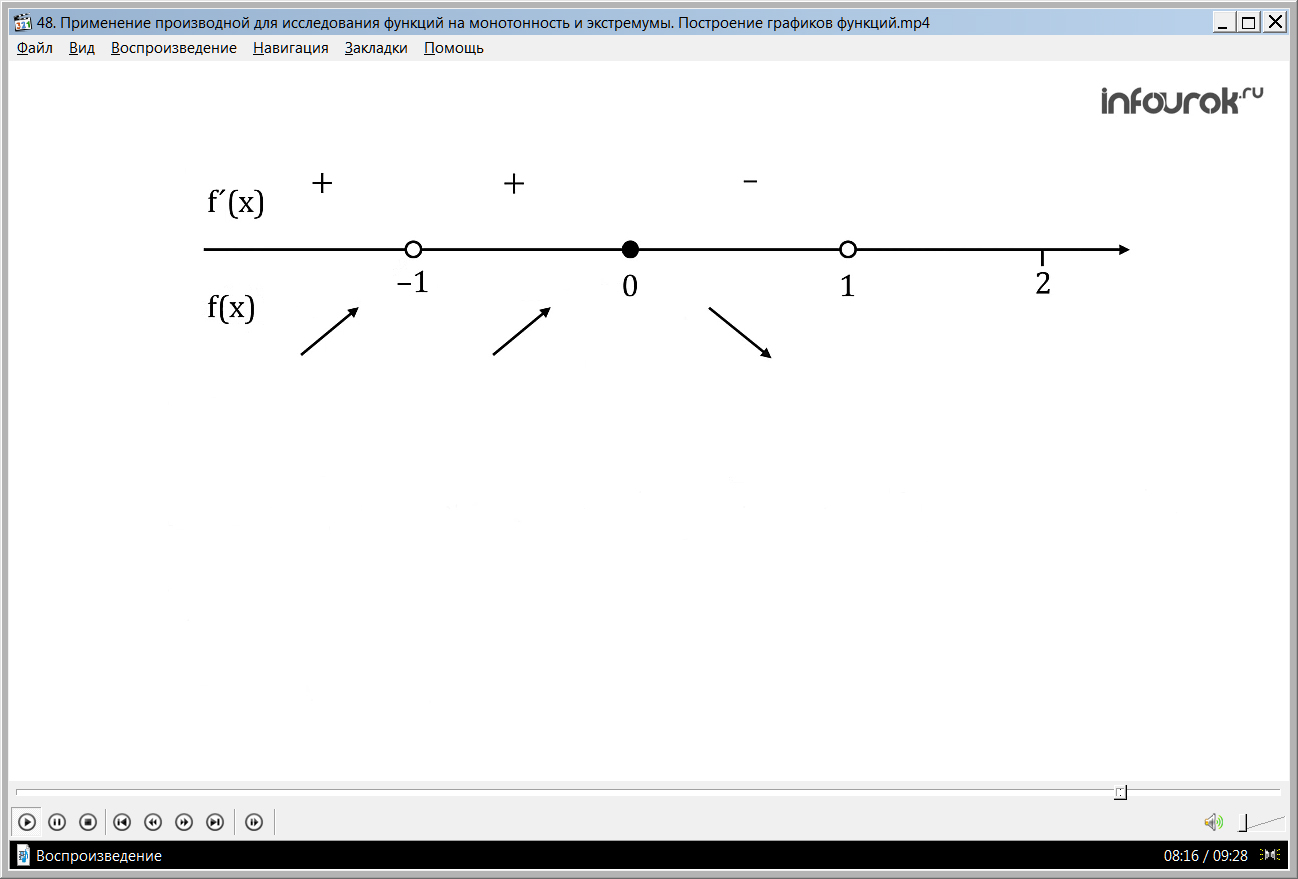
Определим экстремумы функции, для этого изобразим точки х=0 (икс равен нулю) и х = 1, х = –1 (икс равен одному и минус единице) на числовой оси и найден знаки производной:
из рисунка видно что
при х <–1, –1<x<0, имеем у'>0,
при 0<х<1, x>1, имеем у'<0. (только на экран)
Значит, х= 0 (икс равен нулю), точка максимума, причем ymax=f(0)= =–1. (игрек максимум равен минус один)
При х > 0(икс больше нуля) имеем у' < 0(игрек штрих меньше нуля), учитывая наличие точки разрыва х = 1(икс равен одному).
Получаем: на промежутке [0, 1) (от нуля до одного) функция убывает, на промежутке (1, +) (от одного до плюс бесконечности) функция также убывает.
5. Составим таблицу значений функции у = (не называть) при х 0(икс больше или равен нулю):
6. Отметив найденные точки на координатной плоскости, соединив их плавными кривыми, учтя при этом, что точка (0; –1) (нуль минус один) – точка максимума, что у = 1 (игрек равен одному) – горизонтальная асимптота, что х = 1(икс равен одному) – вертикальная асимптота, построим ветви искомого графика при х ≥0 (икс больше либо равно нуля).
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8197 |
| Номер материала | 871 |