
Урок «Примеры комбинаторных задач»

Краткое описание документа:
Видеоурок «Примеры комбинаторных задач» дает представление ученикам о задачах, в которых необходимо использовать методы комбинаторики. Видеоурок содержит материал, раскрывающий понятие комбинаторной задачи и самой комбинаторики, а также формирует умения решать такие задачи. Цель видеоурока – облегчить понимание материала, используя специальные анимационные элементы, наглядные иллюстрации, четкое структурирование решение задач с детальным описанием математическими обозначениями и голосовым сопровождением.
Приемы, используемые в видеоуроке, помогают удерживать внимание учеников на изучаемом материале, подчеркивают элементы, требующие запоминания или имеющие важное значение для усвоения материала.
Видеоурок начинается с представления темы. Дается представление о комбинаторных задачах, которые возникают при необходимости составить из конечного числа элементов различные комбинации, подсчитывать это число комбинаций. Отмечается, что также раздел математики, который изучает подобные задачи, называется комбинаторикой. Отмечается практическая ценность данной темы, так как умения производит такие вычисления, необходимы в физике, химии и других науках.
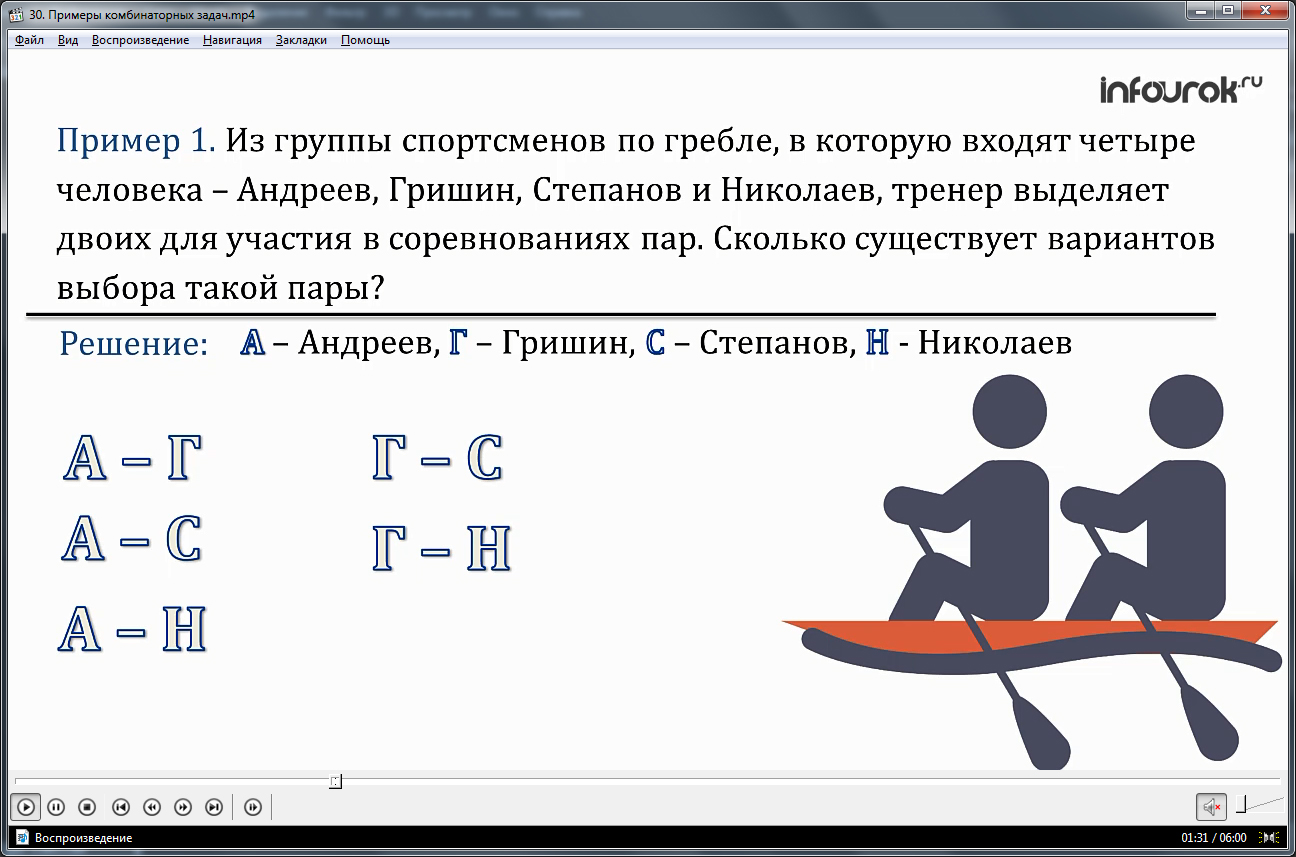
Предлагается рассмотреть решение комбинаторной задачи. А задаче необходимо выяснить, какие пары из команды 4 человек (Андреев (А), Гришин (Г), Степанов (С), Николаев (Н)) можно составить для участия в соревновании. Подсчет вариантов составления пар начинается с первого участника команды – Андреева (А). Составляются все возможные пары с его участием: АГ, АС, АН. Затем составляются возможные пары со вторым участником без первого: ГС, ГН. И остается еще одна пара СН. Очевидно, что таких пар будет 6.
После рассмотрения примера подчеркивается, что ход рассуждений, который при этом использовался, является основой метода «Перебор возможных вариантов».
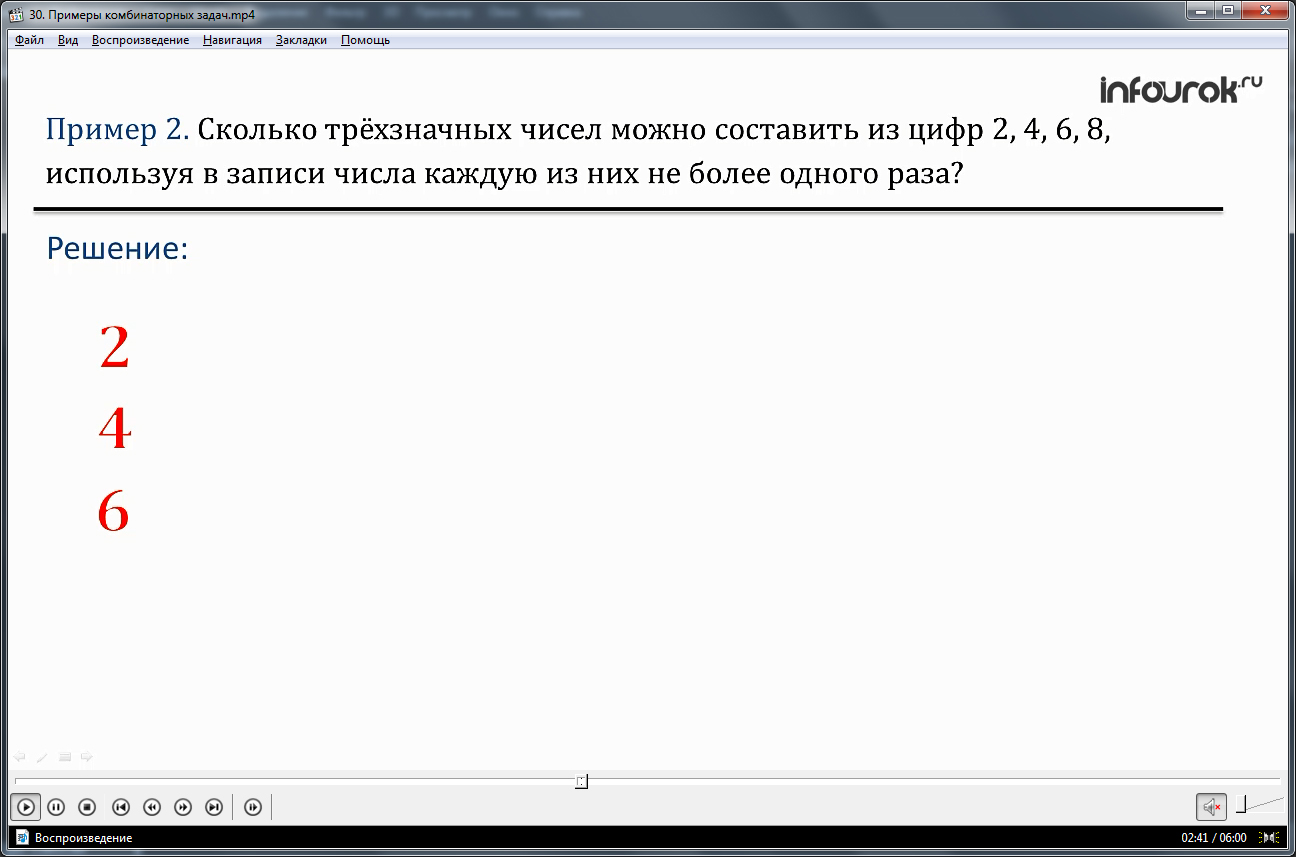
Вторая задача состоит в поиске количества трехзначных чисел, которые можно составить из цифр 2, 4, 6, 8. Составить трехзначные числа из цифр предлагается таким способом: выписываются в ряд указанные цифры. Составляя числа, на первое место выводится 2, при подстановке на второе место 4, остается за третьим – 6 и 8. Таким образом составлены первые два числа – 246 и 248. Затем подставляется на второе место 6 – с ним можно составить еще два числа 264 и 268, затем на второе место выводится 8 – составляются числа 284 и 286. Аналогично рассуждая, составляется весь ряд чисел, удовлетворяющих условиям. Записывая их в ряд возле каждой цифры, получаем набор 6 чисел с данной цифрой впереди. Всего чисел получилось 24.
Перебор вариантов для данной задачи иллюстрируется на дереве возможностей, которое демонстрируется далее. Отмечается, что решение задачи можно найти, не прибегая к выписыванию всех возможных вариантов. Для этого просто нужно учесть особенность отбора вариантов. В начале выбрать элемент можно четырьмя способами, затем следующий выбор можно сделать тремя способами, а последний – двумя. Количество возможных вариантов выбора будет произведением количества сделанных выборов: 4·3·2=24. Требуемое число найдено.
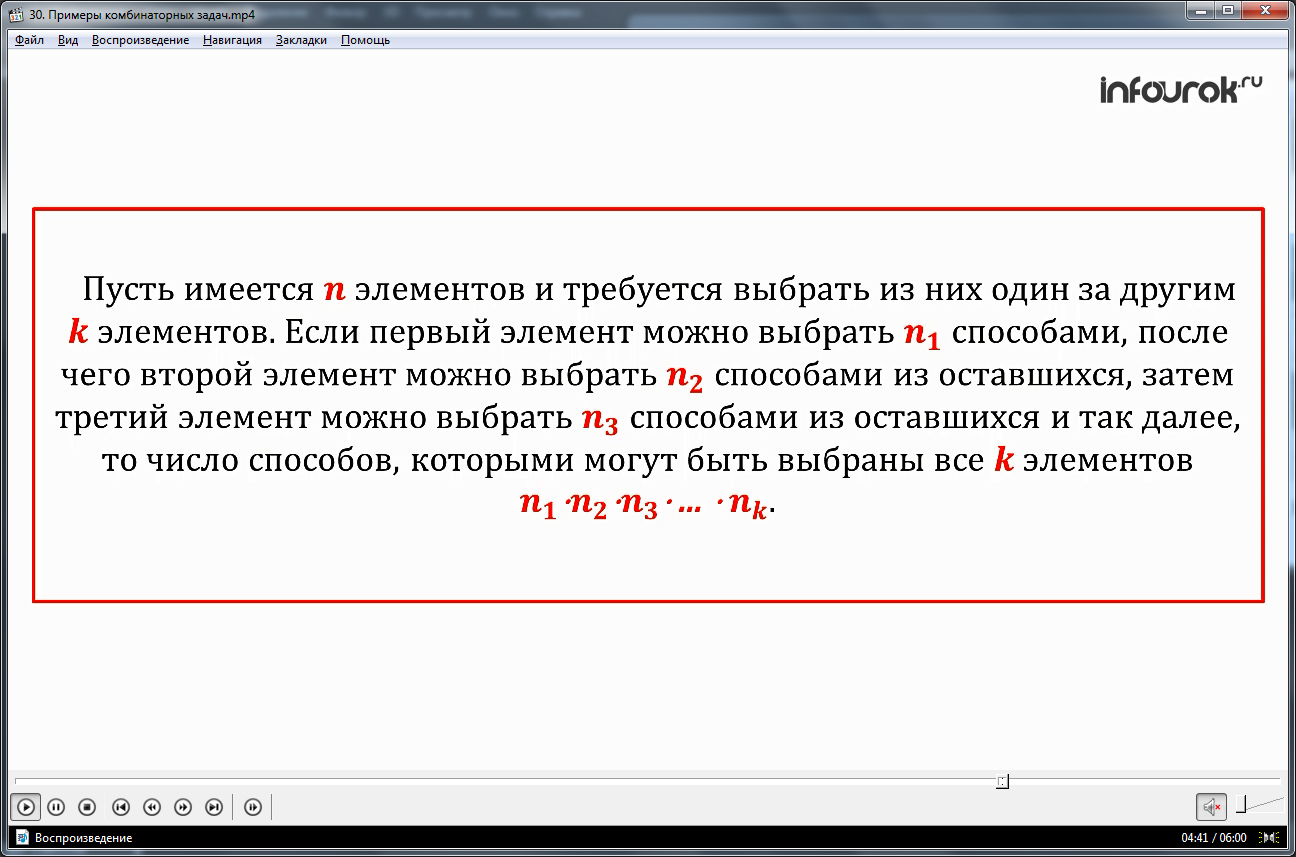
Рассмотрев на примере правило комбинаторики, далее дается его представление в общем виде. Оно утверждает, что для имеющихся n элементов, из которых выбирается k элементов, количество способов будет равно произведению n1·n2·…·nk, где n1 – количество способов, которыми можно выбрать первый элемент, n2 – количество способов, которыми можно выбрать второй элемент и т.д. до последнего k элемента.
Следующей предлагается решить задачу про туристов, которым необходимо выбрать маршрут. При этом известно, что дорог из А в В – 3, из В в С – 4 дороги, а из последнего города до пристани следуют 2 дороги. Иуристам нужно пройти все данные пункты от А до пристани. Спрашивается, сколькими способами они могут выбрать маршрут. На рисунке под задачей иллюстрируется условие задачи. Итак, первый выбор может быть сделан тремя способами, второй – четырьмя, третий – двумя. Используя изученное правило, для решения данной задачи перемножаем количество выборов, которые можно сделать: 3·4·2=24. Соответственно, количество возможных маршрутов - 24. Задача решена.
Видеоурок «Примеры комбинаторных задач»поможет учителю в объяснении учебного материала по данной теме на уроке математики в школе. Также данный материал хорошо раскрывает механизм решения комбинаторных задач, что поможет ученику самостоятельно усвоить данную тему. Также полезен материал для объяснения в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7624 |
| Номер материала | 674 |