
Урок "Призма"

Краткое описание документа:
Видеоурок «Призма» демонстрирует учебный материал по данной теме. В ходе демонстрации описывается, как образуется призма, ее свойства, виды призм. Задача данного пособия – с помощью наглядного представления материала сформировать представление у школьников о призме, ее видах и свойствах, облегчить запоминание определений и понятий, способствовать пониманию предмета изучения. Видеоматериал может применяться как наглядное пособие, сопровождающее объяснение учителя. Также видеоурок может стать полноценной самостоятельной частью урока.
Облегчить достижение целей процесса обучения помогают специальные приемы, которые используются в видеоуроках. При помощи анимационных эффектов ученикам подается хорошо структурированный материал, проводятся построения и преобразования. Чтобы легче было запомнить понятия и определения, они выделяются цветом, дополнительно озвучиваются. Применение видеоурока дает возможность повысить эффективность урока, более рационально распределить учебное время.
Видеоурок начинается с представления его названия. В начале демонстрации описывается, каким образом выполняется построение призмы. На экране изображаются две плоскости α и β, которые параллельны между собой. На α очерчивается многоугольник А1А2…An. При этом на плоскости β очерчивается равный построенному на α многоугольник В1…Вn. На рисунке для наглядности на плоскостях α и β изображены пятиугольники.
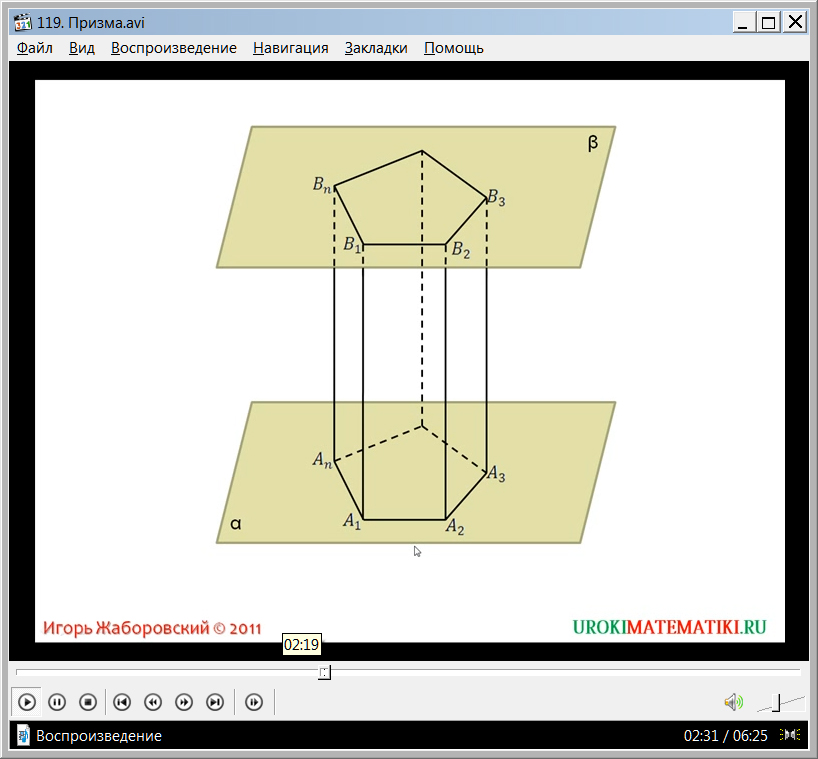
Также отмечается, что при очерчивании равного треугольника на плоскости β должно выполняться условие, что все стороны построенных многоугольников должны быть попарно параллельны. Раскрывается понятие параллельности прямых в пространстве. Оно означает, что в пространстве данные прямые лежат на одной плоскости и не пересекаются. Чтобы школьники могли представить данный факт, на рисунке изображается дополнительно плоскость, которая содержит соответствующие стороны многоугольников AnA1 и BnB1, изображенных на α и β. Прямые, содержащие данные стороны, не пересекаются, поэтому они между собой параллельны и стороны параллельны. Если условие параллельности сторон выполняется, проводятся отрезки, соединяющие соответствующие вершины многоугольников A1B1, …, AnBn. Те линии, которые не видны, отмечаются пунктиром. Таким образом, при построении мы получили n параллелограммов, составляющих боковую поверхность призмы - A1A2B2B1 и т.п. Отмечается, что признаком того, что данные стороны являются параллелограммами, есть параллельность соответствующих сторон многоугольников, построенных в плоскостях α и β, а также их равенство. Согласно сделанному построению, выводится определение n-угольной призмы как многогранника А1А2…AnВ1В2…Вn, образованного многоугольниками В1В2…Вn и А1А2…An. При этом указывается, что данные многоугольники, образующие призму, называются ее основаниями. Кроме указанных многоугольников, в состав призмы входят описанные выше параллелограммы A1A2B2B1 и т.п., образованные сторонами многоугольников и проведенными между ними отрезками. Данные параллелограммы на поверхности призмы - боковые грани. А отрезки, соединяющие между собой вершины рассматриваемых многоугольников, называют ее боковыми ребрами.
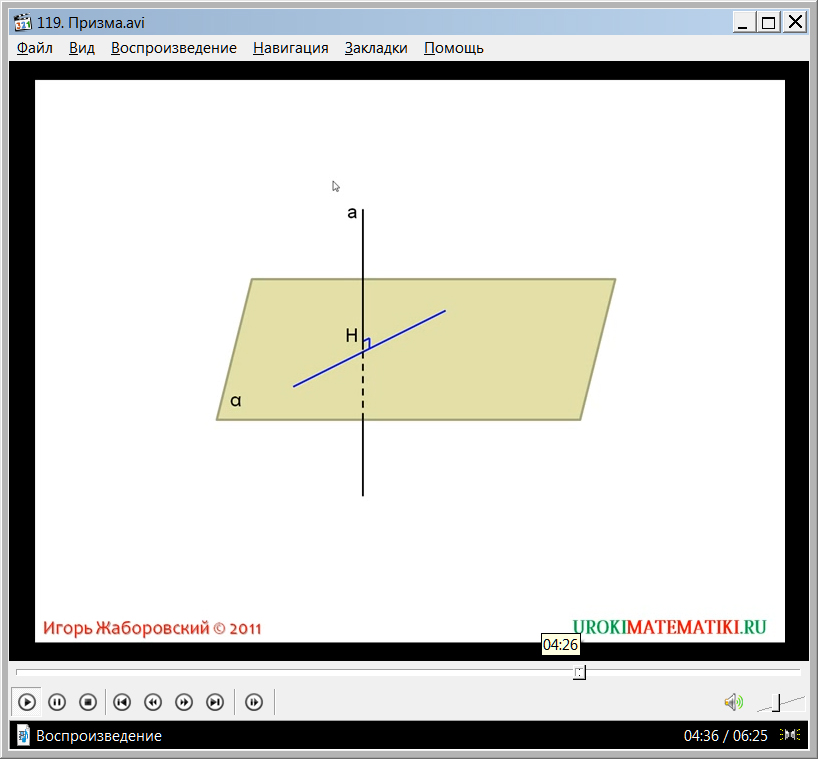
Далее рассматриваются виды призмы в зависимости от углов, который образуют с основанием его боковые грани. Чтобы рассмотреть виды призм, вводится понятие перпендикулярности прямой и плоскости. Соответствующие построения демонстрируются на рисунке. Для этого строится плоскость α и проходящая через нее прямая а. Указано, что прямая а будет считаться перпендикулярной к плоскости α, если она является перпендикулярной к всякой прямой, принадлежащей данной плоскости и проходящей через точку пересечения этой плоскости и прямой а. на рисунке продемонстрировано множество прямых, к которым является перпендикулярной прямая а. Также говорится о том, что таких прямых будет бесконечное множество. Вводится обозначение перпендикулярности прямой плоскости а ﬩α, озвучивается математически корректное описание данного факта.
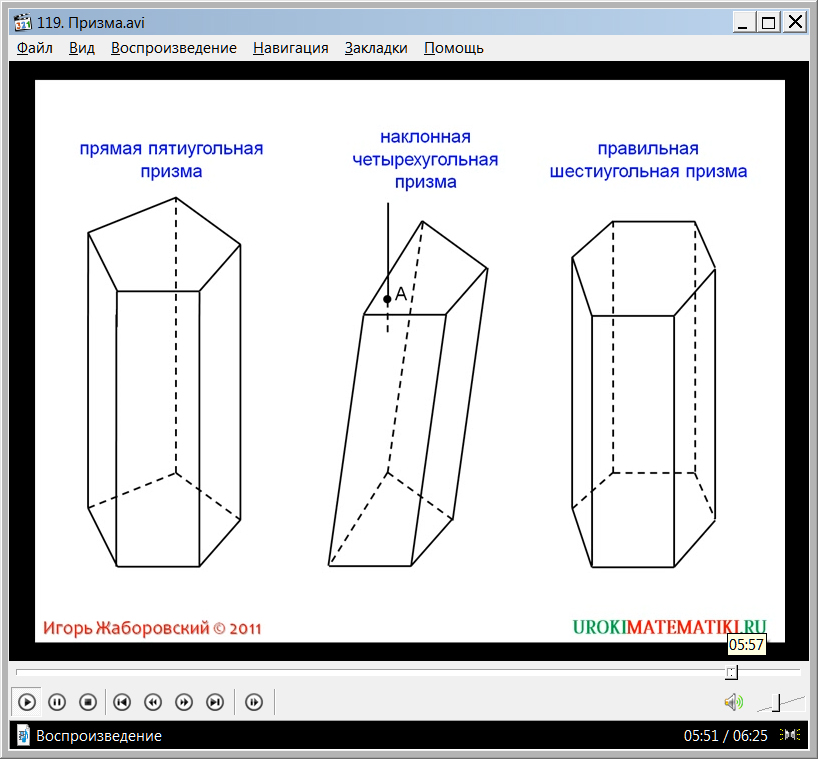
Сообщается, что прямой призма будет называться, если каждое боковое ребро расположено перпендикулярно основаниям. В качестве примера на рисунке приводится пятиугольная прямая призма. Отмечается, что данная призма считается прямой, так как ее ребра расположены перпендикулярно основаниям. Также дается определение наклонной призмы с ребрами, что не перпендикулярны плоскостям оснований. Приводится пример наклонной четырехугольной призмы. Дается определение правильной призмы. В примере изображена правильная шестиугольная призма.
Далее описываются элементы призмы. Указано, что если провести в какой-либо точке основания прямую, перпендикулярную этому основанию, то отрезок, соединяющий точки пересечения оснований с данным перпендикуляром, будет называться высотой исследуемой призмы. В четырехугольной призме на рисунке для примера изображена высота АВ. Также отмечается, что построить таких высот можно бесконечное множество, но все построенные высоты призмы равны и параллельны. Это утверждение будет доказано при изучении стереометрии в старших классах.
Видеоурок «Призма» может применяться учителем для повышения эффективности традиционного школьного урока. Наглядность материала пригодится учителю, осуществляющему дистанционное обучение. Ученикам, требующим дополнительных занятий для усвоения материала, также видеоурок поможет в изучении темы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5173 |
| Номер материала | 741 |