
Урок "Простейшие задачи в координатах"

Краткое описание документа:
Видеоурок «Простейшие задачи в координатах» является наглядным пособием для ведения урока по данной теме. Чтобы научиться решать задачи методом координат, необходимо освоить теоретические основы, а также знать и уметь применять ход рассуждения при решении задач. В ходе данного видеоурока рассматривается применение метода координат для решения некоторых типичных задач. Задача пособия – облегчить запоминание материала, его усвоение.
В видеоуроке используются методы, которые помогают воздействовать на концентрацию внимания ученика, процессы запоминания. В материале используется анимация, которая помогает структурировать и интересно представить материал. Выделение цветом помогает лучше запомнить выделенные понятия. Построения четкие и понятные, что дает возможность параллельно объяснению следить за реализацией положений на практике.
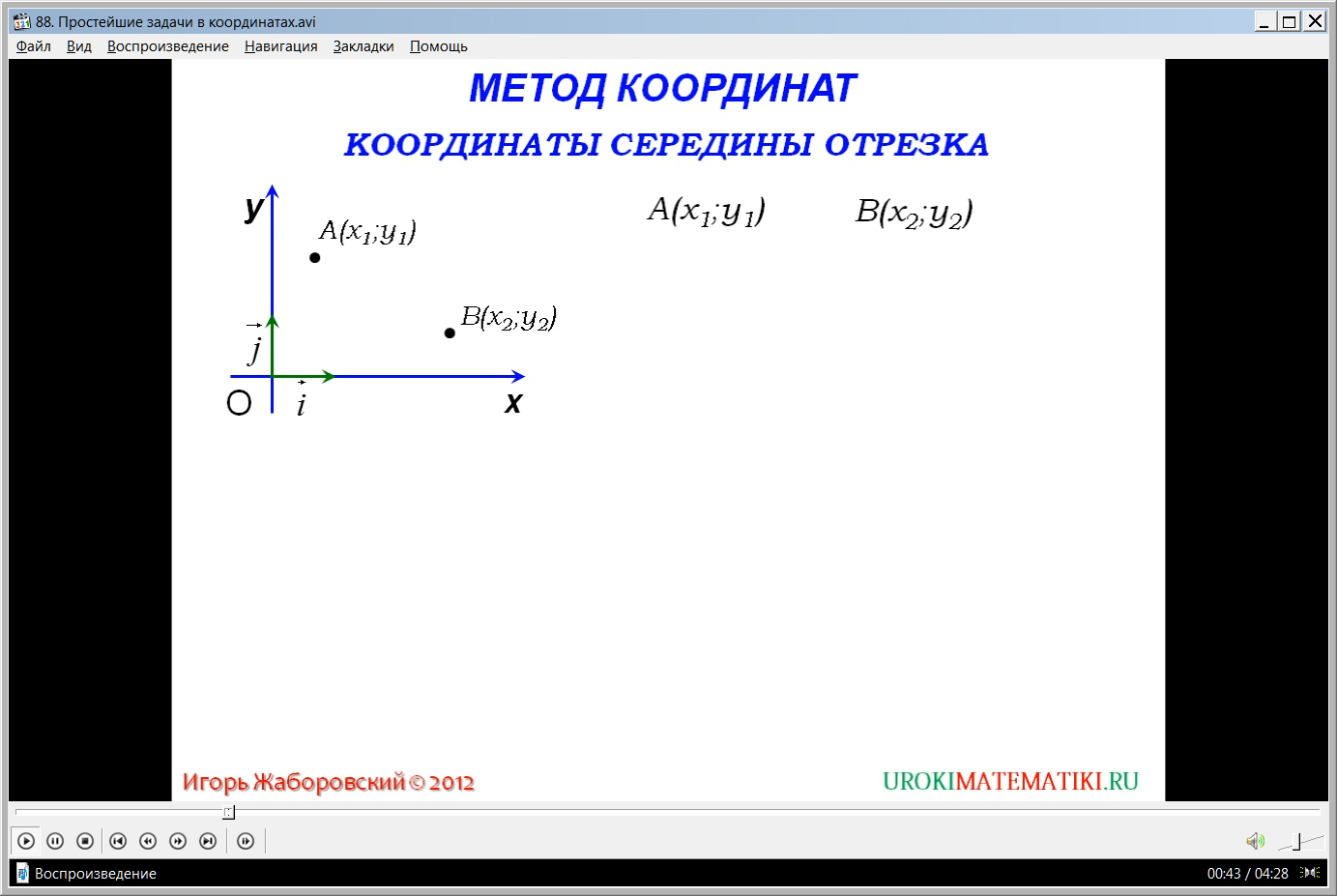
Видеоурок начинается с представления темы. Отмечаются преимущества введения системы координат, которая дает возможность исследовать свойства геометрических фигур при помощи алгебраического аппарата. Введя координаты геометрических объектов, можно исследовать их свойства при помощи уравнений, алгебраических неравенств. На экран выводится название данного метода – метод координат.
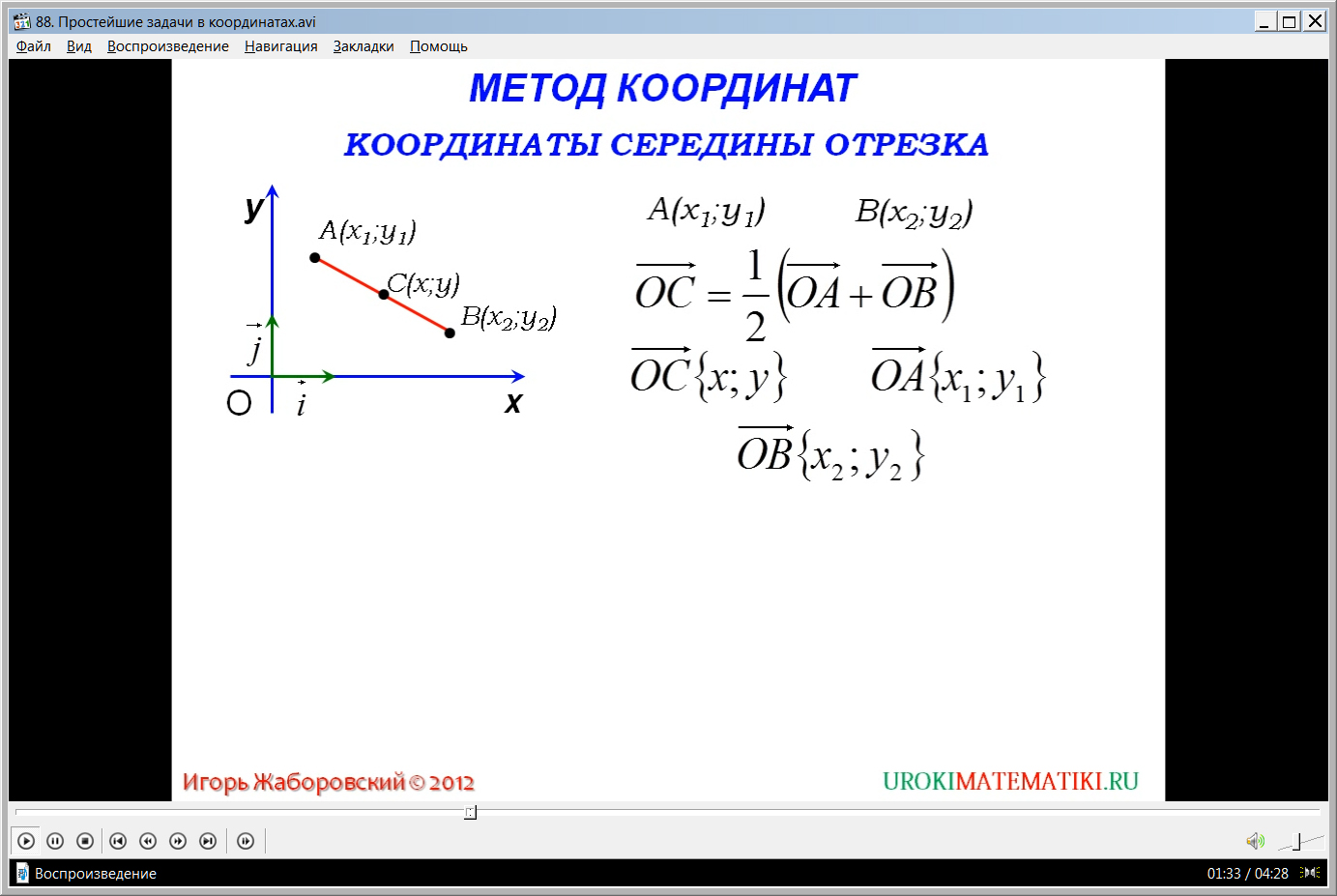
Предлагается рассмотреть три вспомогательные задачи, решение которых необходимо знать для применения метода координат. Первая задача – нахождение координат середины отрезка. Рассмотрение первой задачи начинается с построения прямоугольной системы координат ХОУ. На ней отмечены координатные векторы i¯ и j¯. На координатной плоскости отмечается точка А(х1;у1) и точка В(х2;у2). Точки соединяются в отрезок АВ. На отрезке отмечается середина С(х;у), координаты которой необходимо выразить через координаты концов отрезка. Векторное представление середины отрезка соответствует выражению ОС¯=1/2(ОА¯+ОВ¯). На основе изученного материала можно утверждать, что координаты данных векторов будут соответствовать координатам точек С, А, В. То есть ОС¯{х;у}, ОА¯{х1;у1}, ОВ¯{х2;у2}. Также зная особенности формирования координат векторов при сложении, умножении на число, получаем соответствующие координаты середины отрезка х=(х1+х2)/2, у=(у1+у2)/2. Вывод формулмруется на экране как правило, которое требует запоминания. Он гласит, что каждая координата середины отрезка равняется полусумме соответствующих координат концов.
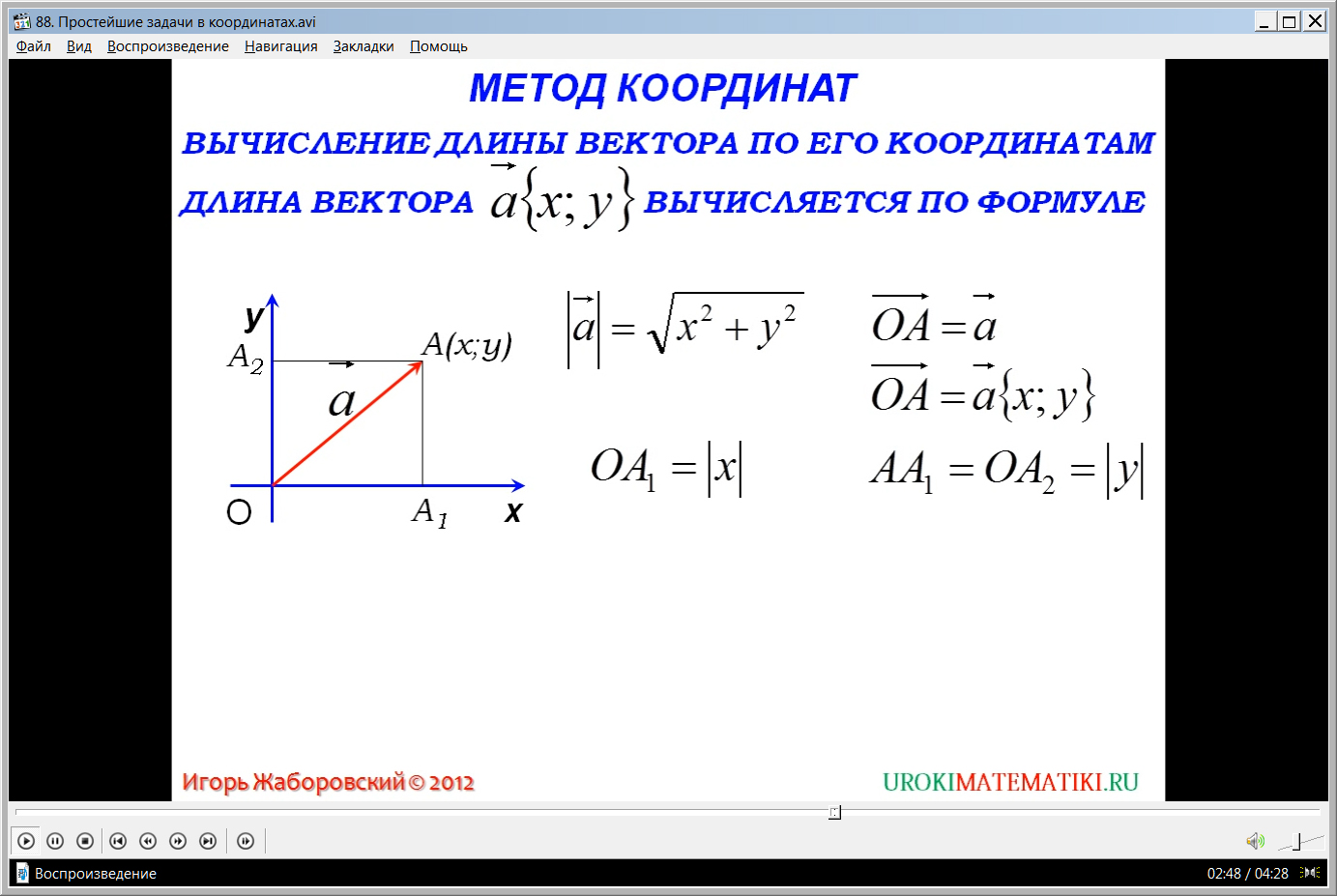
Условие второй задачи состоит в вычислении длины вектора по координатам. Необходимо доказать, что длина отрезка вычисляется по формуле |а¯|=√(х2+у2). Для доказательства проводим вектор ОА¯=а¯ и из точки А опускаем на оси координат перпендикуляры АА1 и АА2. Координаты вектора ОА¯=а¯{х;у}. Согласно построению длина отрезка ОА1=|х|, а АА1=ОА2=|у|. Получаем прямоугольный треугольник, в котором можно применить теорему Пифагора. Из нее определяем, что ОА=√(ОА12+АА12)=√(х2+у2). Известно, что длина вектора |а¯| равна длине вектора |ОА¯| и является длиной отрезка ОА. Из этого следует вывод, что |а¯|=√(х2+у2).
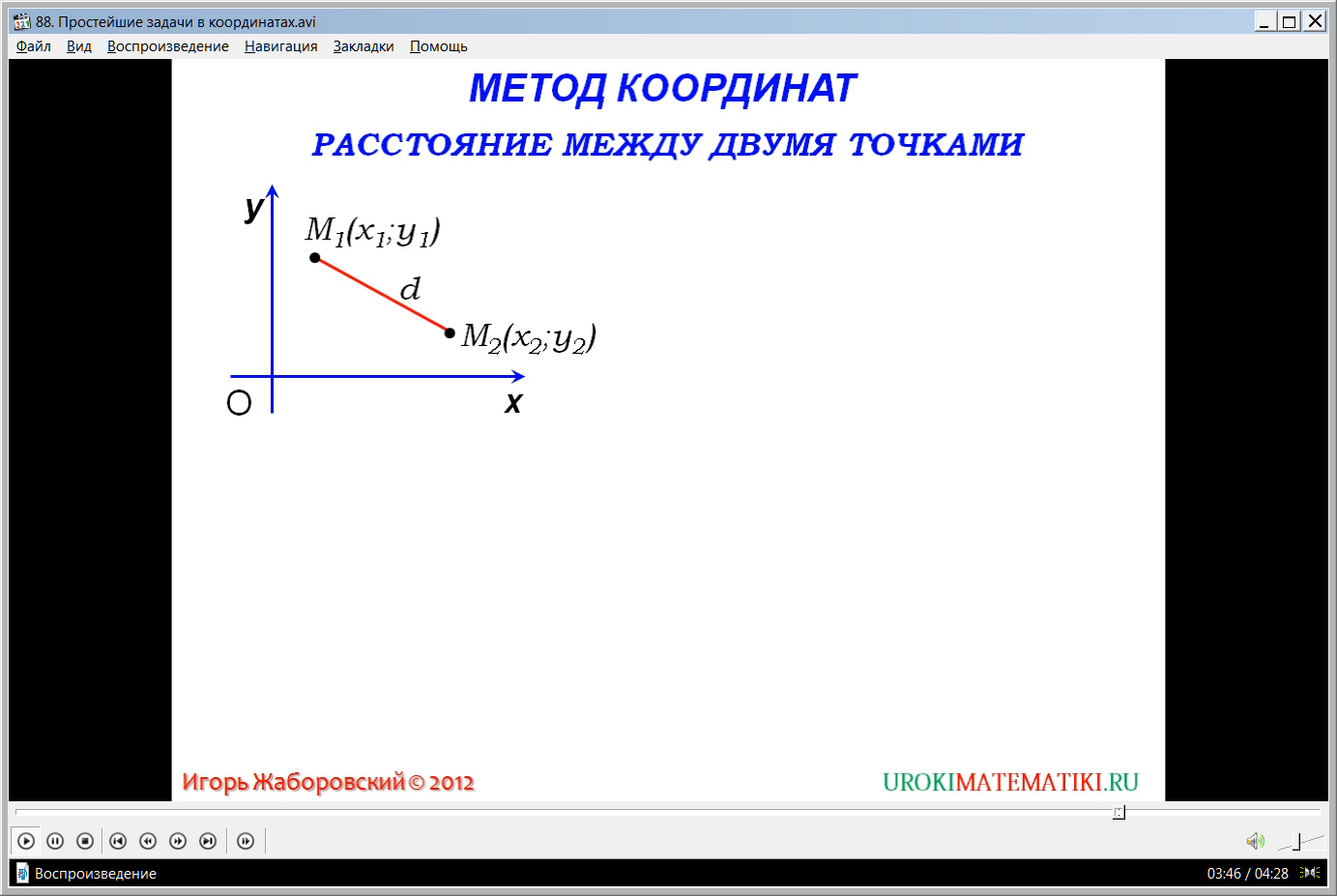
В третьей задаче рассматривается поиск алгебраического выражения для нахождения расстояния между двумя точками. Рассмотрение решения задачи начинается с построения системы координат ХОУ и выбора на координатной плоскости двух точек М1{х1;у1} и М2{х2;у2}. Необходимо выразить через координаты данных точек расстояние между ними, которое обозначается d. Из уже рассмотренной задачи по поиску длины вектора можно определить длину вектора, концами которого являются точки М1{х1;у1} и М2{х2;у2}. Длину вектора можно определить по известной формуле |М1М2¯|=√(х2-х1)2+(у2-у1)2. При этом, нужно отметить, что длина вектора |М1М2¯| равна расстоянию между точками, являющимися его концами |М1М2¯|=d. Значит, расстояние между точками в системе координат определяется при помощи формулы d=√(х2-х1)2+(у2-у1)2.
Видеоурок «Простейшие задачи в координатах» может быть использован при ведении урока в школе. Также данное пособие будет полезно учителю, выполняющему дистанционное обучение. Понятное объяснение метода решения типовых задач поможет ученику самостоятельно разобраться в их решении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6947 |
| Номер материала | 772 |