
Урок "Рациональные числа как бесконечные десятичные периодические дроби "

Краткое описание документа:
Как Вам уже известно, к рациональным числам относятся те числа, с которыми Вы работали до встречи с квадратными корнями, а именно – целые числа, десятичные и обыкновенные. На практике вы познакомитесь с единой формой записи, которую можно использовать для всех вышеперечисленных чисел.
Зачастую, при оперировании рациональными числами, пользуются десятичной формой записи, но в видеоуроке Вы сможете более детально узнать о таком виде записи как бесконечная десятичная периодическая дробь. Это актуально в силу того, что при преобразовании простой дроби в десятичную Вы можете получить как конечную, так и бесконечную десятичную дробь.
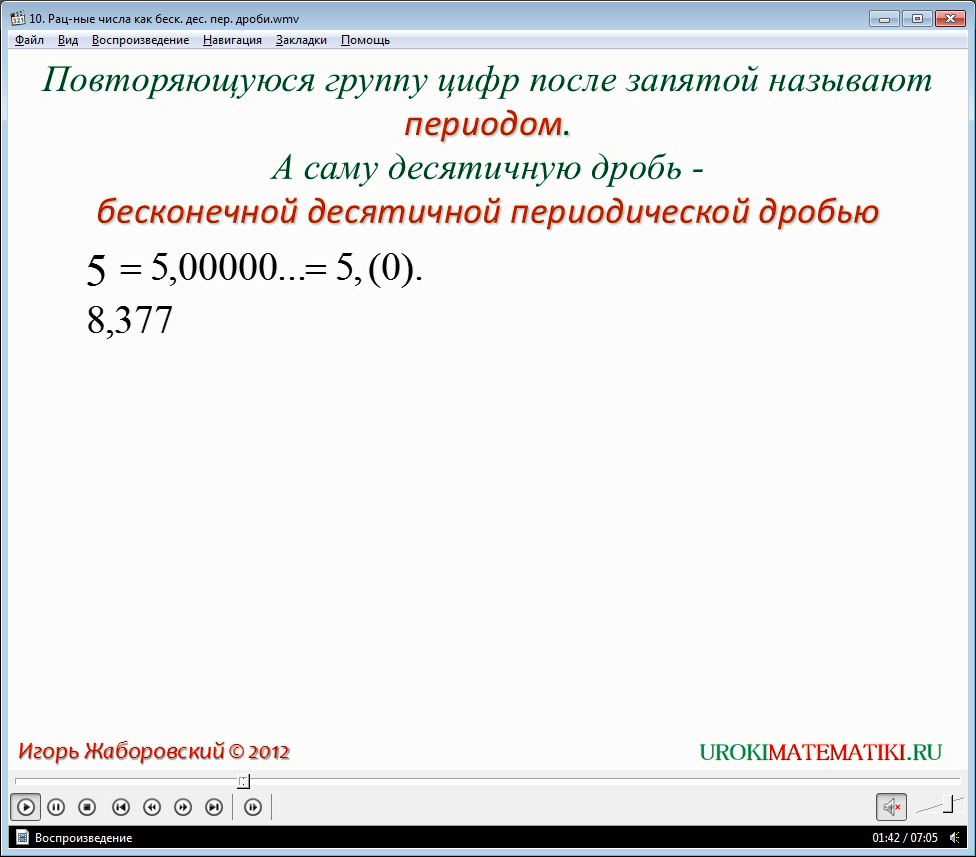
Давайте проиллюстрируем это на числах. Возьмем целое число 3, обыкновенную дробь 1/3 и десятичную дробь 6,14. Запишем целое число в виде десятичной дроби: 3,0000…. Любую конечную дробь можно рассматривать как периодическую дробь, но с периодом 0: 6,14000 … А для того, чтобы получить дробь записи m/n в десятичном виде, достаточно m разделить на n воспользовавшись методом «деления углом». В нашем случае это преобразование обыкновенной дроби при делении числителя на знаменатель «углом». В результате получим: 1/3 = 0,3333 … .
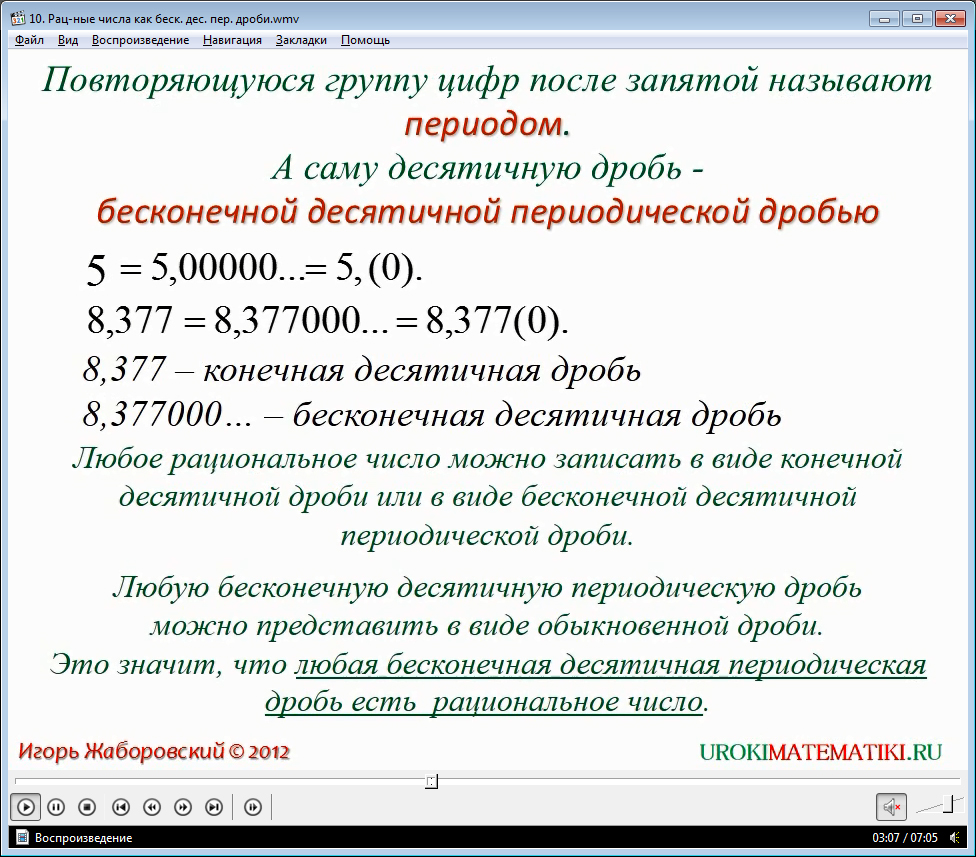
Проанализировав результат, видим, что период начинается сразу же после запятой. Так же период может начинаться после нескольких десятичных знаков, которые не входят в период. Поэтому все периодические десятичные дроби разделяют на простые и смешанные. С примером смешанной периодической дроби Вы сможете ознакомиться в видеоуроке.
Для того чтобы обозначить период, используют круглые скобки: 0, (3).

Таким образом, можно оформить какие угодно рациональные числа в виде бесконечных десятичных периодических дробей. В теоретическом аспекте этот вариант весьма удобен, а вот при решении совсем наоборот. Поскольку, когда десятичная дробь 6,14 конечного вида, то запись её в виде 6,14(0) вовсе ни к чему. Именно поэтому, как уже обуславливалось выше, существует конечная и бесконечная форма записи десятичной дроби и тем самым мы подтверждаем то, что бесконечная периодическая десятичная дробь – рациональное число.
Мы с вами просмотрели пример преобразования обыкновенной дроби в десятичную. Но также отметим, что существует алгоритм преобразования бесконечной десятичной периодической дроби в простую дробь.
Рассмотрим алгоритм преобразования бесконечной десятичной дроби в простую на следующих примерах.
Пример: преобразовать периодическую дробь 0, (36) в простую дробь.
Для этого введем следующие обозначения:
х = 0, (36) = 0,3636 …,
Помножим это соотношение на 100 и получим:
100х = 36,3636…
100х – х = 99х = 36,0000 … =36.
Итак,
х = 36/99 = 4/11.
Ответ: 0, (36) = 36/99 = 4/11.

С другими примерами Вы ознакомитесь в видеоуроке.
И так, подведем маленький вывод: множество рациональных чисел – Q, является множеством вида m/n, при этом m – целое, а n – натуральное число – множество бесконечных десятичных периодических дробей.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8576 |
| Номер материала | 534 |