
Урок "Степень с отрицательным целым показателем"

Краткое описание документа:
Прежде чем перейти к новой теме, напомним уже пройденный материал.
Степень числа а с натуральным показателем n>1 называется произведением множителей, каждый из которых равен a:an = (a*a*…a)/n
Рассмотрим выражение an более детально.
an = а – число, основание степени; n – число, показатель степени.
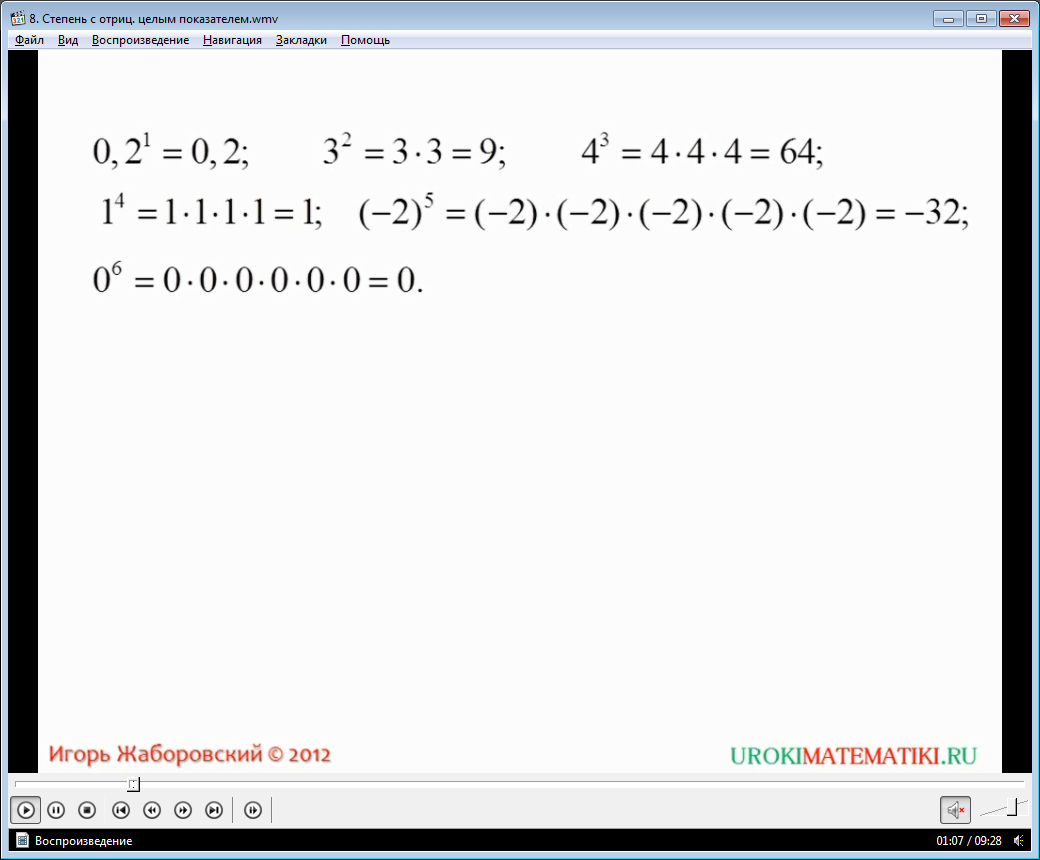
Например:
53 = 5*5*5* = 125.
Где: 5 – основание степени, 3 – показатель, 125 – значение.
Также вы знаете о понятии нулевой степени.
Степень с нулевым показателем равна 1. При а не равно 0, а0 = 1.
Например: 330 = 1; 60 =1.
Напомним основные свойства степени с натуральным показателем, основания которых равные.
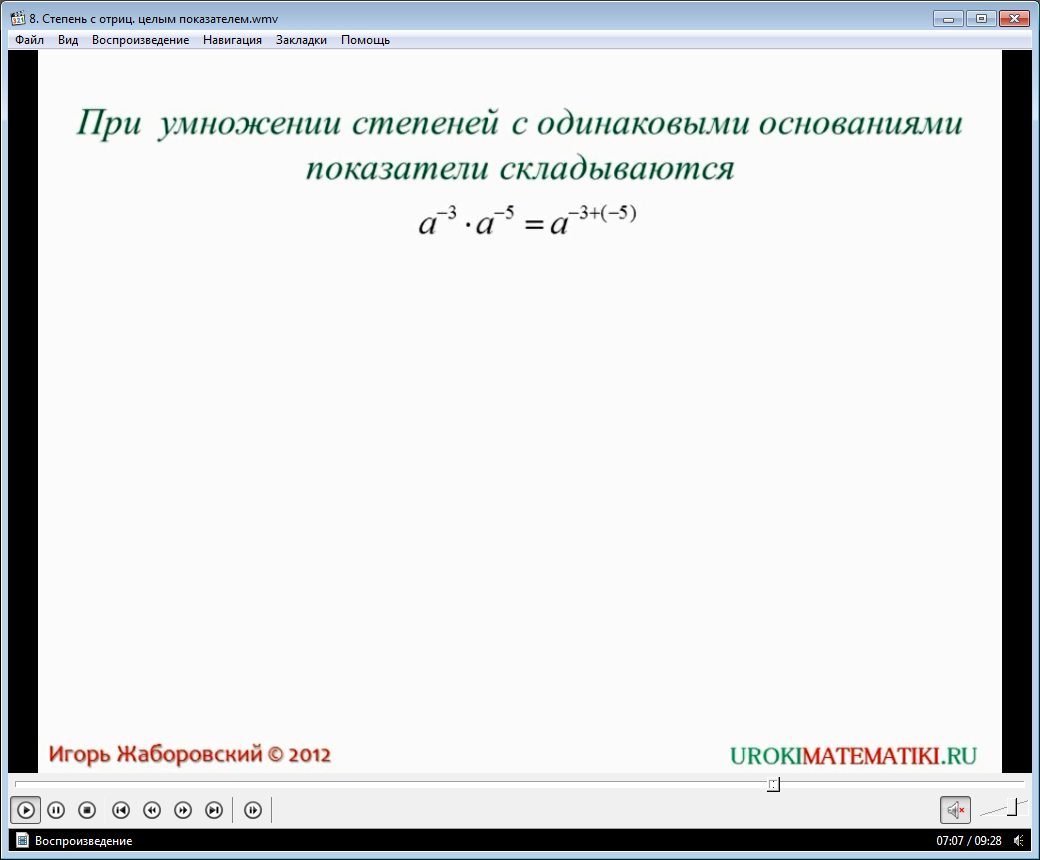
- Чтобы умножить степени с равными основаниями необходимо показатели сложить, а основание оставить без изменений.
Например: 255*253=258
- Чтобы поделить степени с равными основаниями необходимо показатели вычесть, а основание оставить без изменений.
Например: 135:133 =132.
- Чтобы возвести степень в степень необходимо перемножить показатели между собой, а основание оставить без изменений.
Например: (25)3 = 215.
- Чтобы возвести в степень произведение необходимо возвести в степень каждый из множителей.
Например: (5*17)5 = 55175
Чтобы возвести дробь в степень необходимо возвести сначала числитель, потом знаменатель дроби в эту степень.
Например: (2/3)6 = 26/36.
Повторив пройденный материал, перейдем к теме видео урока.
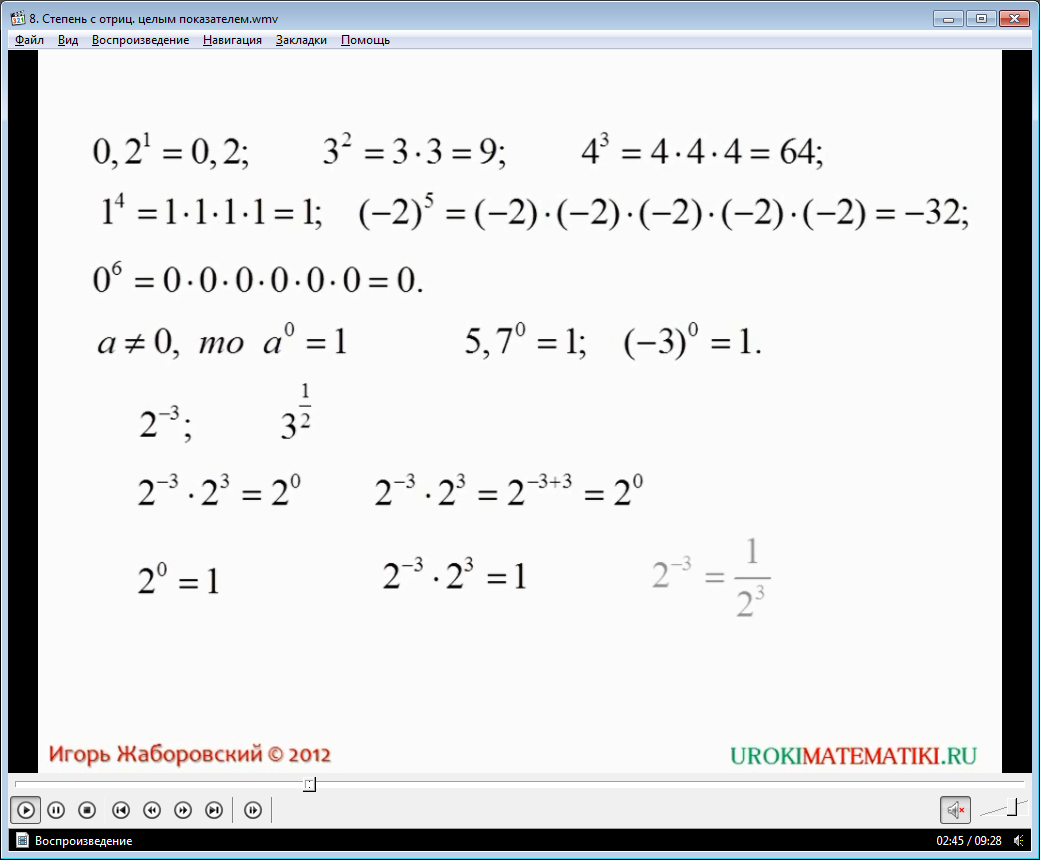
Степень числа с отрицательным показателем a-m можно подать в виде дроби a-m = 1/am того же числа с показателем, которые будет равен абсолютной величине отрицательного показателя.
Степень с отрицательным показателем наполнена таким же математическим содержанием, как и обычная, т.е. при умножении степеней с одинаковой основой, они складываются:
3-3*33 = 30
Поскольку 30 =, то из данного равенства 3-3*33 = 1 получается 3-3 = 1/33.
Из этого рассуждения и следует следующее определение:
Если m – натуральное число, и a не равно 0, то a-m = 1/am.
Например:5-7 = 1/57; 9-2 = 1/92 и т.д.
Эту формулу используют не только в таком виде. Ее еще могут использовать справа налево, если есть такая необходимость. Например:
1/3 = 3-1; 1/4 = 1/22 = 2-2
Очень важным тождеством, которое широко используют на практике, является:
(a/b)-n = (b/a)n и (1/a)-n = an при а не равно 0
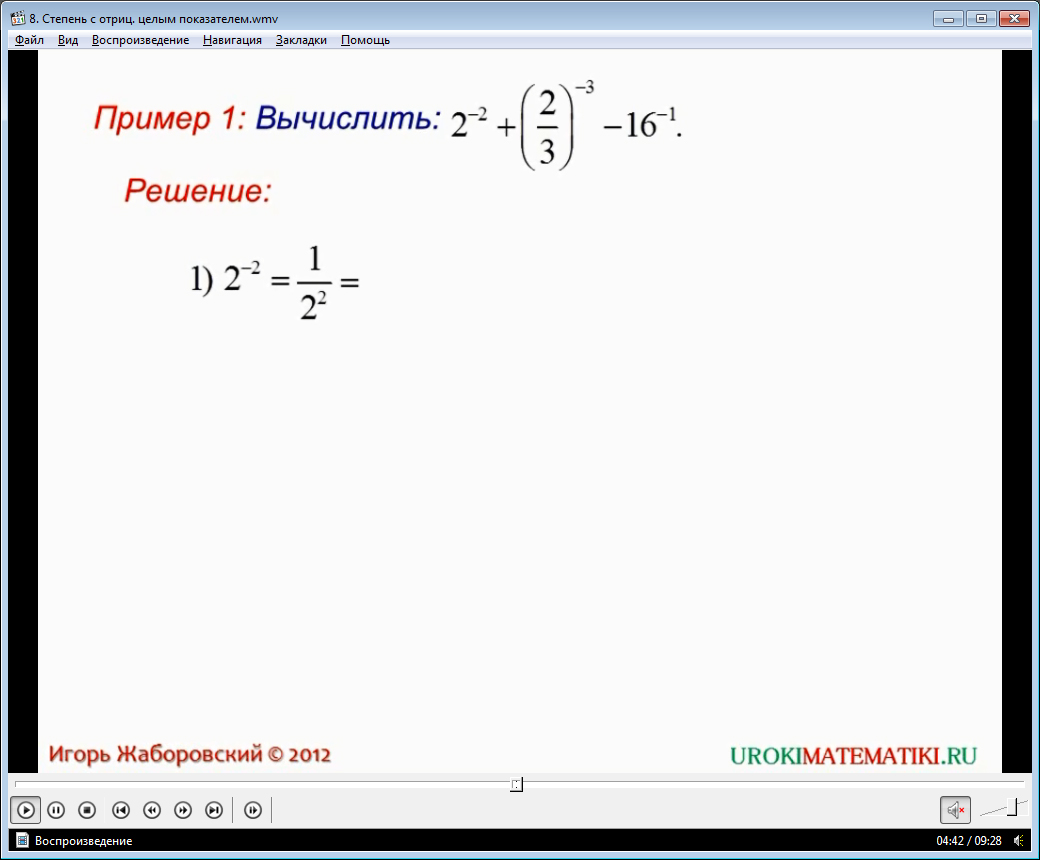
Рассмотрим пример:
(у2*у-6)/(у7*у4).
Решение:
(у2*у-6)/(у7*у4) = у2+(-6)/у-7+4 = у-4/у-3 = у-4-(-3) = у-1 = 1/у.
Более подробную информацию, а также примеры использования отрицательной степени вы можете посмотреть в видео уроке по теме.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5639 |
| Номер материала | 532 |