
Урок "Преобразование рациональных выражений"

Краткое описание документа:
Видеоурок «Преобразование рациональных выражений» - наглядное пособие для проведения итогового урока математики по соответствующей теме. В ходе демонстрации обобщаются основные методы преобразования рациональных выражений, подробно описываются примеры решения задач, в которых необходимо преобразовать выражения. Данное пособие поможет учителю повысить эффективность урока математики, подытожить множество методов преобразования, находить наиболее целесообразный способ решения математической задачи, в которой присутствуют рациональные выражения.
В видеоуроке используются методы, улучшающие запоминание материала, способствующие его пониманию. Для этого важные понятия и особенности применения методов решения заданий выделяются цветом и написанием, используются анимационные эффекты. Так как видео дополняется озвучиванием, есть возможность вставить важные комментарии. Таким образом, видеоурок становится важным инструментом наглядности и эффективным способом достижения учебных целей.
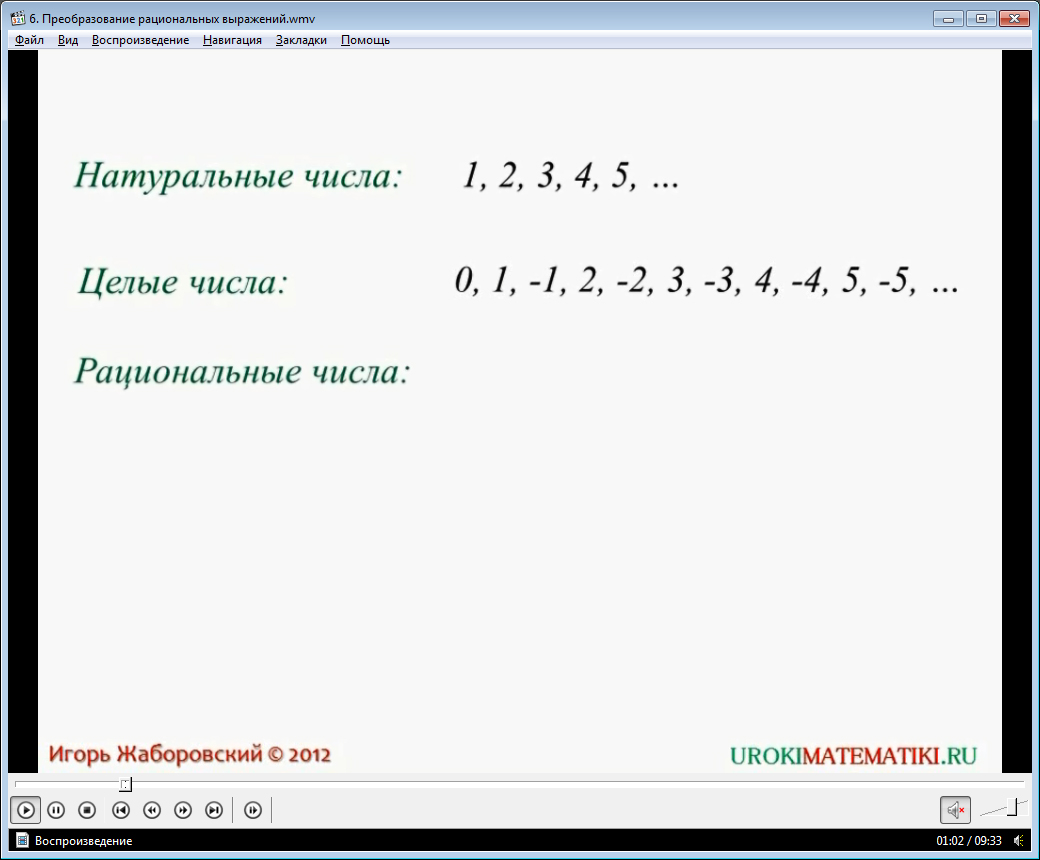
В начале урока озвучивается его название. Отмечается, что данное видео создано для итогового занятия, в котором объединяются выводы, сделанные при изучении чисел, степенях, многочленах, алгебраических степенях. В видеоуроке обобщаются сведения, полученные о математическом языке, символах.
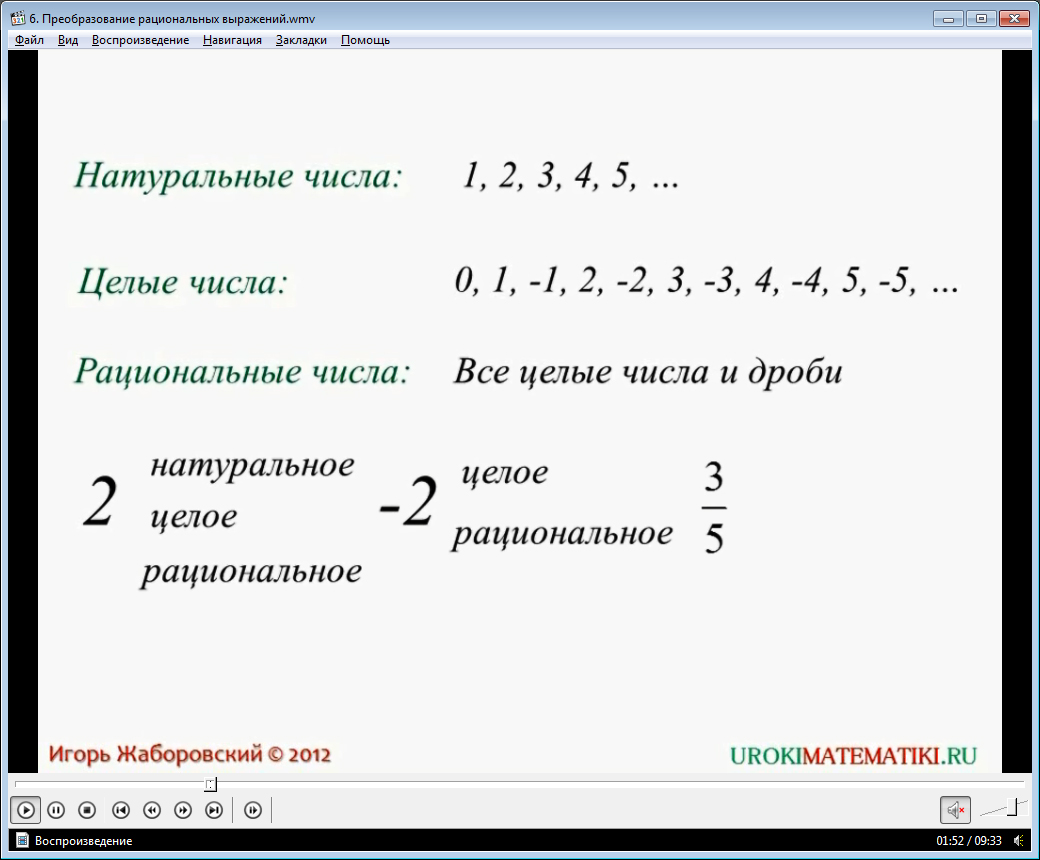
Ученикам напоминается, как расширялись их знания о числах. На экране демонстрируются виды чисел. Отмечается, что после изучения цифр, ученики познакомились с натуральными числами и правилами операций над ними. Затем раскрывалось понятие целых чисел как множества натуральных, им противоположных чисел и нуля. Затем изучались рациональные числа, в которые входят целые числа и дроби. Рассматривается пример, что число 2 является натуральным, к тому же целым и рациональным. Отмечается, что понятие рациональных чисел более широкое, а целое – уже. Самое конкретное название данного числа – натуральное. Далее указывается, что любое целое число, к примеру, -2, может быть названо целым и рациональным. Но дробь, к примеру, 3/5 является только рациональным числом.
Далее рассматривается изучение алгебраических выражений. Отмечается, что первым этапом изучения был уровень чисел, степеней и переменных. Его аналогом в изучении чисел было изучение цифр. Затем по аналогии с натуральными числами в выражениях изучались одночлены. Аналогично целым числам, изучались многочлены, и в качестве уровня рациональных чисел выступают алгебраические дроби. С помощью круговой схемы рассматривается, как расширяется понятие об алгебраических выражениях. В схеме отмечается, что числа, переменные и степени являются частным случаем одночленов, которые в свою очередь – частный случай многочленов, которые есть частью алгебраических дробей. Также указывается, что многочлен – это целое выражение, а алгебраическая дробь является дробным выражением. И любое алгебраическое выражение после преобразования может превратиться в алгебраическую дробь.

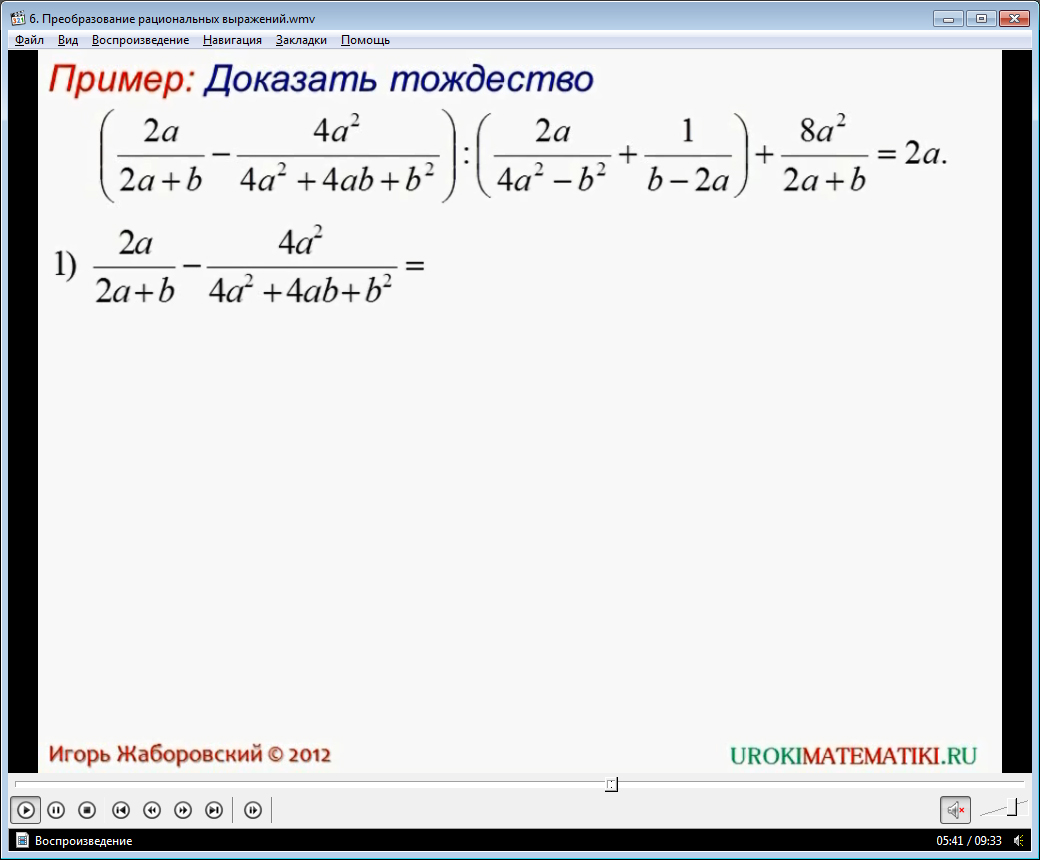
Далее рассматривается пример, в котором необходимо доказать справедливость тождества. Ученикам напоминается, что доказать тождество означает установить, что в области допустимых значений части тождества равны. Предлагается вспомнить виды преобразований, которые могут помочь доказать тождества. Это четыре метода:
- правая часть получается после преобразования левой части;
- после преобразования правой части получается левая часть;
- преобразуются обе части тождества, получая одинаковый результат;
- составляют разность частей, при этом получая нуль.
Отмечается, что при выборе способа решения задания необходимо руководствоваться видом самого выражения. В примере более целесообразным является применение первого способа. Выражение в левой части описываемого тождества очень сложное. Для его преобразования используется известное правило порядка выполнения операций – сначала преобразуется выражение в скобках, затем операции умножения, деления, а затем сложения и вычитания. Далее описываются действия, которые нужно выполнить для решения задания. Сначала преобразуется выражение в скобках – две алгебраических дроби приводятся к общему знаменателю, после чего выполняется вычитание. Аналогично выполняется сложение алгебраических дробей с разными знаменателями в других скобках. Далее осуществляется деление дробей, полученных в итоге преобразования выражения в скобках. Четвертым действием является сложение дробей с равными знаменателями. В результате преобразований получается выражение, равное выражению из правой части. Таким образом, данное тождество считается верным. При этом уточняется область допустимых значений, при которых тождество верно. Такими значениями для пары a, b будут все рациональные числа, кроме обращающих знаменатели исходных дробей в нуль. Соответственно, недопустимы равенства 2a-b=0, 2a+b=0, b=0.
Видеоурок «Преобразование рациональных выражений» поможет сформировать умение преобразовывать рациональные выражения на традиционном уроке математики в школе. Также данный материал может быть полезен учителю для ведения дистанционных уроков. Ученикам, которые требуют дополнительных занятий, чтобы освоить тему, пособие может быть рекомендовано для самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4583 |
| Номер материала | 530 |